
Support Vector Machines Math Intuitions
Last Updated on November 3, 2024 by Editorial Team
Author(s): Fernando Guzman
Originally published on Towards AI.
Support Vector Machines, or SVM, is a machine learning algorithm that, in its original form, is utilized for binary classification.
The SVM model seeks to determine the optimal separation line between two classes, understood as the best margin between these classes, as demonstrated in the following example:

As shown in the image, we have a separation line which, in a multidimensional space scenario, is a hyperplane. The dots closest to the separation line are the support vectors that help define the best separation line.
MARGIN
Before delving into the model, it is essential to understand the concept of margin, which comprises the dividing hyperplane together with the support vector lines. Therefore, the margin represents the distance between the two classes. Let us examine the following illustration:

As you can see, the margin is the distance D between two classes. To deduce the margin, let us examine the following illustration:

Here, Xn represents the given answer, and d is vector that represents the distance between the hyperplane and the answer. This vector is orthogonal to the hyperplane. w denotes the weight, and X0 is any point on the hyperplane. Consequently, r is the vector that reflects the distance between this point and the answer.
In SVM, the objective is to maximize the distance of all the support vectors. Based on the previous illustration, we can now comprehend the distance between the hyperplane and the answer as expressed by the following equation:

From the last illustration we can also understand r is the following:

Applying the distributive property, we get:

Now, we add the bias to the equation:

As illustrated, the first part of the numerator represents the prediction equation, while the second part is the null vector, which we assume to be zero. The prediction yields only two possible outputs: 1 and -1. However, considering the absolute value, the equation is reformulated as follows:
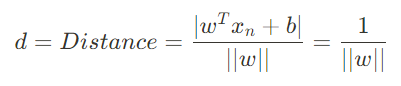
This final equation represents the distance between the hyperplane and the answer. However, the answer can occur on either side of the hyperplane. Thus, we postulate that the margin is as follows:

ORIGINAL SVM (Hard SVM)
In its original form, the SVM was developed to address binary classification problems. This version presupposes that all data points are correctly classified and are linearly separable.
Primal Problem
The primal problem of SVM consists of maximizing the distance expression, which ultimately leads to minimizing the regularization term. The primal problem of SVM is represented by the following equation, which serves as our objective function, also known as the Hinge Loss:

As observed in other models, our prediction is derived from the same formula, which is:

Given that we are addressing a binary problem, it can be assumed that our prediction will yield only two possible outputs:

The primal problem involves minimizing the regularization term, subject to the following constraints:
- Classification must be correct
- Prediction and answer must coincide in sign; thus, the following condition is required:

Keeping these conditions in mind, we apply Lagrange Multipliers to each prediction in our dataset to derive the objective function as follows:

This is a restrictive optimization expression and can be resumed as follow:

This final expression represents the objective function of the primal problem, also known as hinge loss. This expression is subject to the restriction that any Lagrange multiplier must be equal to or greater than zero.
Note that this objective function depends on three parameters: weights, bias, and Lagrange multipliers. Consequently, it entails multiple constraints, making it challenging to analyze.
Dual Problem
Given the multiple constraints of the primal problem, a mathematical technique is required to reformulate this expression to depend solely on the Lagrange multipliers. This is achieved through the dual problem, which simplifies the primal problem to depend on only one parameter and transforms it into a maximization problem.
To derive the objective function of the dual problem, it is necessary to get the derivative of the primal problem with respect to the parameters and the bias:


Finally, we regard our primal function as the third equation. We then substitute equations №1 and №2 into №3, resulting in the following expression:

Replace wT with equation №1, and we obtain the following:

Both of the double sums are similar terms thus we can multiply them by -1 to arrive at the following expression:

This is the objective function of the dual problem and is a quadratic problem.
SOFT SVM
This version of the SVM admits outliers, implying a permissible range of misclassification. Given this scenario, we will now assign an epsilon value to each of our predictions; consequently, the condition for the main operation alters to:

Here, C represents a hyperparameter defined by us that determines the tolerance range for misclassification within the model. As C increases, epsilon ϵ decreases because the allowable error range becomes broader, and vice versa.
Also, our prediction restriction will change to the following:

Primal Problem
Considering the mentioned changes, our primal problem will change as follows:

In this expression, mu μ also functions as a Lagrange multiplier for epsilon ϵ.
Dual Problem
For the dual problem, the derivatives will be the following:



Here, an additional equation is presented, which is the derivative of the primal problem with respect to epsilon ϵ.
Following the same process as in the hard SVM, we substitute these derivatives into the primal problem equation, yielding the dual problem:

Note that the variation in the final terms is the addition of a kernel.
MULTICLASS SVM
Originally, SVMs were used for binary classification; however, an extension exists that enables multiclass classification, which is available in two versions:
V1: ONE vs All
This version involves comparing one class against all others to define classes or make classifications, as illustrated in the following example:

As you can observe, this approach trains an SVM for each class. A limitation of this type of SVM is that it may result in regions without classification.
V2: ONE vs ONE
This version consists of making comparisons between one class and another to define classes, as demonstrated in the following example:

This version trains an SVM for each pair of classes and then compares the results to deliver a prediction.
REGRESSION SVM
Originally, SVMs were primarily used for classification problems, but they can also be adapted to handle regression problems.
As for regression SVM, we make the follow:

The data must be contained within the margin, and our objective function will be derived by additionally minimizing the regularization term given by:

And our constrain or restrictions will be as follows:

KERNEL METHODS
Also known as kernel tricks, this technique enables the transformation of a non-linearly separable dataset into one that is linearly separable. Essentially, kernels are functions applied to the dataset to increase its dimensionality.
The most used kernels are the following:


Other common kernel functions are these:
- Polynomial Kernel
- Gaussian Kernel
- Sigmoid Kernel
CONCLUSION
Now, we have all the elements needed to implement SVM. Keep in mind that the most commonly used SVM models are Soft and multiclass SVM. To implement an SVM model, you only need to follow the steps for training a model as with any ML model, but using the formulas we have derived here. I hope this was helpful for understanding the SVM algorithm.
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














