ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting

Author(s): Reza Yazdanfar

Originally published on Towards AI.

ATFNet is a deep learning model that combines time and frequency domain modules to capture dependencies in time series data. It introduces a novel weighting mechanism to adjust weights based on periodicity, enhances the Discrete Fourier Transform, and includes a Complex-valued Spectrum Attention mechanism for intricate relationship discernment, and of course, outperforming current methods in long-term time series forecasting (This is the fixed part of any new paper, I mean being better than others😂).

Oh dear, it sounds a lot!! (at least to myself) But don’t worry I’m going to break it down into digestible😉

The challenge of Time Series data:

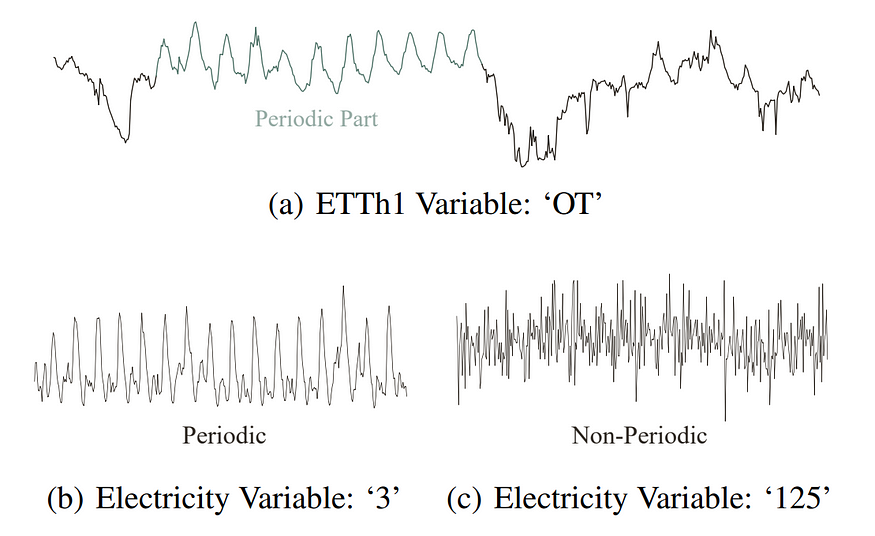
One of the challenges with time series comes from two concepts: periodicity and non-periodicity.

Periodicity means that at any given time, the value is dependent on a certain data point at a certain time ago and is more global, while the latter is about the dependency with the near data point and is more local. Taking both into account when it comes to time-series forecasting is challenging.

Also, there are two types of domain for time series (TS) analysis, namely time domain and frequency.

The time domain is about changes in the intensity of a signal as time progresses while the frequency domain analyzes time series from the frequency perspective.

The first one helps to understand local dependencies and the latter global dependencies.

Mixing both is a great approach but needs to get done efficiently unless we cannot take advantage of both at the same time.

ATFNet framework (the proposed model here) aims to address the challenge of dealing with the mixing of distinct periodic properties in real-world time series data. This combination allows for a comprehensive analysis that leverages the strengths of both the time and frequency domain representations.

ATFNet is mainly composed of three sub-parts:

1. T-Block to capture local dependency from the time domain.
2. F-Block to capture global dependency from the frequency domain. The Extended DFT is used to generate a frequency-aligned spectrum of input series.
3. The Dominant Harmonic Series Energy Weighting allocates appropriate weights for F-Block and T-Block according to the periodic property of the input series.

Seems a lot, doesn’t it?

Well let’s break it down to understand it better 😉

Extended DFT:

Here we use Extended DFT in ATFNet to align the frequency spectrum of the input series, allowing for a more comprehensive analysis of the time series data. We decrease the cost by considering just the first half of the output (the second is removed).

DFT basis of the complete series is as follows:

In this way, we achieve a spectrum of length L + T that aligns with the DFT spectrum of the complete series.

Now, let’s dive in the model architecture🫡

Architecture in general:

1. T-Block
2. F-Block
3. The Dominant Harmonic Series Energy Weighting

In general, the input goes in two directions, firstly T-Block, and secondly Extended DFT and then F-Block.

F-Block

Note that F-Block is based on the original attention (attention is all you need) with a bit of modification. In a nutshell, the attention mechanism is the next level of neural network, routing everything to everything to learn and generalize on the data. It’s not efficient but powerful, though there are lots of modifications to make it more efficient.

This block takes in F, a univariate spectrum (the output of Extended DFT) with the length of L. Then we normalize F for RevIN method to handle frequency domain spectra (we denormalize them at the end).

Then the final output of Complex-valued Spectrum Attention is calculated as follows:

Reversible Instance Normalization (RevIN), is a normalization-and-denormalization method with learnable affine transformation. RevIN can be applied to any deep neural network, being a model-agnostic method.

Note that the positional embedding is disabled here (not used).

T-Block

This part is responsible for the local dependency of the data, in other words, the time domain. The data is patched into N smaller patches with the sequence length of P. We embed each small patch into the encoder transformer and at the end we use a linear projection to generate the output. Note that RevIN is used here as well (for distribution shift).

Dominant Harmonic Series Energy Weighting

The Dominant Harmonic Series Energy Weighting mechanism dynamically adjusts the weights between the time and frequency domain modules based on the periodic property of the input series

Results:

It’s part of any paper to say that we’re the best, and this paper is not and exception here😅

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI