
Naive Bayes Classifiers
Last Updated on July 24, 2023 by Editorial Team
Author(s): Bindhu Balu
Originally published on Towards AI.
This article discusses the theory behind the Naive Bayes classifiers and their implementation.
Naive Bayes classifiers are a collection of classification algorithms based on Bayes’ Theorem. It is not a single algorithm, but a family of algorithms where all of them share a common principle, i.e., every pair of features being classified is independent of each other.
To start with, let us consider a dataset.
Consider a fictional dataset that describes the weather conditions for playing a game of golf. Given the weather conditions, each tuple classifies the conditions as fit(“Yes”) or unfit(“No”) for playing golf.
Here is a tabular representation of our dataset.

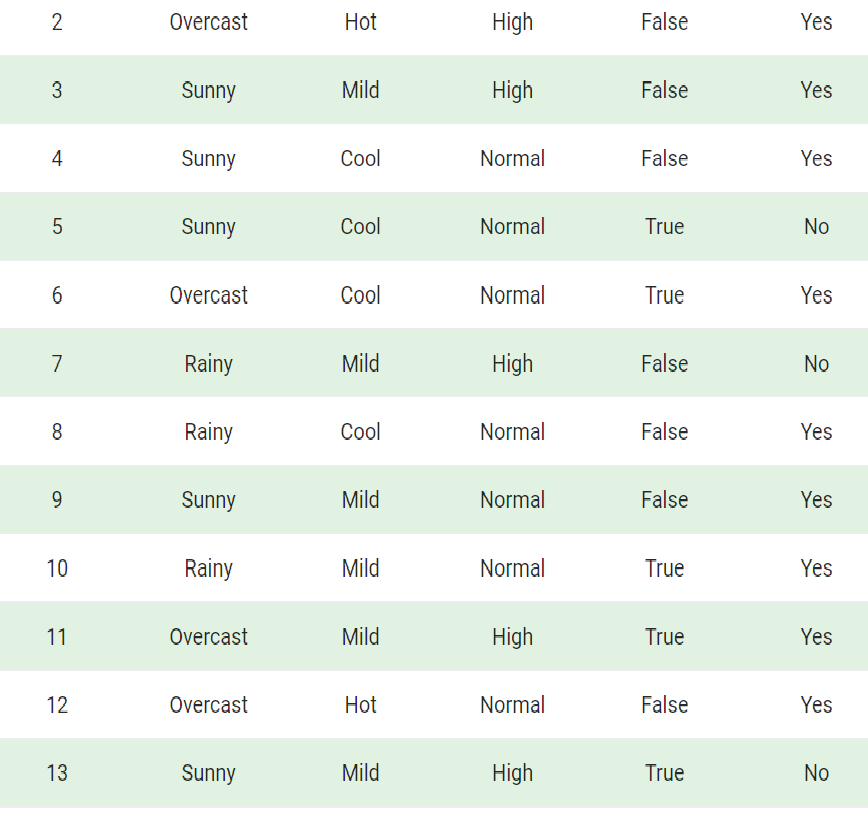
The dataset is divided into two parts, namely, feature matrix and the response vector.
- The feature matrix contains all the vectors(rows) of the dataset in which each vector consists of the value of dependent features. In the above dataset, features are ‘Outlook,’ ‘Temperature,’ ‘Humidity,’ and ‘Windy.’
- The response vector contains the value of the class variable(prediction or output) for each row of the feature matrix. In the above dataset, the class variable name is ‘Play golf.’
Assumption:
The fundamental Naive Bayes assumption is that each feature makes an:
- independent
- equal
contribution to the outcome.
With relation to our dataset, this concept can be understood as:
- We assume that no pair of features are dependent. For example, the temperature being ‘Hot’ has nothing to do with the humidity, or the outlook being ‘Rainy’ has no effect on the winds. Hence, the features are assumed to be independent.
- Secondly, each feature is given the same weight(or importance). For example, knowing the only temperature and humidity alone can’t predict the outcome accurately. None of the attributes is irrelevant and assumed to be contributing equally to the outcome.
Note: The assumptions made by Naive Bayes are not generally correct in real-world situations. The independence assumption is never correct but often works well in practice.
Now, before moving to the formula for Naive Bayes, it is important to know about Bayes’ theorem.
Bayes’ theorem finds the probability of an event occurring given the probability of another event that has already occurred. Bayes’ theorem is stated mathematically as the following equation:

where A and B are events and P(B)? 0.
- We are trying to find probability of event A, given the event B is true. Event B is also termed as evidence.
- P(A) is the priority of A (the prior probability, i.e., probability of an event before evidence is seen). The evidence is an attribute value of an unknown instance(here, it is event B).
- P(AU+007CB) is a posteriori probability of B, i.e., probability of event after evidence is seen.
Now, with regards to our dataset, we can apply Bayes’ theorem in the following way:

where y is class variable and X is a dependent feature vector (of size n) where:

Just to clarify, an example of a feature vector and corresponding class variable can be: (refer 1st row of the dataset)
X = (Rainy, Hot, High, False)
y = No
So basically, P(XU+007Cy) here means the probability of “Not playing golf,” given that the weather conditions are “Rainy outlook,” “Temperature is hot,” “high humidity,” and “no wind.”
Naive assumption
Now, its time to put a naive assumption to the Bayes’ theorem, which is independence among the features. So now, we split evidence into the independent parts.
Now, if any two events A and B are independent, then,
P(A,B) = P(A)P(B)
Hence, we reach the result:

which can be expressed as:
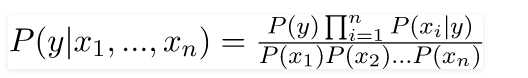
Now, as the denominator remains constant for a given input, we can remove that term:

Now, we need to create a classifier model. For this, we find the probability of a given set of inputs for all possible values of the class variable y and pick up the output with maximum probability. This can be expressed mathematically as:

So, finally, we are left with the task of calculating P(y) and P(xi U+007C y).
Please note that P(y) is also called class probability, and P(xi U+007C y) is called conditional probability.
The different naive Bayes classifiers differ mainly by the assumptions they make regarding the distribution of P(xi U+007C y).
Let us try to apply the above formula manually on our weather dataset. For this, we need to do some precomputations on our dataset.
We need to find P(xi U+007C yj) for each xi in X and yj in y. All these calculations have been demonstrated in the tables below:

So, in the figure above, we have calculated P(xi U+007C yj) for each xi in X and yj in y manually in the tables 1–4. For example, the probability of playing golf, given that the temperature is cool, i.e., P(temp. = cool U+007C play golf = Yes) = 3/9.
Also, we need to find class probabilities (P(y)), which has been calculated in table 5. For example, P(play golf = Yes) = 9/14.
So now, we are done with our pre-computations, and the classifier is ready!
Let us test it on a new set of features (let us call it today):
today = (Sunny, Hot, Normal, False)
So, probability of playing golf is given by:

and probability to not play golf is given by:
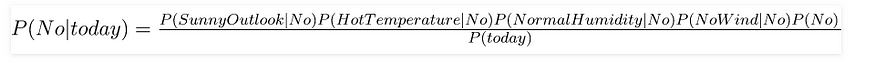
Since P(today) is common in both probabilities, we can ignore P(today) and find proportional probabilities as:

and

Now, since

These numbers can be converted into a probability by making the sum equal to 1 (normalization):

and
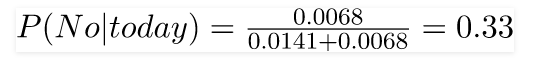
Since

So, the prediction that golf would be played is ‘Yes.’
The method that we discussed above is applicable to discrete data. In the case of continuous data, we need to make some assumptions regarding the distribution of values of each feature. The different naive Bayes classifiers differ mainly by the assumptions they make regarding the distribution of P(xi U+007C y).
Now, we discuss one of such classifiers here.
Gaussian Naive Bayes classifier
In Gaussian Naive Bayes, continuous values associated with each feature are assumed to be distributed according to a Gaussian distribution. A Gaussian distribution is also called Normal distribution. When plotted, it gives a bell-shaped curve which is symmetric about the mean of the feature values as shown below:
The likelihood of the features is assumed to be Gaussian; hence, conditional probability is given by:


Other popular Naive Bayes classifiers are:
- Multinomial Naive Bayes: Feature vectors represent the frequencies with which certain events have been generated by a multinomial distribution. This is the event model typically used for document classification.
- Bernoulli Naive Bayes: In the multivariate Bernoulli event model, features are independent booleans (binary variables) describing inputs. Like the multinomial model, this model is popular for document classification tasks, where binary term occurrence(i.e., a word occurs in a document or not) features are used rather than term frequencies(i.e., frequency of a word in the document).
As we reach the end of this article, here are some important points to ponder upon:
- Despite their over-simplified assumptions, naive Bayes classifiers have worked quite well in many real-world situations, famously document classification and spam filtering. They require a small amount of training data to estimate the necessary parameters.
- Naive Bayes learners and classifiers can be extremely fast compared to more sophisticated methods. The decoupling of the class conditional feature distributions means that each distribution can be independently estimated as a one-dimensional distribution, in turn, it helps to alleviate problems stemming from the curse of dimensionality.
References:
- https://en.wikipedia.org/wiki/Naive_Bayes_classifier
- http://gerardnico.com/wiki/data_mining/naive_bayes
- http://scikit-learn.org/stable/modules/naive_bayes.html
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














