
Correct Handling of Outliers to Improve Overfitting Scenarios
Last Updated on June 28, 2023 by Editorial Team
Author(s): Kayenga Campos
Originally published on Towards AI.
Correct Handling of Outliers to Improve Overfitting Scenarios
Look how quantile treatment of outliers can improve model accuracy
The main approach of machine learning consists of splitting the data into training and testing sets. Machine learning algorithms are then trained on the training set (dataset) to generalize from a pattern to unseen data, i.e., a test set. When an algorithm fails to generalize what it learned from the training set to the test set, it means the algorithm is overfitting.

Overfitting is a common problem in supervised learning, and in fact, two of the major tasks we face in classification are to identify it and overcome it. Endorsing it can compromise the quality of our model and even our reputation as data science experts.
If all the data in the test set follows the same distribution as the training set, why does overfitting occur?
The occurrence of overfitting is due to the possibility that the distribution of the training or test data may have irregularities that prevent the model from fitting to all the data. This is particularly likely in cases where learning takes place over a long period or when training examples are scarce, causing the model to adjust to specific random characteristics of the training set. These models generally violate Occam’s razor.

The faithful translation of these words is “Entities must not be multiplied beyond necessary”, based on these words, in an overfitting scenario, this can be interpreted as:
When there are two models with similar performance, always choose the simplest one.
For a practical example of the statistical approaches described in this post, let’s use iris data.
The dataset used in this article can be downloaded directly from the UCI repository, although it is also possible to call from the Scikit-learn library.
If you already have the dataset on your machine, you can load the data with pandas:
import pandas as pd
filename = "iris.csv"
names = ["SepalLength","SepalWidth","PetalLength","PetalWidth","Species"]
df = pd.read_csv(filename,names=names)
df.head(5)

The Iris plant dataset became popular thanks to the statistician and biologist R.A. Fisher when he presented it in his paper titled “The use of multiple measurements in taxonomic problems” as an example of linear discriminant analysis in 1936. It is now widely used in pattern recognition literature. This dataset has five variables, namely:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
— Iris Setosa
— Iris Versicolor
— Iris Virginica
As stated in the UCI repository, there are actually some irregularities in the iris data:
The 35th sample should be: 4.9,3.1,1.5,0.2,”Iris-setosa” where the error is in the fourth feature. Sample 38th: 4.9,3.6,1.4,0.1,”Iris-setosa” where the errors are in the second and third features.
Can this affect the performance of our model? It can, even though the difference may seem insignificant given the considerable number of correctly collected data. However, we should always choose to correct any irregularities found in our training set.
We proceed to obtain a statistical description of our data and also call a pandas function to count the number of our output class (Species): We have 3 classes with 50 members each.
We can also check the mean, standard deviation, and quantiles of each class:
df.describe()
class_count = df.groupby('Species').size()
class_count

We have 3 classes of 50 members each, we can also check the mean, standard deviation, and quantiles of each class.
We can have a visual description of our data.
import matplotlib.pyplot as plt
# Set species and colors
species = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['blue', 'orange', 'red']
plt.figure(figsize=(8, 6))
for i, sp in enumerate(species):
subset = df[df['Species'] == sp]
plt.scatter(subset['SepalLength'], subset['SepalWidth'], color=colors[i], label=sp)
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('Scatter Plot of Iris Species')
plt.show()

In fact, based on the size of the sepal and the petal, it is possible to establish the following rules:
If petal-length < 2.45 then Iris-setosa
If sepal-width < 2.10 then Iris-versicolor
If sepal-width < 2.45 and petal-length < 4.55 then Iris-versicolor
If sepal-width < 2.95 and petal-width < 1.35 then Iris-versicolor
If petal-length < 2.45 and petal-length < 4.45 then Iris-versicolor
If sepal-length >= 5.85 and petal-length < 4.75 then Iris-versicolor
If sepal-width < 2.55 and petal-length < 4.95 and petal-width < 1.55 then
iris versicolor
If petal-length >= 2.45 and petal-length < 4.95 and petal-width < 1.55 then
iris versicolor
If sepal-length >= 6.55 and petal-length < 5.05 then Iris-versicolor
If sepal-width < 2.75 and petal-width < 1.65 and sepal-length < 6.05
then iris-versicolor
If sepal-length >= 5.85 and sepal-length < 5.95 and petal-length < 4.85
then iris-versicolor
If petal-length >= 5.15 then Iris-virginica
If petal-width >= 1.85 then Iris-virginica
If petal-width >= 1.75 and sepal-width < 3.05 then Iris-virginica
If petal-length >= 4.95 and petal-width < 1.55 then Iris-virginicaIf petal-length >= 5.15 then Iris-virginica
If petal-width >= 1.85 then Iris-virginica
If petal-width >= 1.75 and sepal-width < 3.05 then Iris-virginica
If petal-length >= 4.95 and petal-width < 1.55 then Iris-virginica
The next step is to standardize our data, some algorithms perform better when exposed to a normal distribution, we can try to achieve this through the Z-Score transformation.

Where x is the number of elements in the dataset.
Take care using this formula. When the data is multidimensional, you must modify this formula to:

But before going to the next step, let’s review some concepts about Gaussian distribution and the z-score itself.
In a Gaussian distribution also called normal distribution, about 68.3% of the records are between:

About 95.4% of the records are between:

About 99.7% of the records are between:

In summary:

In fact, according to the central limit theorem, it is only possible to reach a standard normal distribution with the Z-Score transformation when the number of samples is large enough; when the number of samples is not large enough, we will encounter a T-Student distribution. The T-Student distribution is similar to a normal distribution, with a flatter bell shape depending on the degrees of freedom; in general, the greater the degrees of freedom, the closer it is to a normal distribution.

It is often said that after the Z-Score transformation we have a mean of 0 and a standard deviation of 1, but in fact the Z-Score itself is a random variable, the value of the variance is not known for sure, just an estimate that is approximations to these values.
An Overfitting Arises
We will evaluate a common overfitting scenario; we will train a logistic regression model to classify our Iris data. To simulate an overfitting scenario, we will divide the data into training (90%) and test sets (10) without randomizing the data; as the data is ordered, this will allow us to capture all records of the iris setosa and iris versicolor classes and only 70% of the iris virginica classe, as the algorithm trained on only a few data from this class it will not perform well when evaluating data not seen in this class, In other words, it is possible to deduce that we have to overfit. Our goal is to create an approach to improve the model’s performance up to 100% without randomizing the data or exposing the model to more training data. Is this possible? We will see next.
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
array = df.values
X = array[:,0:4] # data
Y = array[:,4] # label
# Standardize the data
X = (X - np.mean(X))/2*np.std(X)
# Reserve 10% to test.
split = int(X.shape[0]*0.9)
X_train = X[0:split]
Y_train = Y[0:split]
X_test = X[split:]
Y_test = Y[split:]
model = LogisticRegression(max_iter=1000)
model.fit(X_train, Y_train)
result = model.score(X_test, Y_test)
Our model is accurate to 93%. This looks fantastic, but there is actually a problem to solve, our model was not able to correctly classify the records of the virginica class as expected, and as we set out to solve it, we must look for a way to improve the performance of our model for that class.
The approach to solve this problem is in the statistical treatment for outliers. Outliers are values outside the distribution of our data, the type of graph that best describes them is boxplots, here is a small description of how to interpret them.
df.plot(kind='box')

As it is in the image, these dots outside the whiskers are our outliers. We observe that SepalWidth have outliers, fortunately, we have a way to locate them, so let’s analyze our problem more statistically:
Being X a variable of the setosa, virginica or versicolor class, X is an outlier if:

Or alternatively:
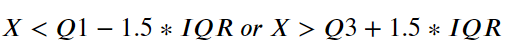
Now we know how to hunt for an outlier, we just need to translate this into our favorite programming language. Ah! We need to replace the outlier points with standard deviation.
def outlier_search(column):
quantile1 = df[column].quantile(0.25)
quantile3 = df[column].quantile(0.75)
inter_quantile = quantile3 - quantile1
out_found = df.loc[(df[column] < (quantile1 - (1.5*inter_quantile))) U+007C (df[column] > (quantile3 + (1.5*inter_quantile))), column] = df[column].std()
return column
outlier_search('SepalWidth')
Let’s visualize the boxplots again.

We seem to have achieved a very significant improvement in our data.
Unfortunately, there is no clear pattern for handling outliers, so we need to make some adjustments to the formula to improve the model’s score. Let’s modify the quantile3 variable by dividing it by 2. Our final formula should look like this:

Now that we’ve gathered all the variables, all that’s left is to put it all together and see what result we can get from it:
...
...
def outlier_search(column):
quantile1 = df[column].quantile(0.25)
quantile3_optimized = (df[column].quantile(0.75))/2
inter_quantile = df[column].quantile(0.75) - df[column].quantile(0.25)
out_found = df.loc[(df[column] < (quantile1 - (1.5*inter_quantile))) U+007C (df[column] > (quantile3_optimized + (1.5*inter_quantile))), column] = df[column].std()
return column
outlier_search('SepalWidth')
array = df.values
X = array[:,0:4] # data
Y = array[:,4] # test
# Standardize the data
X = (X - np.mean(X))/2*np.std(X)
# Reserve 10% to test
split = int(X.shape[0]*0.9)
X_train = X[0:split]
Y_train = Y[0:split]
X_test = X[split:]
Y_test = Y[split:]
model = LogisticRegression(max_iter=1000)
model.fit(X_train, Y_train)
result = model.score(X_test, Y_test)
Wow! Our model score is now 100%! We achieve our goal simply by offering an approach to dealing with outliers.
Conclusion
In this article, we try to discuss the problem of overfitting and how it affects our model, we found that deleting the outliers could significantly improve our model, and in the end, we present a statistical way of how to locate the outliers in our data.
We also made a comparison of accuracy with and without outliers, this is just one approach to deal with the overfitting problem that caters to a scenario where the training data is unbalanced.
Disclaimer: The main purpose of this article is to prove that handling outliers can really significantly improve the train data score, so the overfitting scenario was created intentionally; you should use some approach to avoid overfitting, like cross-validation.
I hope this post has clarified what it is, and how to deal with this problem.
Thanks for reading the post!
Follow me for more content like this one, it helps a lot!
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














