K-Means Simplified
Last Updated on October 28, 2020 by Editorial Team
Author(s): Luthfi Ramadhan
Data Science, Machine Learning
Short Introduction and Numerical Example of K-Means Clustering

What is clustering?
Clustering is the process of grouping a set of data objects (or observations) into subsets. Each subset is a cluster, such that objects in a cluster are similar to one another but different from objects in other clusters. Clustering is commonly used to explore a dataset to either identify the underlying patterns in it or to create a group of characteristics.
Clustering is sometimes called automatic classification. Because a cluster is a bunch of data that are similar to one another within the same cluster and dissimilar to data in other clusters so that a cluster of data can be treated as an implicit class. The difference here is that clustering can automatically find the groupings. This is a distinct advantage of clustering.
Clustering has been widely used in many applications one of which is business intelligence. In business intelligence, clustering can be used to organize a large number of customers into groups, where customers within a group share strong similar characteristics. By doing this, it is easier to develop business strategies for enhanced customer relationship management.
In this context, different clustering methods may generate different clusterings on the same data set. The grouping is not performed by humans, but by the clustering algorithm such as K-means. Hence, clustering is useful in that it can lead to the discovery of previously unknown groups within the data.
What is K-means?
K-means is a well-known algorithm used to perform clustering. The idea of k-means is that we assume there are k groups in our dataset. We then try to group the data into those k groups. Each group is described by a single point known as a centroid. The centroid of a cluster is the mean value of the points within the cluster.
How K-means actually work?
First, it randomly creates k centroids where k is the number of the cluster we are aiming to. Each sample is assigned to the cluster to which it is the most similar based on the euclidean distance between sample and cluster centroid. Then it updates each centroid using the mean of the assigned sample. All the samples are then reassigned using the updated centroids. The iterations continue until the assignment is stable or there is no difference between the new assignment and the previous iteration assignment. The k-means procedure is summarized as follows:
- Choose the number of k clusters.
- Initialize k number of centroids.
- Assign each sample to the closest centroid based on its euclidean distance.
- Update the new centroid of each cluster using the mean of the assigned sample.
- Reassign each sample to the new centroid. If any reassignment took place, repeat step 4 otherwise stop the iteration.
Example
Here is a dummy dataset containing 10 samples:
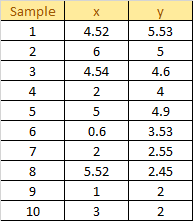
Plot the dataset using Scatter plot:
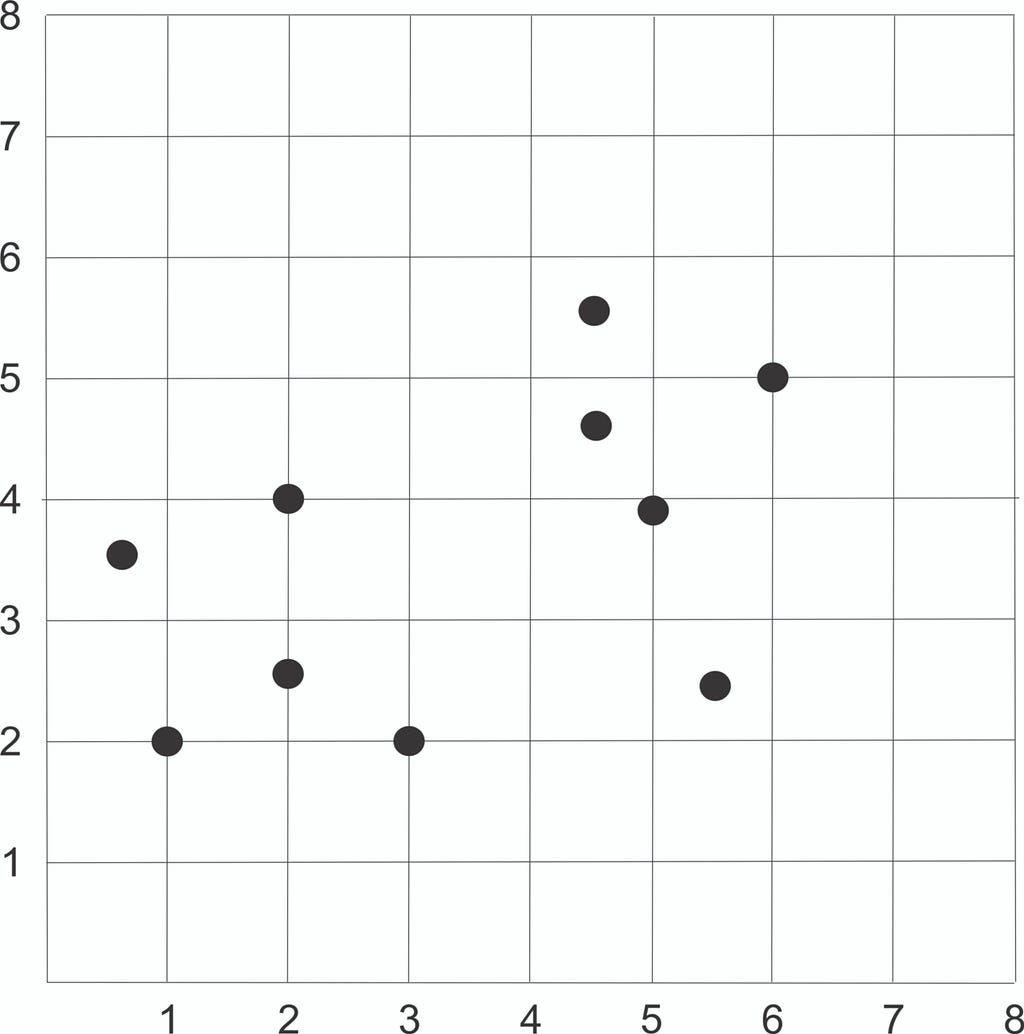
Step 1: Choose the number of K Clusters
let say we want to cluster the data into 2 clusters.
Step 2: Initialize Centroid
Initialize 2 random centroids:
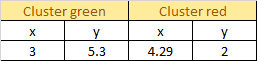
Plot the dataset using Scatter plot:
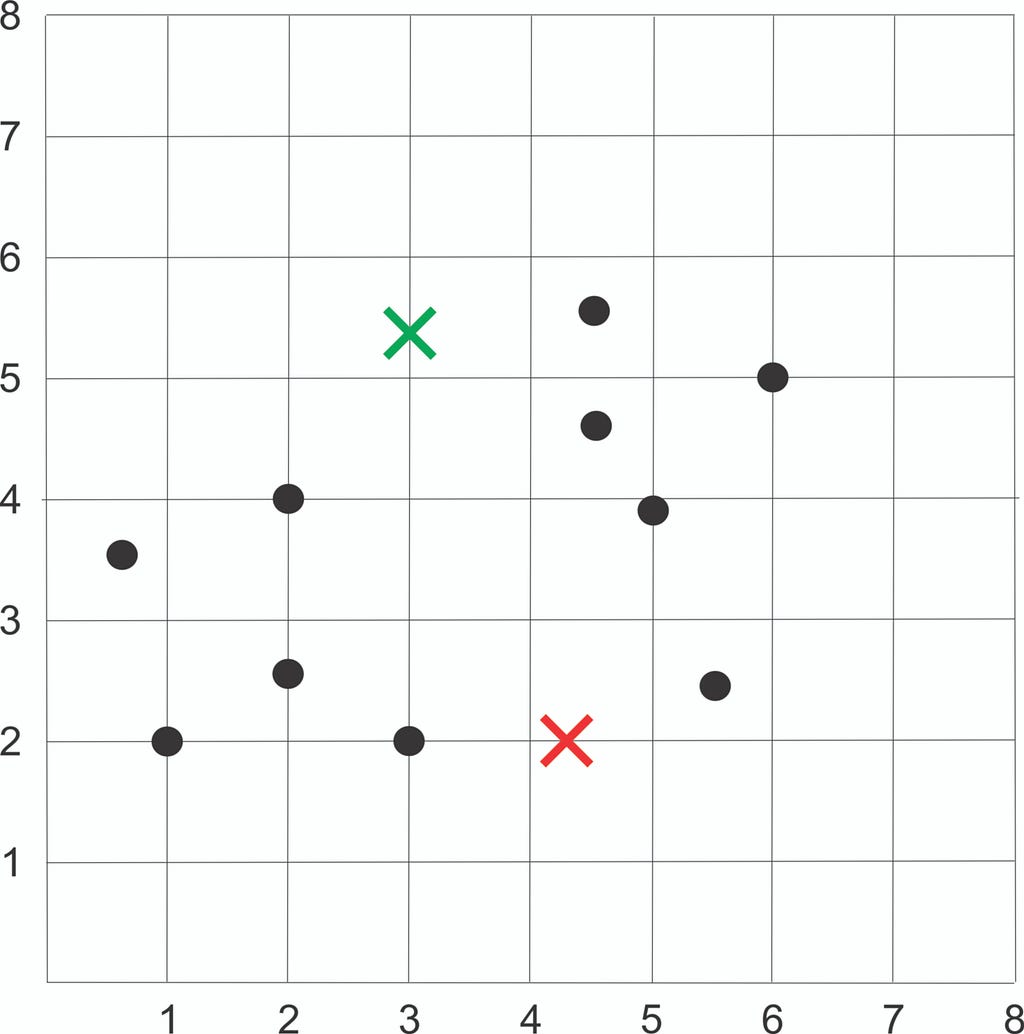
Step 3: Assign each sample to the closest centroid
We then compute Euclidean distance between each sample and each centroid with the following formula:
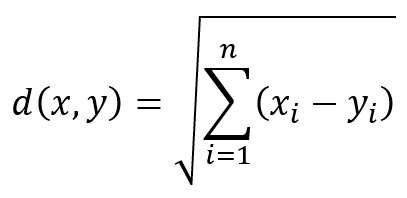
Current Centroid:
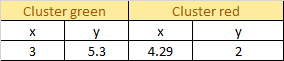
Apply the formula into our data, we get the result as follow:
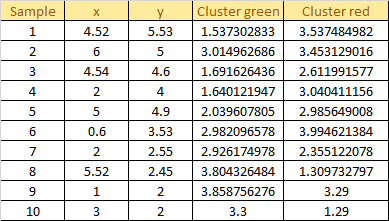
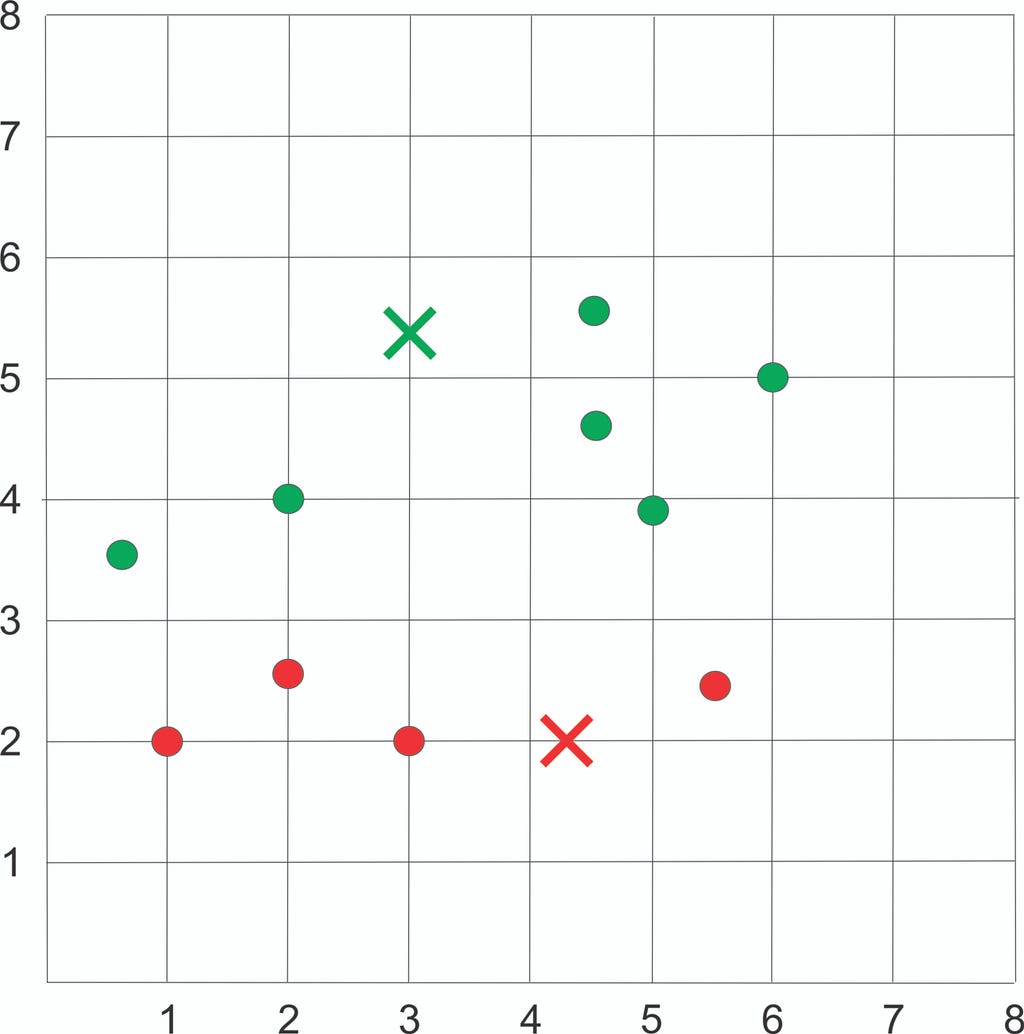
Assign each sample to the closest centroid based on previously obtained euclidean distance.
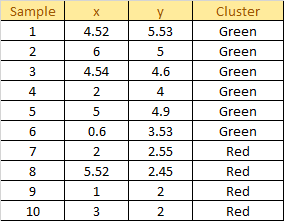
Plot the dataset using Scatter plot:
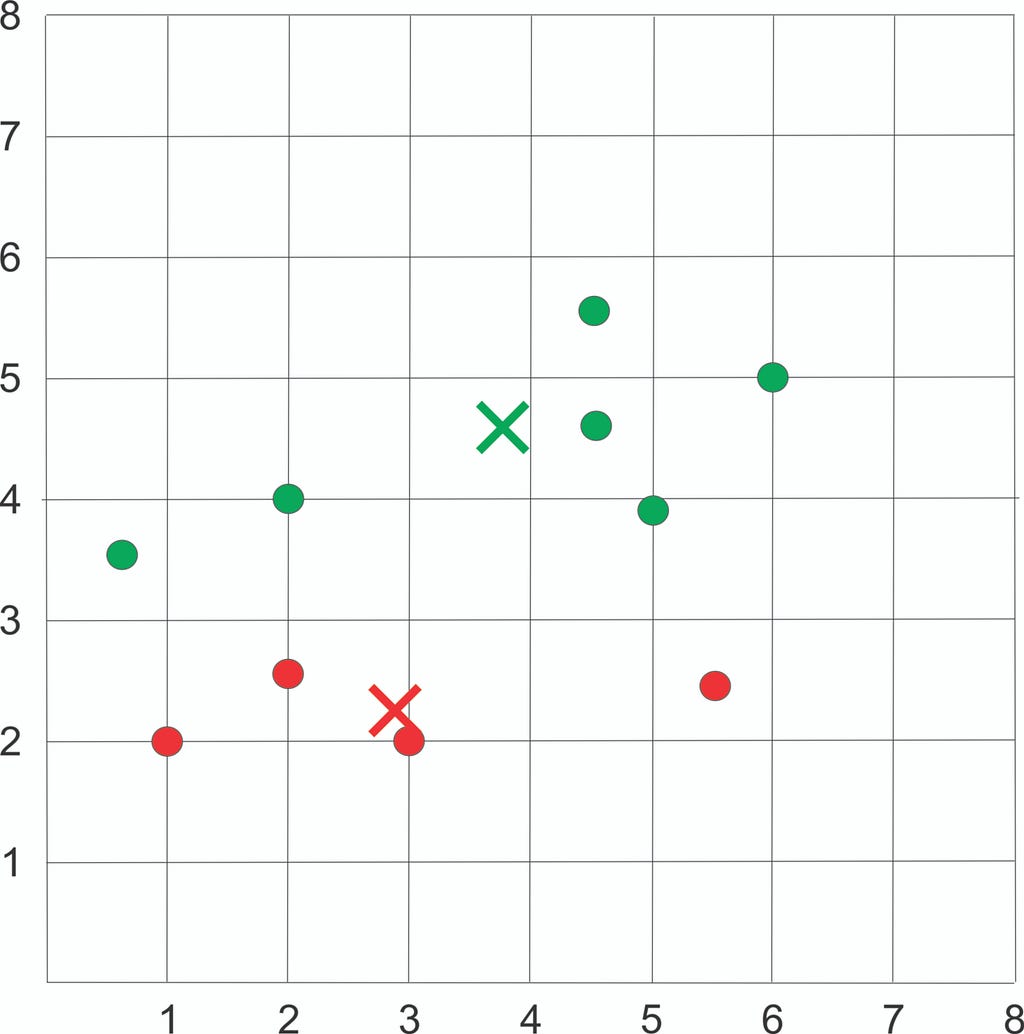
Step 4: Update the new centroid
We then update the centroid using the mean of the assigned sample in each cluster.
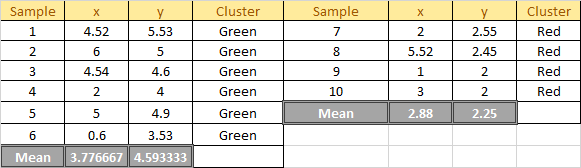
Plot the dataset using Scatter plot:
Step 5: Reassign each sample to the new centroid. If any reassignment took place, back to step 4 otherwise stop the iteration.
Compute Euclidean distance between each sample and each new centroid.
Current Centroid:
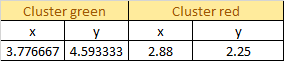
Distance Between each sample and each centroid:
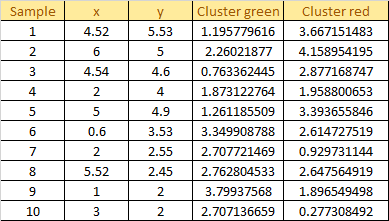
Assign each sample to the closest centroid based on previously obtained euclidean distance:
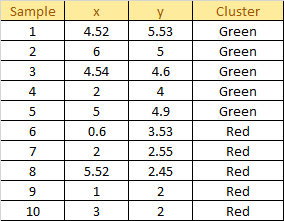
Plot the dataset using Scatter plot:
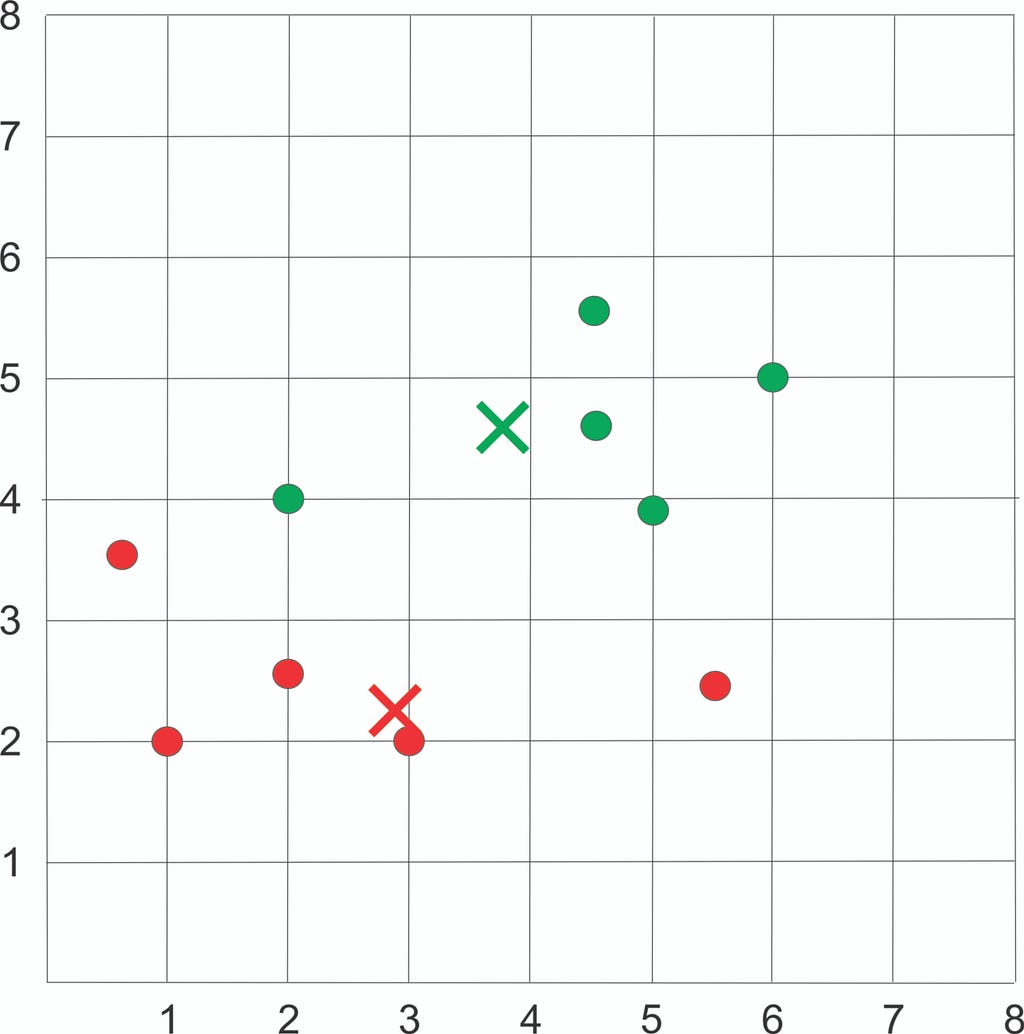
Check for reassignment:
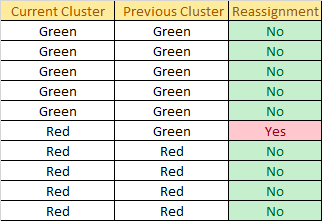
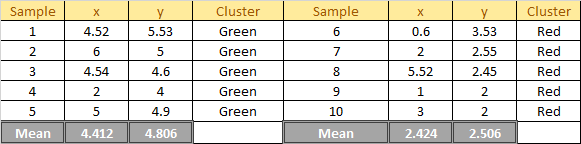
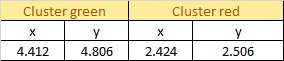
1 Reassignment happens, so we back to step 4. Update the centroid using the mean of the assigned sample in each cluster:
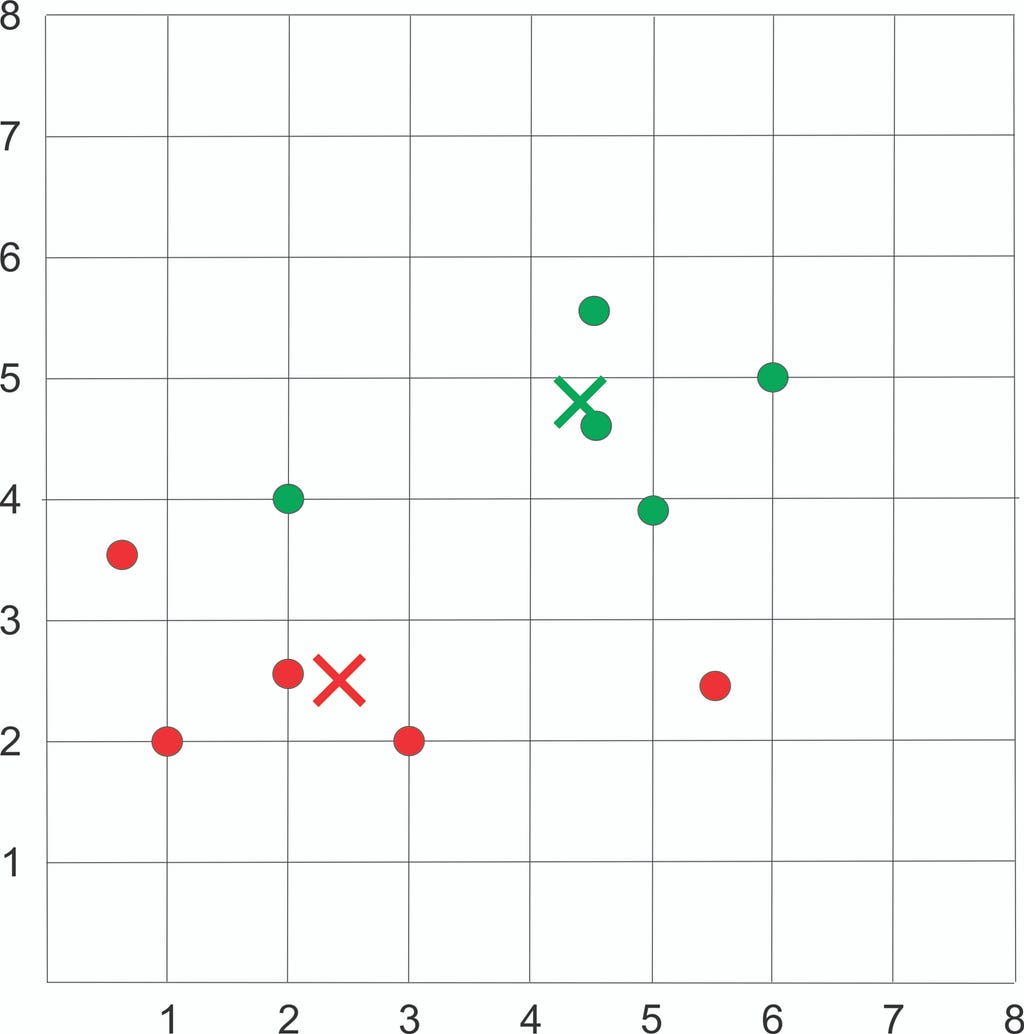
Plot the dataset using Scatter plot:
Compute Euclidean distance between each sample and each new centroid.
Current Centroid:
Distance Between each sample and each centroid:
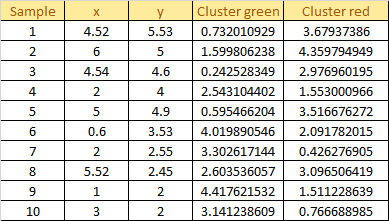
Assign each sample to the closest centroid based on previously obtained euclidean distance:
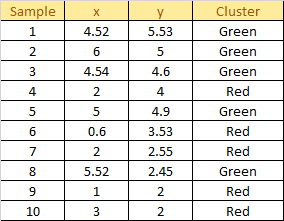
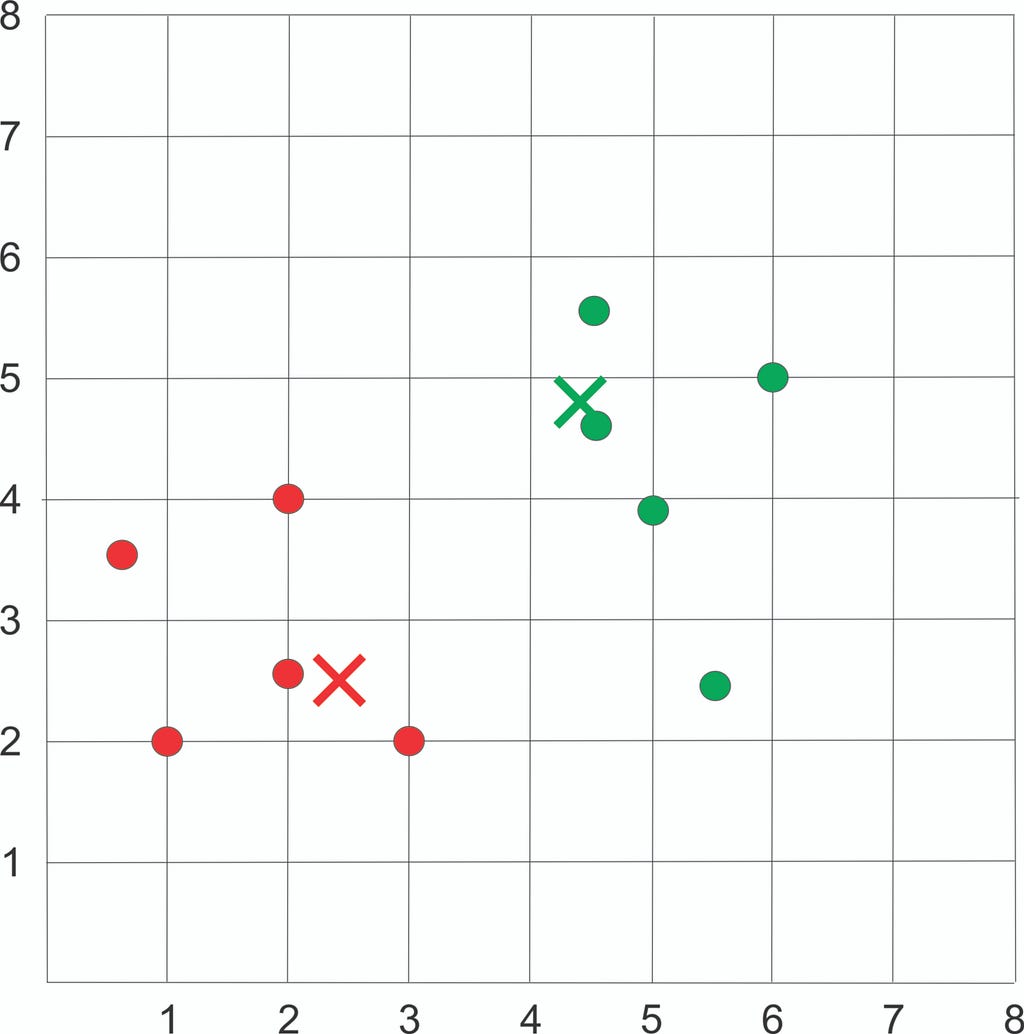
Plot the dataset using Scatter plot:
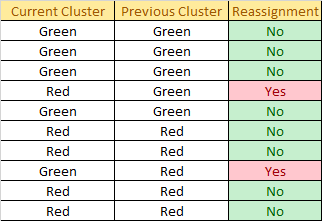
Check for reassignment:
2 Reassignments happen, so we back to step 4. Update the centroid using the mean of the assigned sample in each cluster:
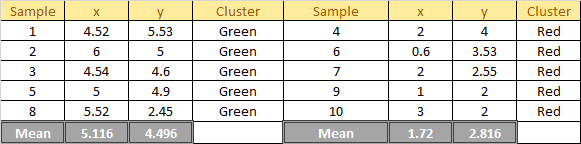
Plot the dataset using Scatter plot:
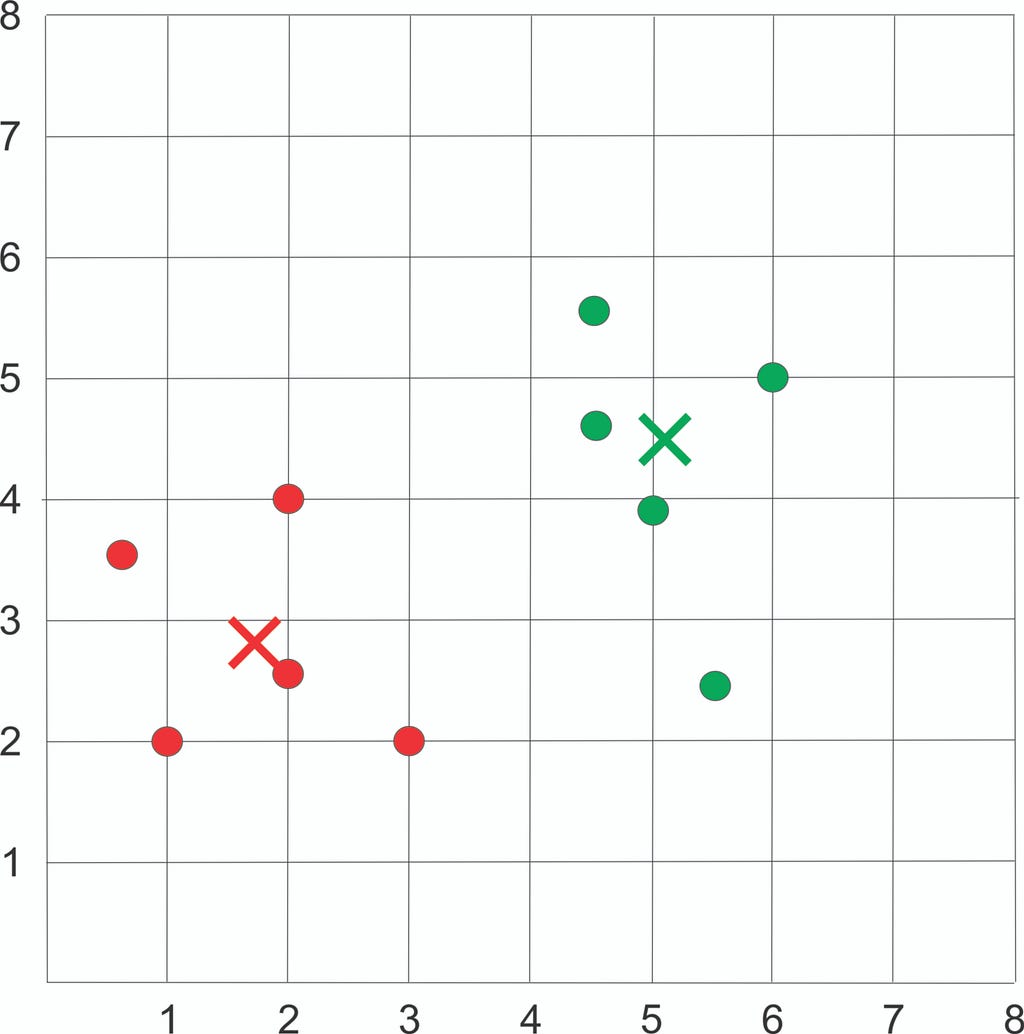
Compute Euclidean distance between each sample and each new centroid.
Current Centroid:
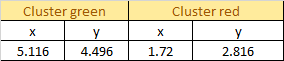
Distance Between each sample and each centroid:
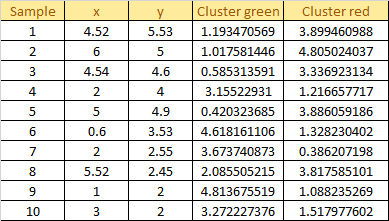
Assign each sample to the closest centroid based on previously obtained euclidean distance:

Plot the dataset using Scatter plot:
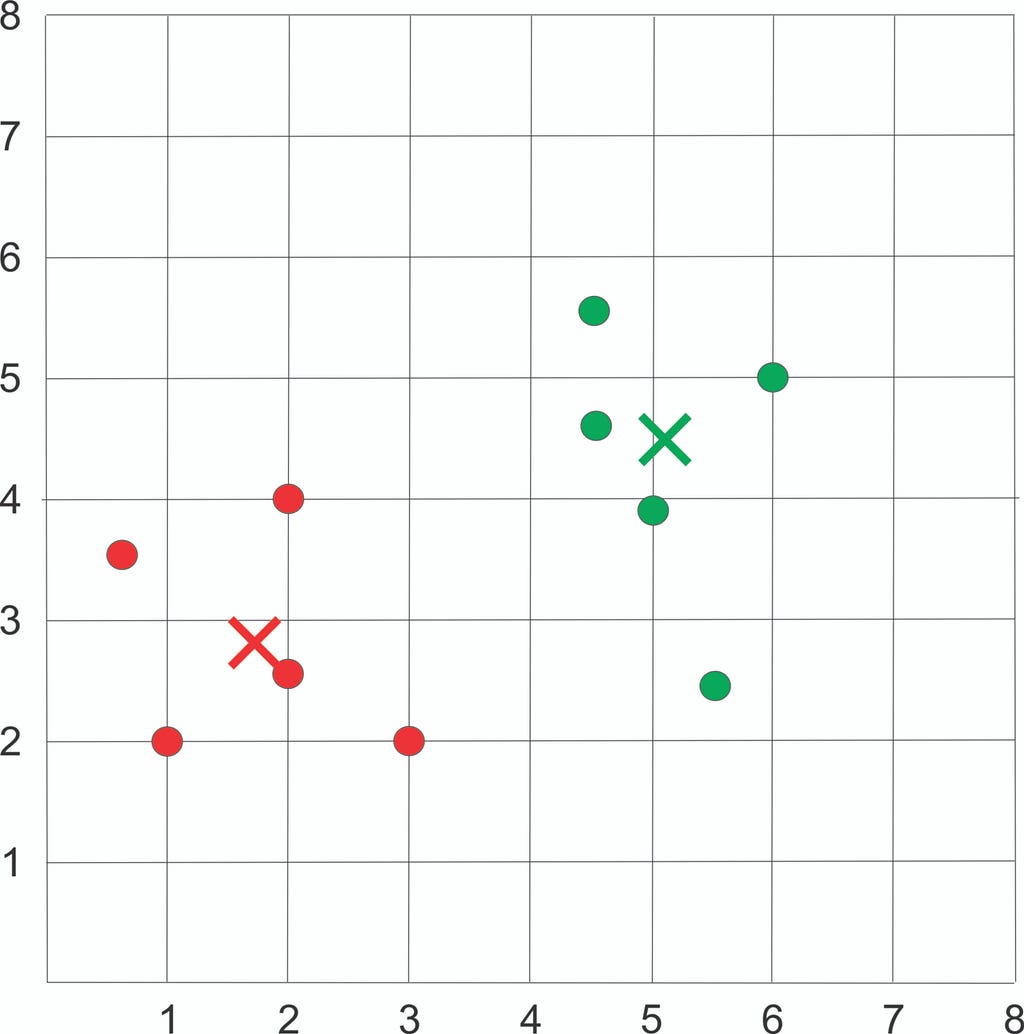
Check for reassignment:
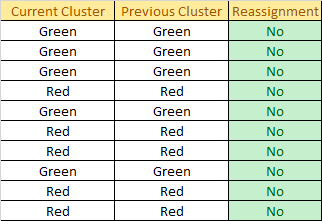
No assignment happens, so we stop the iteration and get the final result as follow:

Plot the dataset using Scatter plot:

K-Means Disadvantage
The k-means algorithm is not guaranteed to converge to the global optimum and often terminates at a local optimum. The results will highly depend on the initial centroid. To get better results, it is common to run the k-means algorithm several times with different initial centroid and a different number of k clusters.
References
[1] J. Han, M. Kamber, and J. Pei, Data Mining Concepts and Techniques (2011)
[2] Sung-Soo Kim, What is Cluster Analysis? (2015)
K-Means Simplified was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














