Word Mover’s Distance (WMD) Explained: An Effective Method of Document Classification

Last Updated on September 22, 2020 by Editorial Team

Author(s): Xiao Tan

Natural Language Processing

[Reading] From Word Embeddings To Document Distances

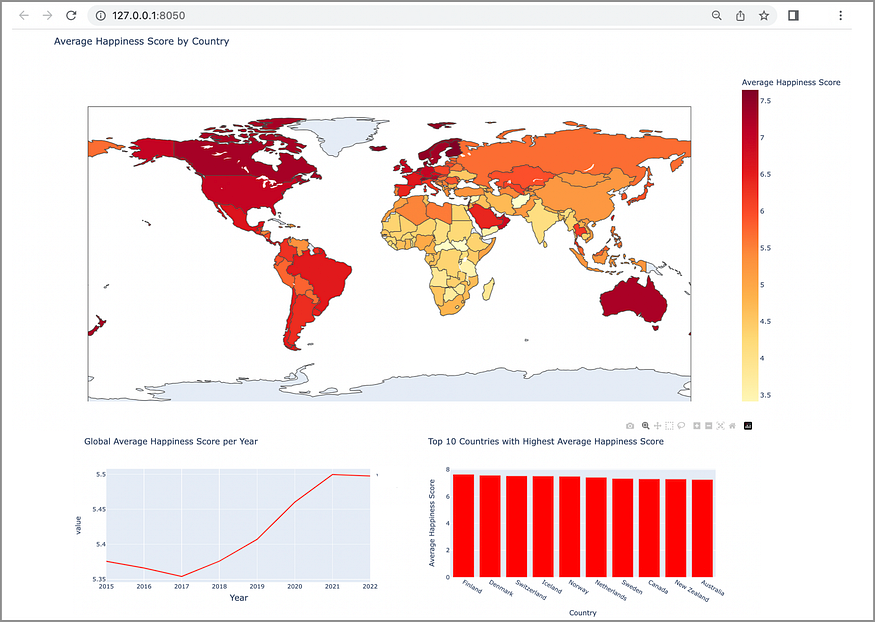
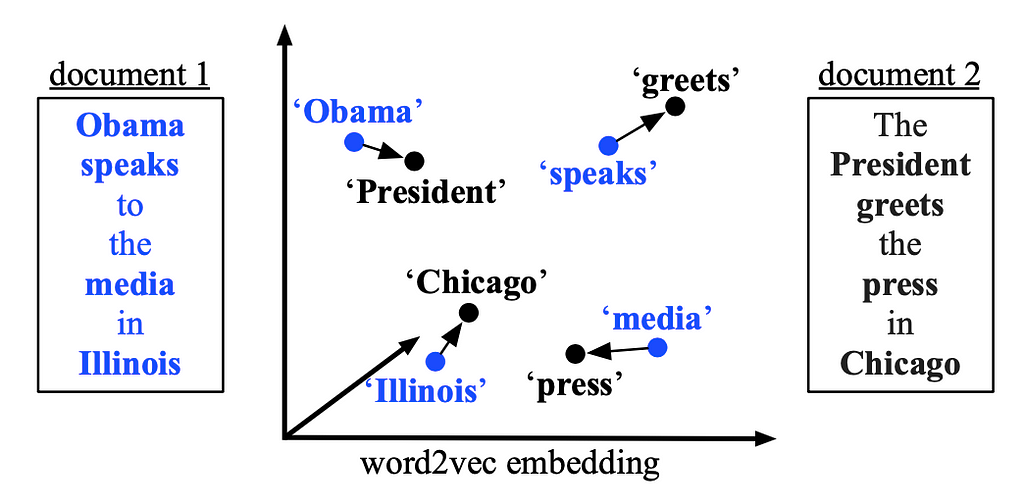
Document classification and document retrieval have been showing a wide range of applications. An essential part of document classification is to generate document representations properly. Matt J. Kusner et al., in 2015, presented Word Mover’s Distance (WMD) [1], where word embeddings are incorporated in computing the distance between two documents. With given pre-trained word embeddings, the dissimilarities between documents can be measured with semantical meanings by computing “the minimum amount of distance that the embedded words of one document need to ‘travel’ to reach the embedded words of another”.

In the following sections, we will be discussing the principle of WMD, the constraints and approximations, prefetch and prune of WMD, the performance of WMD.

Principle of WMD

As aforementioned, WMD tries to measure the semantic distance of two documents, and the semantic measurement is brought by word2vec embeddings. Specifically, skip-gram word2vec is utilized in their experiments. Once the word embeddings are obtained, the semantic distance among documents is defined by the following three parts: document representation, similarity metric, and a (sparse)flow matrix.

Text document representation

A text document is represented as a vector d, in which each element denotes a word’s normalized frequency in the document, i.e.

Note that the document representation d is a sparse vector in high dimensional space.

Semantic similarity metric definition

The Euclidean distance in embedding space of two given words, x_i and x_j, is defined as follows:

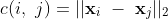
In WMD, x_i and x_j are from different documents, and c(i, j) is the “travel cost” from word x_i to x_j.

Flow matrix definition

Suppose there are a source document A and a target document B. A flow matrix T is defined. Each element in the flow matrix, T _{ij}, denotes how many times of word i (in document A) transforms into word j (in document B), then normalize the value by the total count of words in the vocabulary. That is to say,

Therefore, the semantic distance definition is as follows:

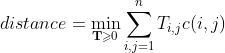
By tuning values in T, the semantic distance between two documents can be obtained. The distance also is the minimum cumulative cost required to move all words from one document to the other.

Constraints and lower-bound approximations

There are two constraints on the minimum cumulative cost, which is

Overall, the computational complexity of constrained minimum cumulative cost is O(p³logp), where p is the number of unique words in the documents. That is to say, WMD may not be applicable on large documents, or documents with large number of unique words. In the paper, the authors proposed two ways to speed up WMD computation. Both speed-up methods lead to approximations of the actual WMD value.

Word centroid distance (WCD)

By using triangle inequality, the cumulative cost can be proven to be always greater than or equal to the Euclidian distance between document vectors weighted by the average of word embeddings. In this way, the computational complexity is dropped to O(dp) (here, d represents the dimension of the document vector d.)

Relaxed WMD (RWMD)

There are two constraints in the objective. If removing one constraint, the optimal solution for the cumulative cost is for each word in one document to move all its probability mass to the most similar word in the other document. This means the cost minimization problem is turned into finding the minimum Euclidian distance of two-word embeddings in the embedding space. Therefore, by removing one constraint and keeping the other, there are two approximated lower bounds: let’s call them l1(keep the constraint on i) and l2 (keep the constraint on j). A tighter approximation l can be defined as:

l=max(l1, l2).

With this approximated cumulative cost, which the authors refer to as Relaxed WMD (RWMD), the computational complexity is dropped to O(p²).

Prefetch and prune

In order to find the k nearest neighbors of a query document with efficient time, WCD and RWMD can both be utilized to reduce the computational cost.

1. Use WCD to estimate the distance between each document to the query document.
2. Sort the estimated distances by ascending order, then compute the exact distance using WMD to the first k of these documents.
3. Traverse the remaining documents (which are not among the first k from the previous step), computing the RWMD lower bounds.
4. If the RWMD approximation of a document (to the query document) is greater than all the computed WMD distances to the first k documents (in step 2), that means this document must not be in the k nearest neighbors of the query document, thus it can be pruned. Otherwise, the exact WMD distance is computed and update to the k nearest neighbors.

Performance of WMD

The authors evaluated the WMD performance in the context of kNN on eight document datasets and compared the performance with BOW, TFIDF, BM25 LSI, LDA, mSDA, CCG. Their experiments show that WMD performs the best on 6 out of 8 datasets. For the rest 2 datasets, even though WMD is not with the best performance, the error rates are very close to the best performers.

An interesting experiment result is the author performed an experiment of evaluating the relationship between the tightness of the lower bounds and the kNN error rates if the lower bounds are used for nearest neighbor retrieval. It shows that the tightness does not directly translate into retrieval accuracy. In the authors’ statement, the tightness of RWMDs in which only takes one constraint at a time, named as RWMD_c1 and RWMD_c2, is significantly higher than WCD, yet both RWMD_c1 and RWMD_c2 perform worse than WCD regarding kNN accuracy. To my point of new, this could due to the asymmetric constraints casted on RWMD_c1 and RWMD_c2. Because only remaining one constraint derives to the non-strict definition of a distance metric, and neither RWMD_c1 nor RWMD_c2 is strict distance approximations.

Potential expansion of work

WMD’s performance has shined in the document classification tasks. In my opinion, there are several things that can be experimented for further exploration regarding WMD.

The authors have utilized different datasets for word embedding generation, but the embedding method has stuck to word2vec with skip-gram. It would be interesting to see the significance of the embedding methods to WMD by changing word2vet to other methods, such as GloVe.

Note that WMD cannot handle out of vocabulary (OOV) data, and it directly throws the OOV words away when encountered in distance computation. This could be a reason that the WMD performance does not outweigh all other methods across all datasets. OOV words’ embeddings can be built based on contextual information. For instance, a BiLSTM language model could help on generating OOV word embeddings [2]. Also, Byte Pair Encoding (BPE) may build OOV word embeddings as well.

References

[1] Original paper: From Word Embeddings To Document Distances

[2] https://www.researchgate.net/publication/335757797_Language_Modelling_for_Handling_Out-of-Vocabulary_Words_in_Natural_Language_Processing?showFulltext=1&linkId=5d7a26a04585151ee4afb0c5

[3] WMD code

Word Mover’s Distance (WMD) Explained: An Effective Method of Document Classification was originally published in Towards AI — Multidisciplinary Science Journal on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI