Part 03: Describing Random Outcomes: PMF, CDF, and PDF

Author(s): Sudeep

Originally published on Towards AI.

In the previous article, we introduced the concept of a random experiment using the example of student marks in a class. Now, we will delve deeper into how we mathematically describe the likelihood of different outcomes using key functions from probability theory

To understand the results of a random experiment like observing student marks, we need ways to quantify the probabilities of different outcomes. This involves defining a random variable (like the score itself) and describing its probability distribution.

Let’s assume the “test score” (our random variable, let’s call it X) can only take discrete integer values from 1 to 100.

Probability Mass Function (PMF)

For a discrete random variable, the PMF gives the probability that the variable takes on exactly a specific value.

In simple terms: It answers, “What is the probability that the score X is exactly equal to x?” We write this as P(X = x).

Imagine a class of 10 students who took a mock test, and their scores (out of 100) are:
55, 70, 85, 60, 75, 90, 80, 95, 70, 65

Step 1: Frequency Calculation
Let’s calculate the frequency of each score:

• 55: 1 occurrence
• 60: 1 occurrence
• 65: 1 occurrence
• 70: 2 occurrences
• 75: 1 occurrence
• 80: 1 occurrence
• 85: 1 occurrence
• 90: 1 occurrence
• 95: 1 occurrence

Step 2: Calculate PMF
The PMF gives the probability of each mark occurring:

For example,

The PMF tells us the likelihood of students scoring exactly a specific mark. For instance, the probability of scoring 70 is 0.2 or 20%.

Cumulative Distribution Function (CDF)

The CDF gives the probability that a random variable (discrete or continuous) takes on a value less than or equal to a specific value x. It represents accumulated probability.

In simple terms: It answers, “What is the probability that the score X is at most x ?” We write this as F(x) = P(X ≤ x).

Example (Discrete Marks)

• Step 1: Cumulative Sum Calculation.

For example,

This means there’s a 50% chance a randomly chosen student scored 70 or less.

What if the Variable is Continuous? The Probability Density Function (PDF)

• Sometimes, variables can take any value within a range (e.g., height, exact time, or if marks could be 75. K5, 81.2, etc.). These are continuous random variables.
• For continuous variables, we use the Probability Density Function (PDF), denoted f(x). To find the probability over an interval, we calculate the area under the curve:

• Key Difference: The PDF f(x) itself does not give the probability that X equals x (that probability is actually 0 for continuous variables). Instead, the PDF describes the relative likelihood or density of the variable around the value x.
• CDF for Continuous: The CDF F(x) = P(X ≤ x) still works similarly, but it’s calculated by integrating the PDF from the minimum possible value up to x.

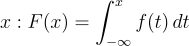
Real-World Applications

Education Analytics:

• PMF: Analyzing the frequency of specific scores to understand grade distributions.
• CDF: Determining the proportion of students scoring below a certain threshold.

Risk Assessment:

• Using PDFs and CDFs to evaluate the likelihood of certain financial events or insurance claims.

Quality Control:

• Estimating defect rates in manufacturing by modeling the probability of various outcomes.

Summary: Understanding Random Experiments

• Probability Mass Function (PMF): Describes the likelihood of discrete outcomes, answering “What is the probability that X equals x?”
• Cumulative Distribution Function (CDF): Accumulates probabilities up to a certain value, providing the chance that X is less than or equal to x.
• Probability Density Function (PDF): For continuous variables, describes the density of outcomes, where probabilities are calculated as areas under the curve.

Next stop: Estimation of Population and Hypothesis Testing.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI