Types of Activation Function

Author(s): Saurabh Saxena

Originally published on Towards AI.

Activation Function in Neural Networks

An Activation Function decides whether a neuron should be activated or not, sometimes, it is also called a transfer function. The primary role of the activation function is to transform the summed weighted input from the previous layers into an output fed to the neurons of the next layer.

Let’s look at the architecture of the neuron in the Neural Network.

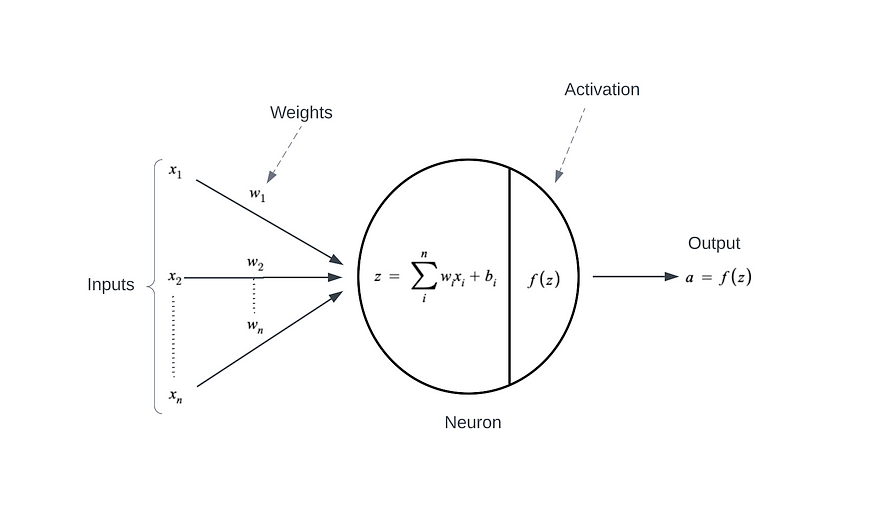
The main purpose of the Activation Function is to add non-linearity to the linear model. It introduces an additional step at each layer during forwarding propagation. If we don’t place the Activation function, each neuron will act as a linear function which, in turn, the entire network into the linear regression model.

Let’s go over the popular activation function used in neural networks.

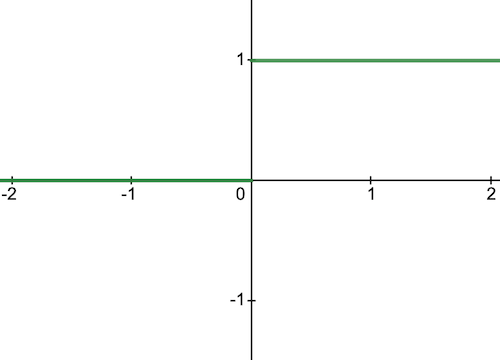
1) Binary Step Activation Function

Neurons should be activated or not in a layer depending on a specific threshold value.

The input fed to the activation function is compared to a threshold. If the input is greater than it, then the neuron is activated, or else it is deactivated.

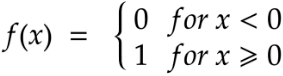
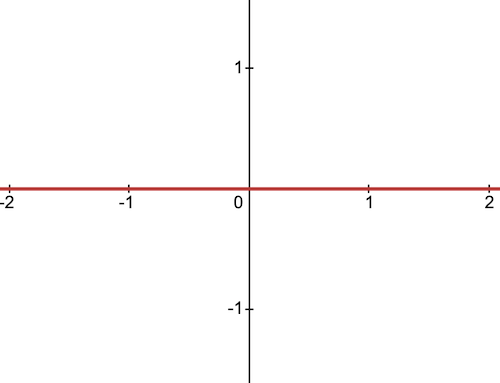
Below is the derivative of the binary step function

Below are some of the limitations of a binary step function:

• It cannot be used for multi-class classification problems.
• The gradient of the function is zero, which causes a hindrance in the backpropagation process.

2) Linear Activation Function

The linear activation function, also known as no activation or identity function, is where the activation is proportional to the input. The function simply spits out the value it was given.

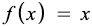
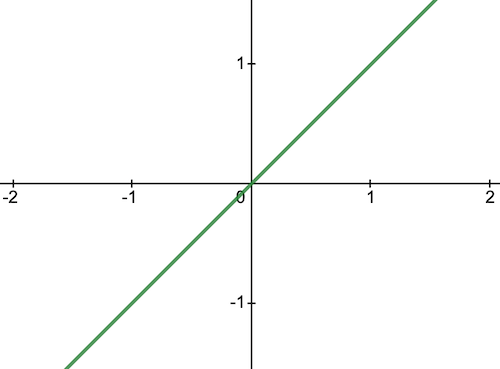
Below is the first derivative of a linear function

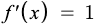
Here are a few limitations of a linear function:

• It’s not possible to use backpropagation as the derivative of the function is a constant and has no relation to the input.
• No matter the number of layers in the neural network, the last layer will still be a linear function of the first layer. So, a linear activation function turns the neural network into just a one-layer network.

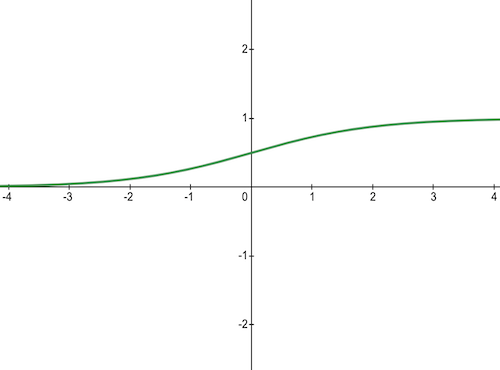
3) Sigmoid Activation Function

This function takes any real value as input and outputs values in the range of 0 to 1. The larger the input (more positive), the closer the output value will be to 1, whereas the smaller the input (more negative), the closer the output will be to 0.

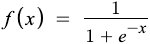
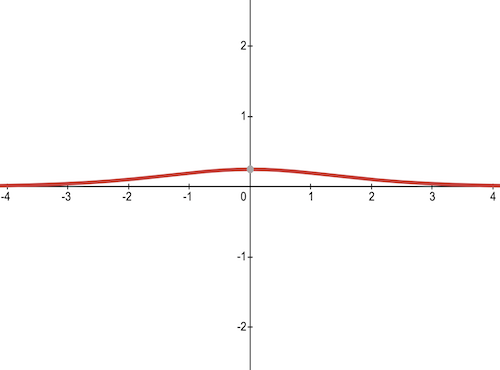
Here is the derivative of a sigmoid function

• It is commonly used for models where we have to predict the probability as an output.
• The function is differentiable and provides a smooth gradient.

Here are a few limitations of the sigmoid function:

• The gradient values are only significant for the range -3 to 3, and the graph gets much flatter in other regions.
• For values greater than 3 or less than -3, the function will have very small gradients. As the gradient value approaches zero, the network suffers from the Vanishing gradient problem.
• The output of the logistic function is not symmetric around zero, i.e., the value is always positive, which makes training difficult.

4) Tanh Activation Function

Tanh function is very similar to the sigmoid function, with a difference in the output range of -1 to 1. In Tanh, the larger the input, the closer the output value will be to 1, whereas the smaller the input, the closer the output will be to -1 than 0 in sigmoid.

Here is the derivative of tanh function

• The output of the tanh activation function is Zero centered, it helps in centering the data and makes learning for the next layer much easier.

Below are some of the limitations of a tanh function:

• As the gradient value approaches zero, the network suffers from the Vanishing gradient problem.
• The gradient of the function is much steeper as compared to the sigmoid function.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI