
Building Activation Functions for Deep Networks
Last Updated on July 25, 2023 by Editorial Team
Author(s): Moshe Sipper, Ph.D.
Originally published on Towards AI.

A basic component of a deep neural network is the activation function (AF) — a non-linear function that shapes the final output of a node (“neuron”) in the network. Common activation functions include sigmoid, hyperbolic tangent (tanh), and rectified linear unit (ReLU).

More often than not, network builders will come up with new learning algorithms, architectures, and such, while continuing to use standard AFs.
In two recent works I focused on the AFs, asking what would happen if we did change them.
In “Neural Networks with À La Carte Selection of Activation Functions”, I combined a slew of known AFs into successful network architectures. I did so by using Optuna — a state-of-the-art automatic hyperparameter optimization software framework.
So what do hyperparameters have to do with AFs? Well, ultimately, it depends on you, the coder, to define what constitutes a hyperparameter. I “gave” Optuna a list of 48 possible AFs from PyTorch:

Some of these are “officially” defined as AFs (for example, ReLU and Sigmoid), while the others are simply mathematical functions over tensors (for example, Abs and Sin). For good measure, I also threw into the mix 4 new AFs I found in the research literature.
Optuna was given this list to treat as hyperparameters. More precisely, I ran Optuna with 5-layer neural networks and with 10-layer neural networks, and Optuna’s task was to find the best-performing list of 5 or 10 AFs, respectively.
I was able to show that this method often produced significantly better results for 25 classification problems, when compared with a standard network composed of ReLU hidden units and a softmax output unit.
In “Evolution of Activation Functions for Deep Learning-Based Image Classification”, my grad student Raz Lapid and I looked into generating new AFs. We used genetic programming, a potent form of evolutionary algorithm, where graphs are evolved in a process simulating evolution by natural selection.
For example, the following graph:

represents the well-known sigmoid AF.
The evolutionary algorithm was given a set of primitives, from which to compose new AFs:
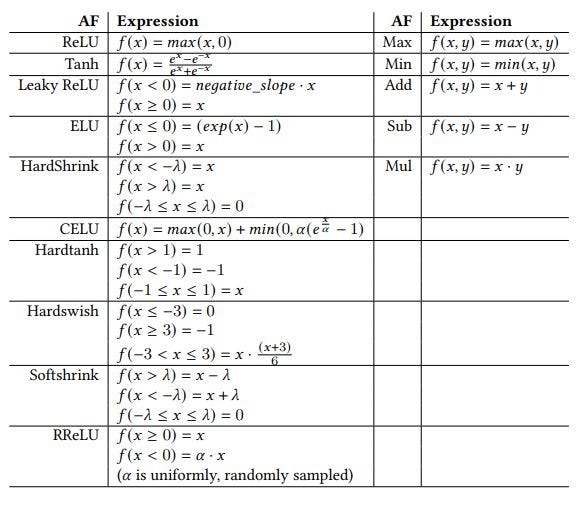
As you can see, we used as basic building blocks standard AFs as well as basic mathematical functions, setting evolution loose to discover novel — possibly potent — combinations. These latter combinations were the new AFs.
We also applied another evolutionary “trick”, using three populations of evolving AFs, rather than one; this is known as coevolution. The idea was to hold a population of AFs for the input layer, another population for the output-layer AFs, and a third population for all hidden-layer AFs. We reasoned that this made sense where neural networks are concerned:

We tested our method on four image datasets and found that coevolution (and “regular” evolution) indeed worked quite well, able to come up with good AFs, which improved network performance when compared with standard AFs. Moreover, our use of different AFs along different network stages proved beneficial.
If you’d like to learn more about evolution, I refer you to a couple of other of my Medium stories:
Evolutionary Algorithms, Genetic Programming, and Learning
Evolutionary algorithms are a family of search algorithms inspired by the process of (Darwinian) evolution in Nature…
medium.com
Evolutionary Adversarial Attacks on Deep Networks
Despite their uncontested success, recent studies have shown that Deep Neural Networks (DNNs) are vulnerable to…
medium.com
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














