Analysis of a Synthetic Breast Cancer Dataset in R

Last Updated on January 7, 2023 by Editorial Team

Last Updated on January 21, 2022 by Editorial Team

Author(s): Dr. Marc Jacobs

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Data Analysis

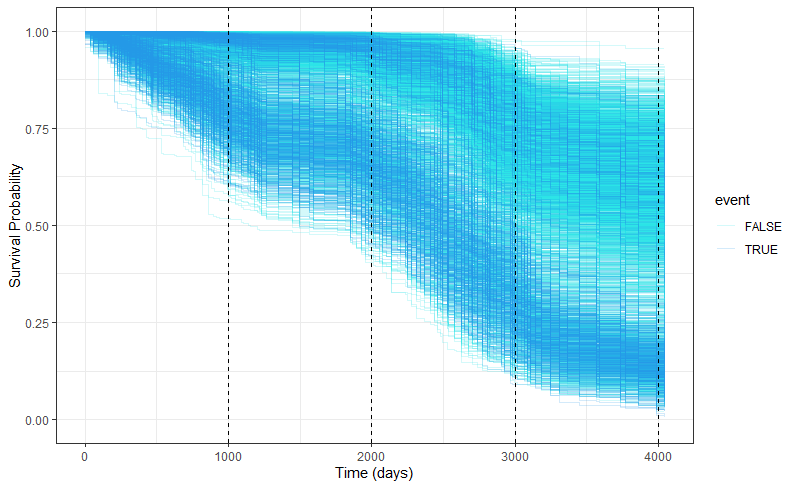
Time-to-event data fully explored

This post is about me analyzing a synthetic dataset containing 60k records of patients with breast cancer. This is REAL data (in terms of structure), but without any patient privacy revealed. The site where you can request the data can be found here and is in Dutch. The great thing about this is that these datasets not only allow us to analyze patient data, without knowing who the patient is but also allow us to test new algorithms or methods on data with a clinical structure. Hence, if you develop something on synthetic data, it will for sure have to merit on (new) patient data.

So, let's get started. The dataset is big and there are many models that can be made. My goal was to explore the data and to build a clinical decision tool based on survival models.

I will show standard graphical exploration, missing data analysis, survival models, and refineries such as penalization.

I hope that this post will inspire more people to dive deeper into this dataset. What I made here is by no means an end-product, nor do I wish it to be. There is just too much there.

Let’s get started!

First of all, I will import the data, explore it from a basic perspective, and then create new variables by refactoring them, combining them, or renaming them.

A lot of data included with many having a completion rate of 100%. Image: by author.

A visual confirmation of a lot of non-missing data. Image: by author.

As you can see, only five variables are really missing most of the time. There are various missing patterns, but nothing exciting. With 60k records, you can play it quite safe. Image: by author.

Further exploration of missing based on certain categorical variables. Nothing that really sticks out. Image: by author.

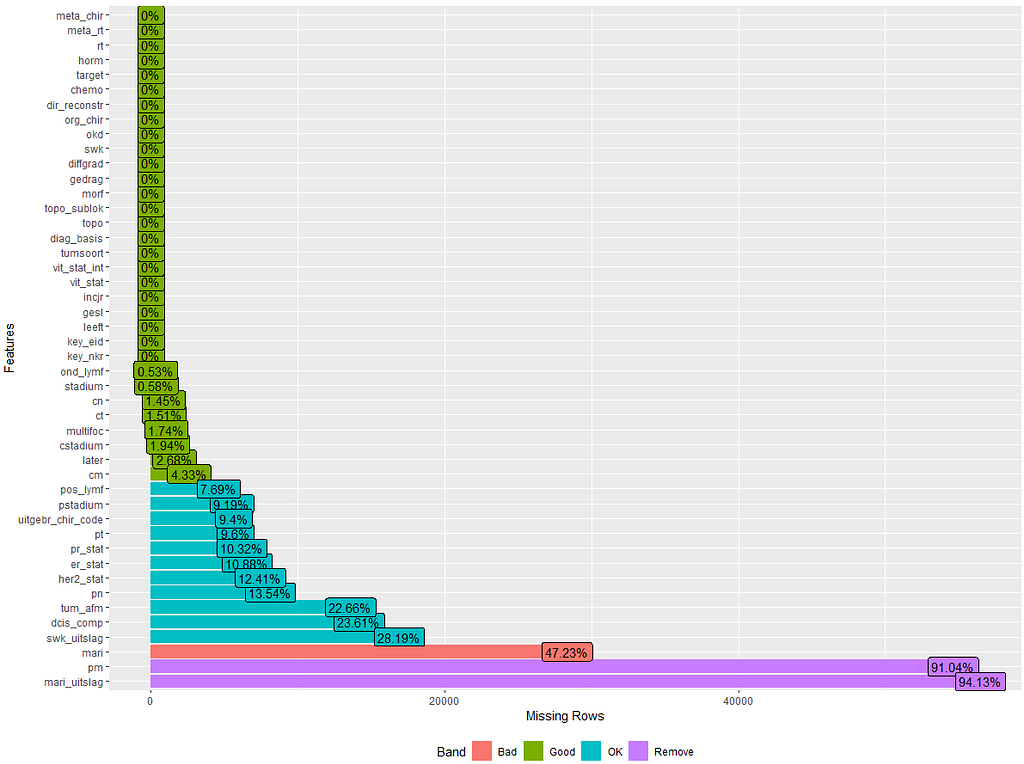
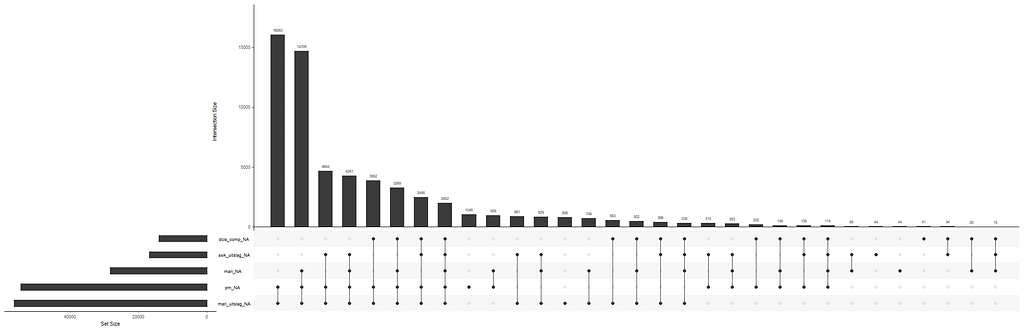
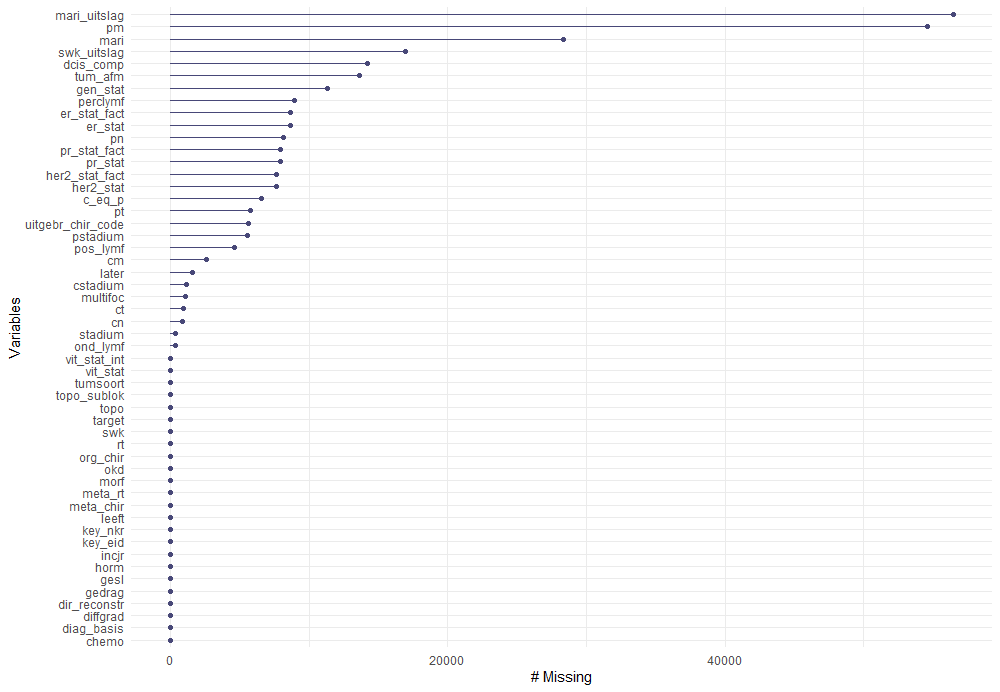
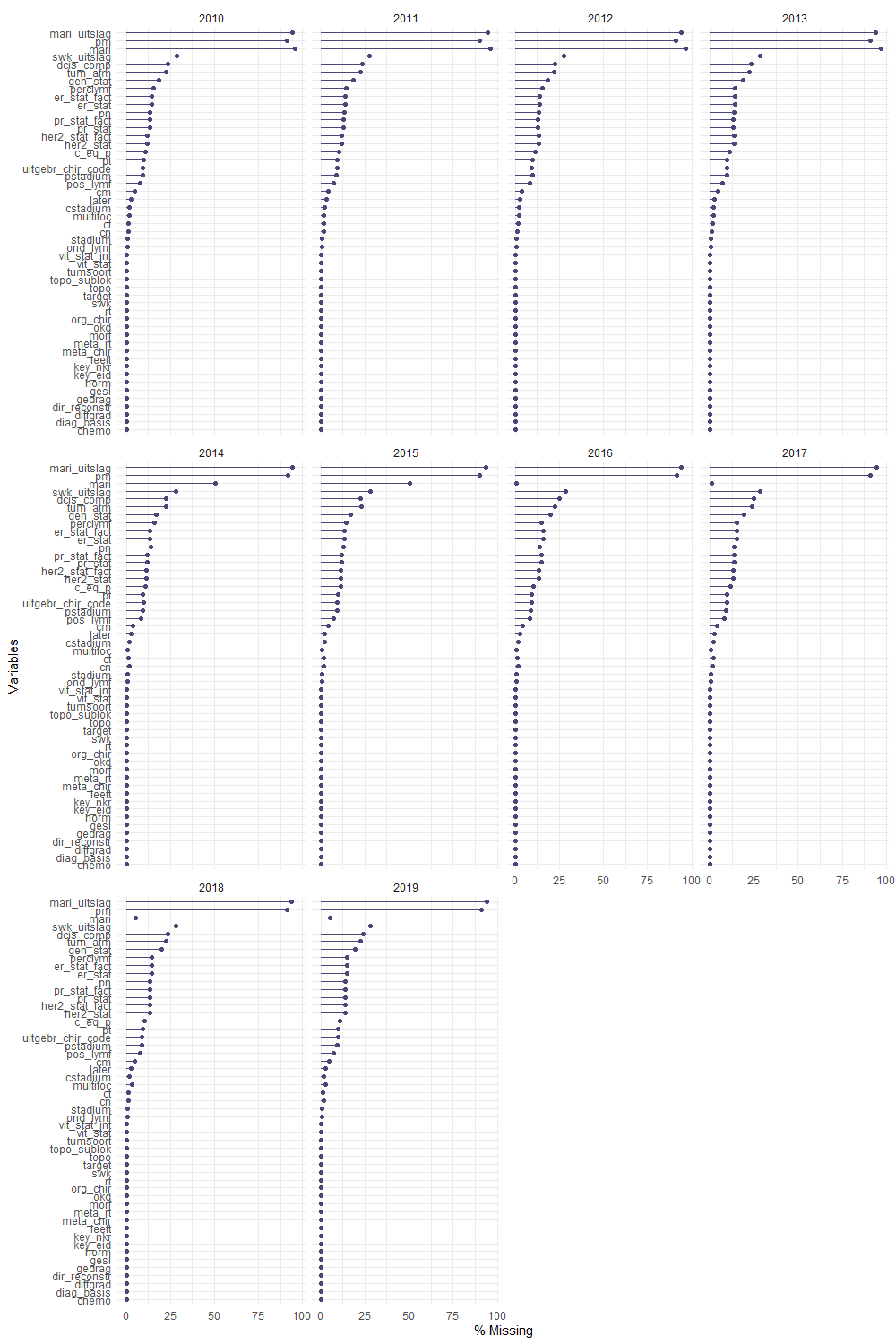
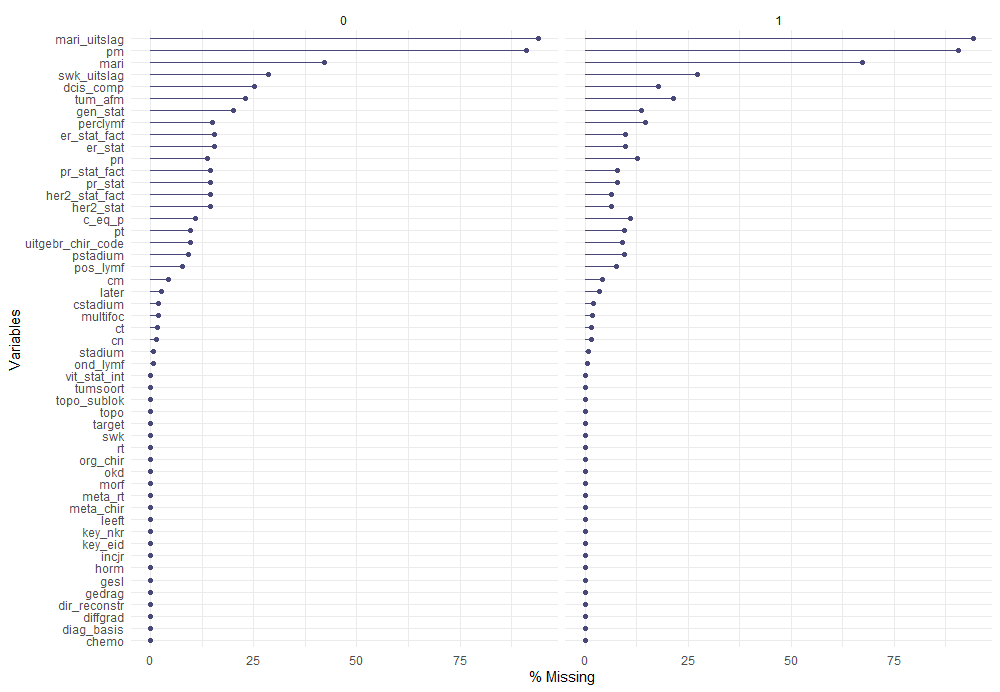
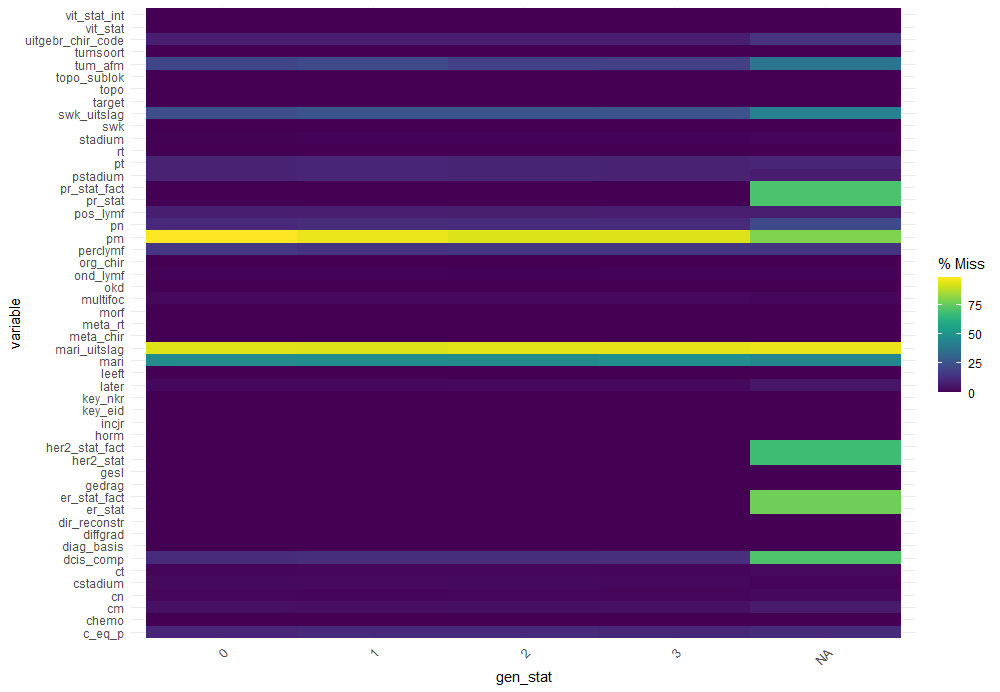
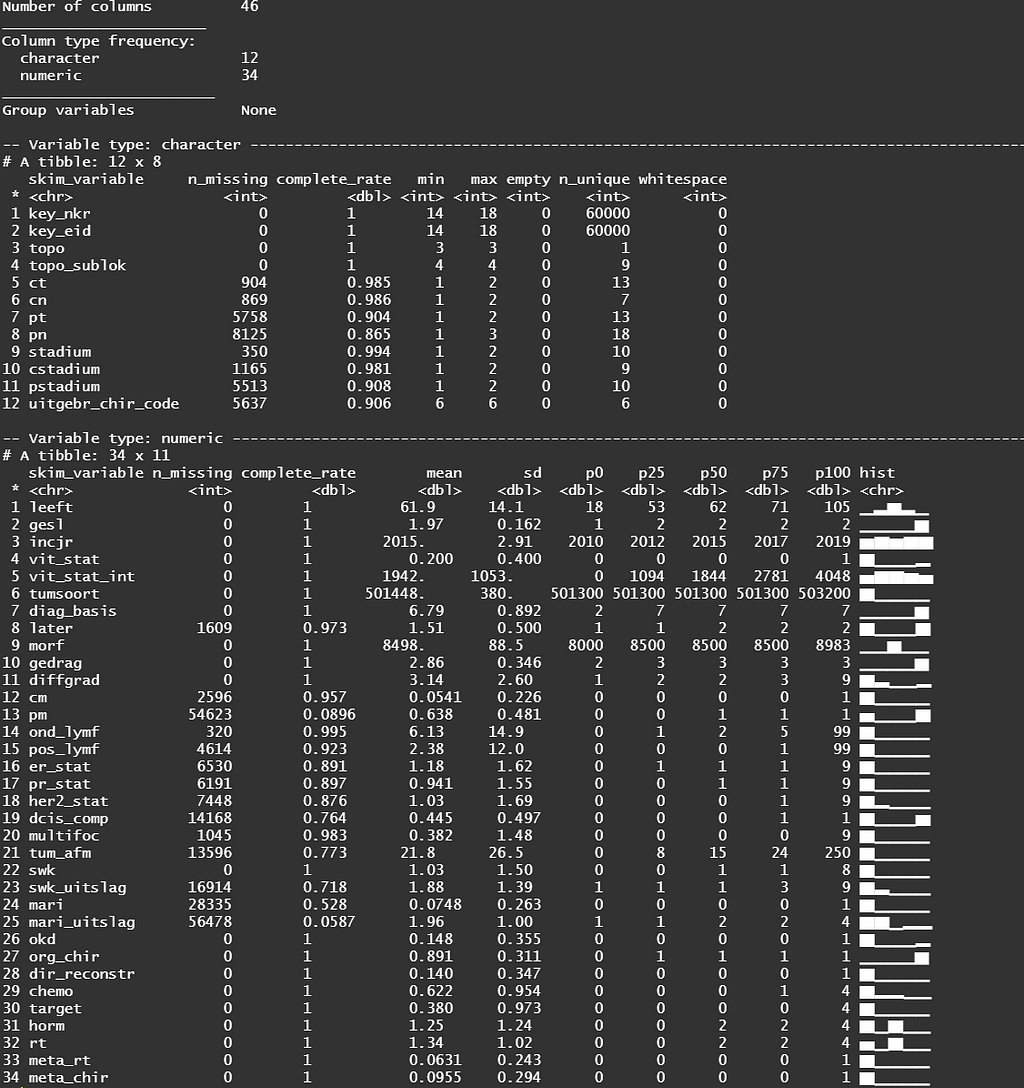
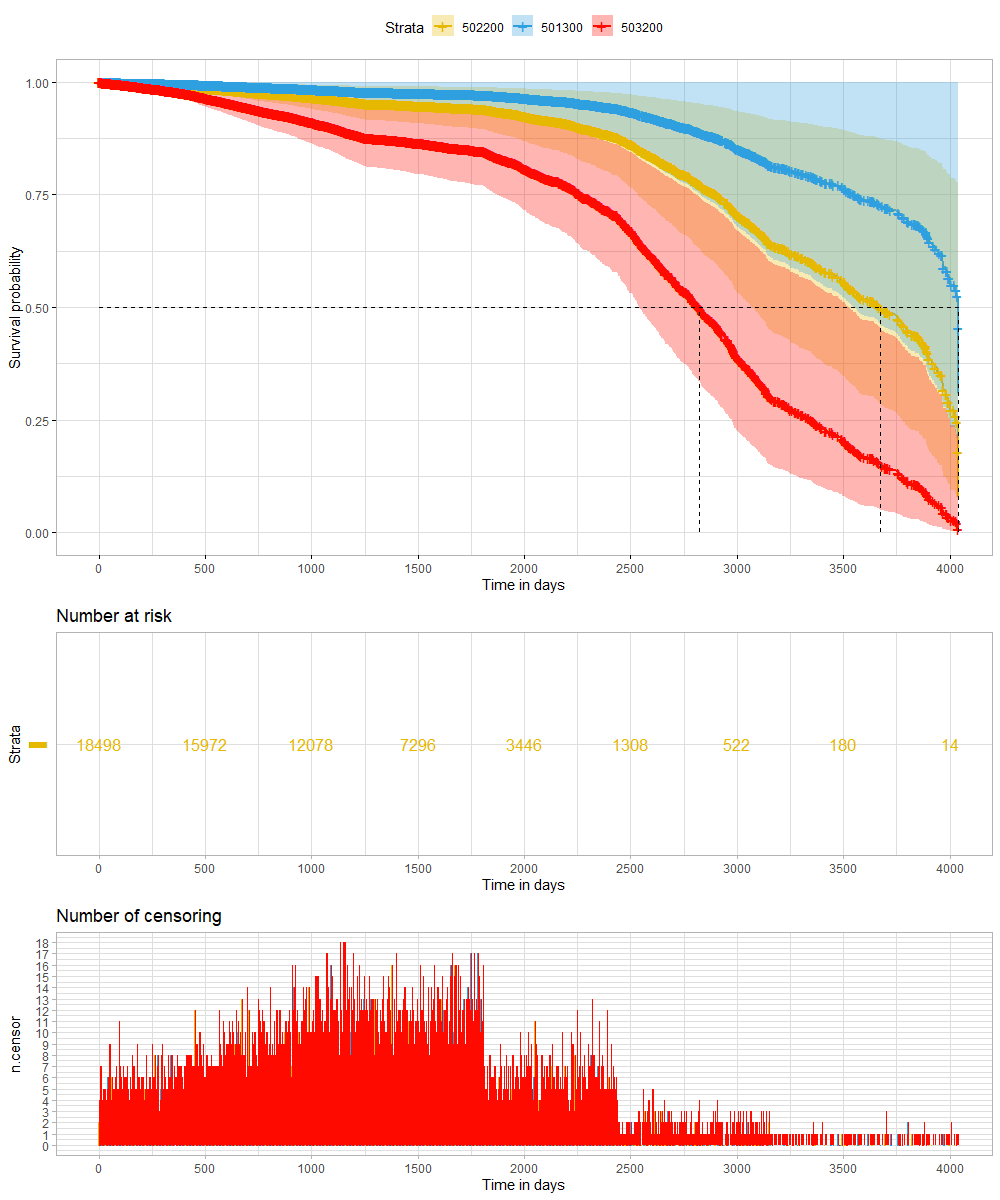
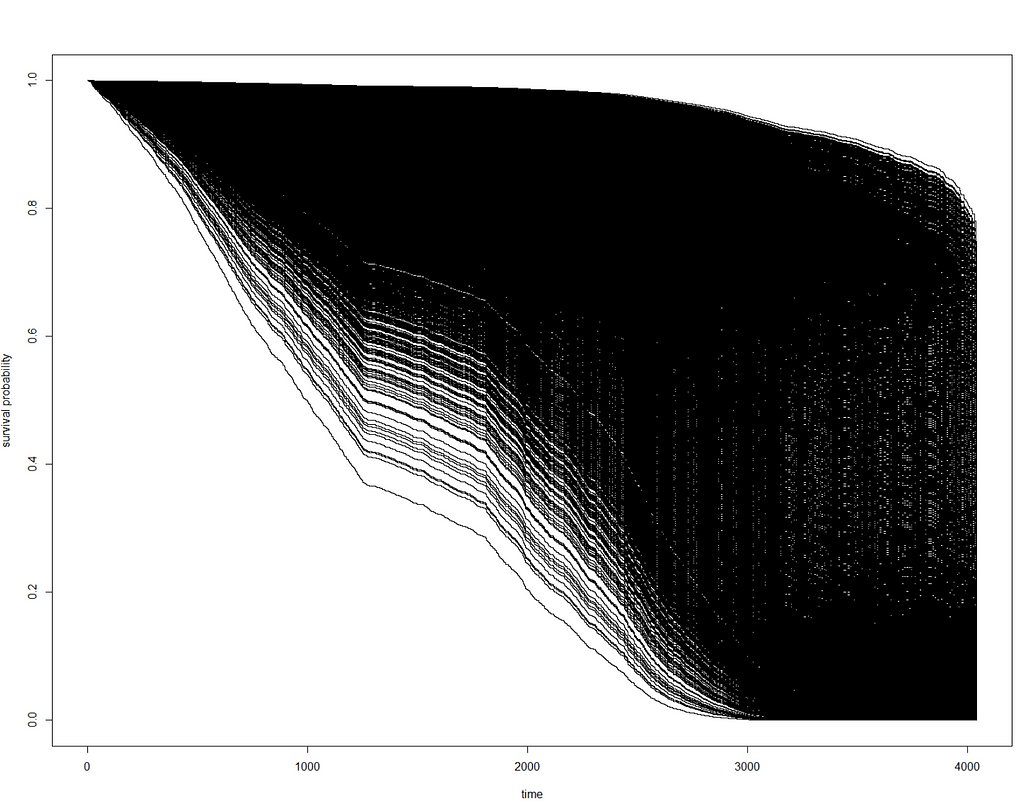
The missing data patterns do not really worry me, so it's time to look deeper into the data. There is a lot, and R does not like me using traditional plots such as points and lines with so many observations. Hence, this is why heatmaps are best, but I cannot resist the urge to dive deeper into the data and still use good old scatter plots.

Different scatter plots that are mainly looking at the relationship between Survival Time, events, and everything in between such as age, sex, tumor size, stage, and lymph nodes investigated. They look nice, but do really help that much. Image: by author.

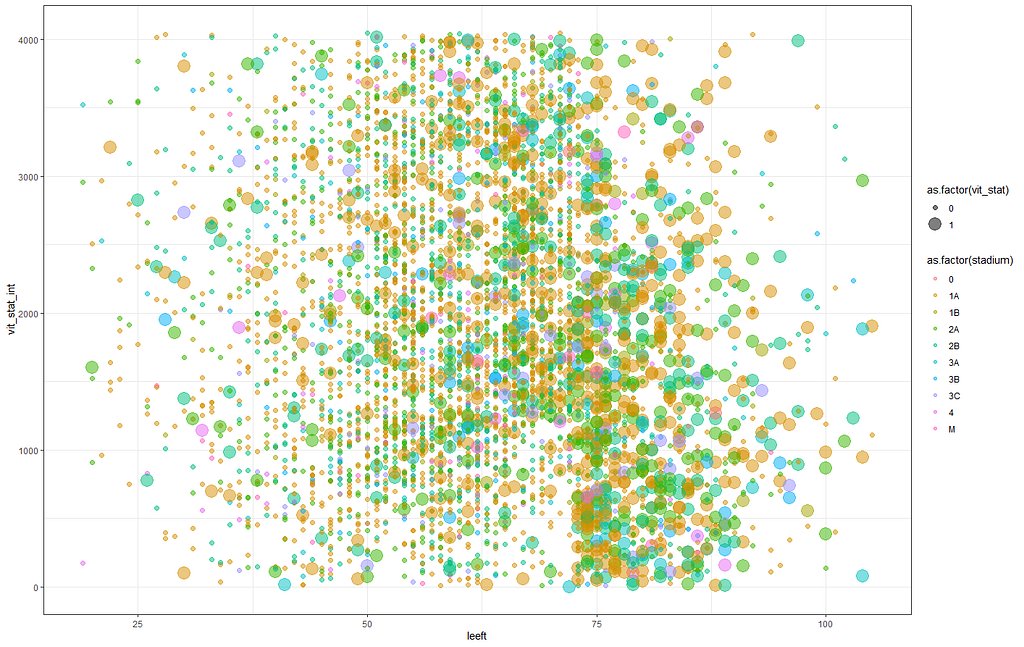
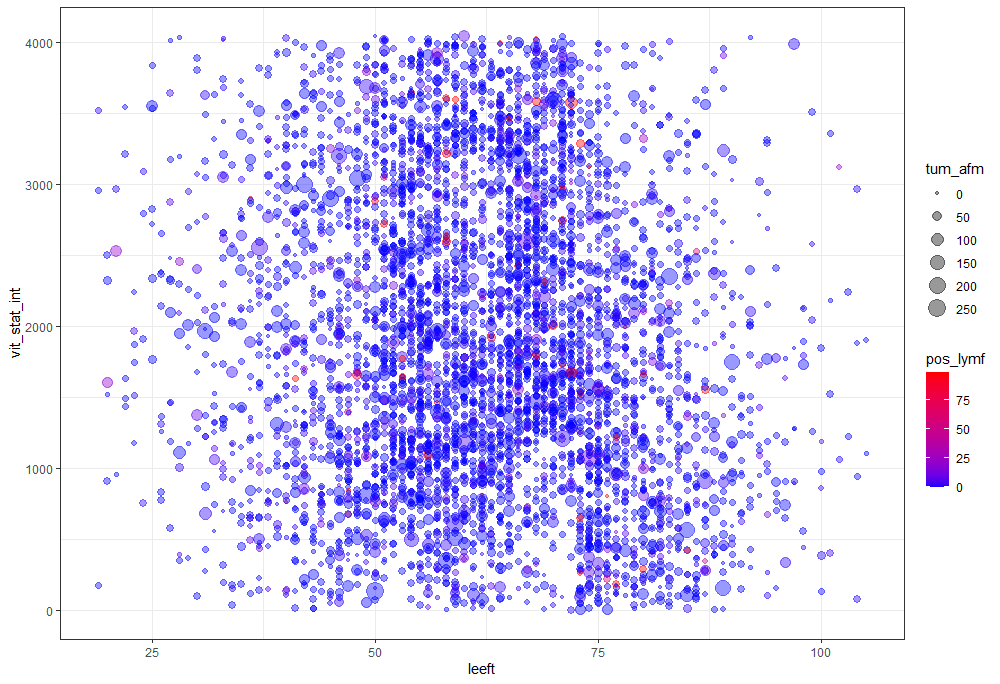
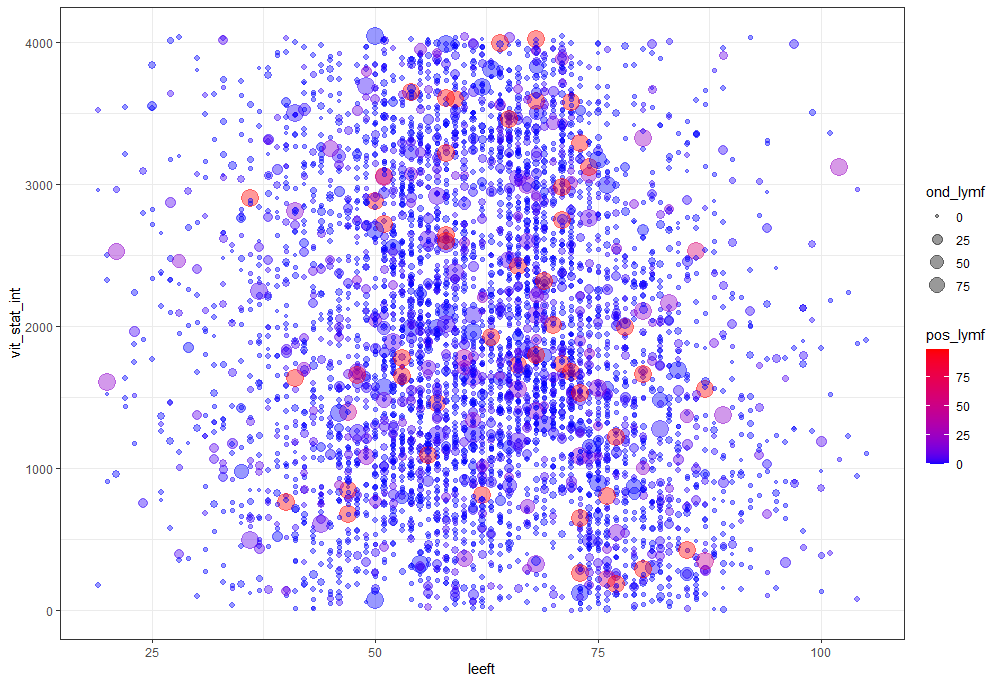
Let's try something more, and a lot else. As you can see, I did not go for the traditional scatterplot matrices, since they have no merit here — 75% of the variables included are categorical variables.

Data per inclusion year. Image: by author.

Survival time by inclusion year. Image: by author.

Survival time by a lot of variables, including the NA option in any of them. It is not so easy to find patterns, although they exist. Image: by author.

Survival time by inclusion year. To be honest, the inclusion year does not help. Although a nice marker for an increase in treatment efficacy, it does not offer much more on top of the survival time itself. Image: by author.

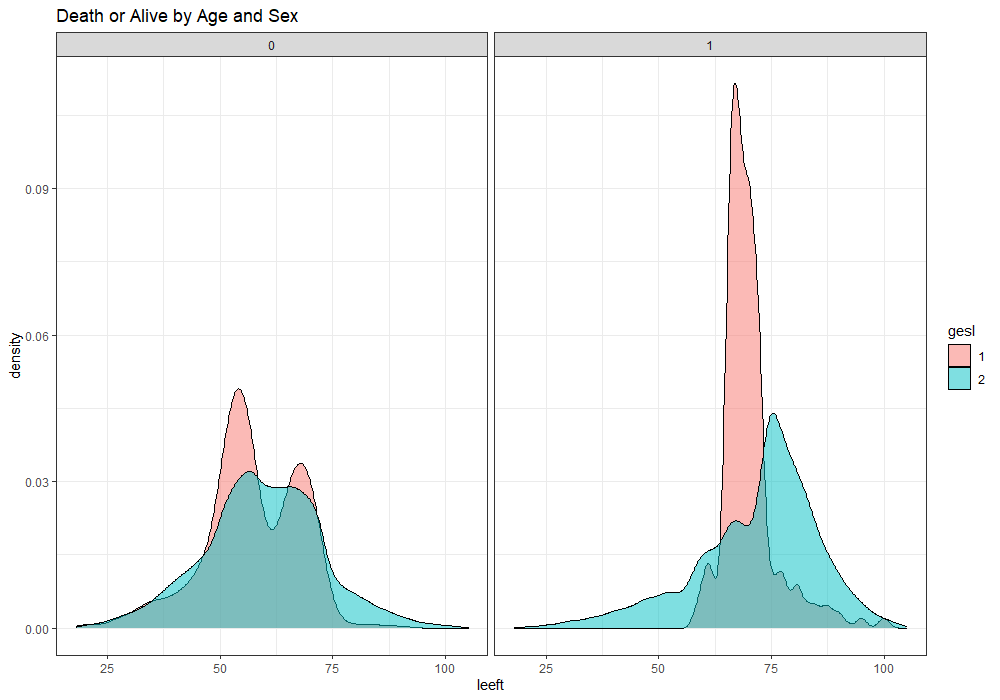
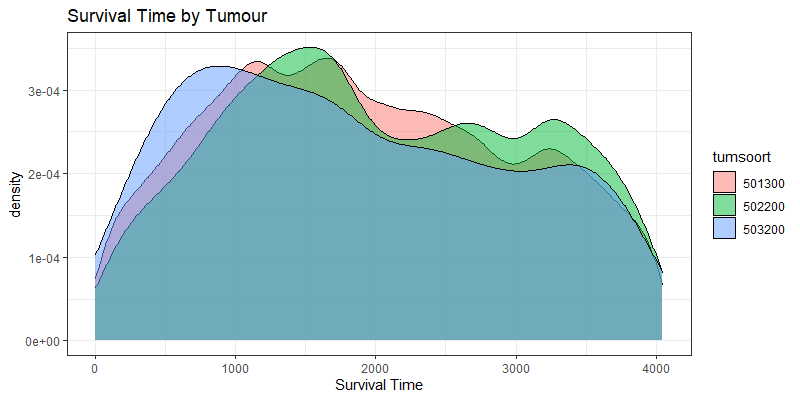
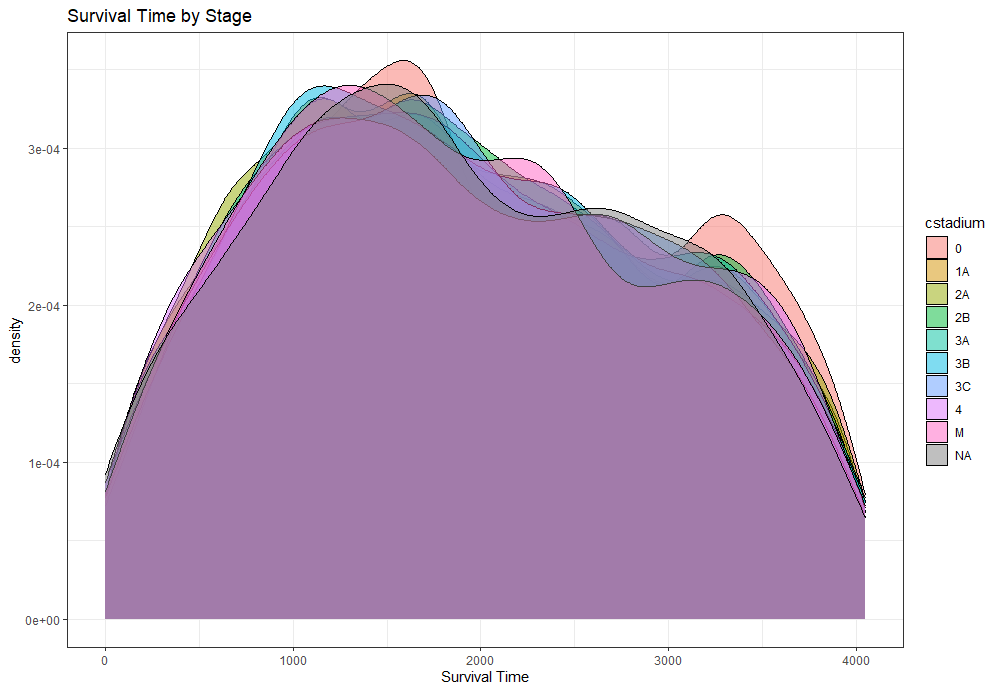
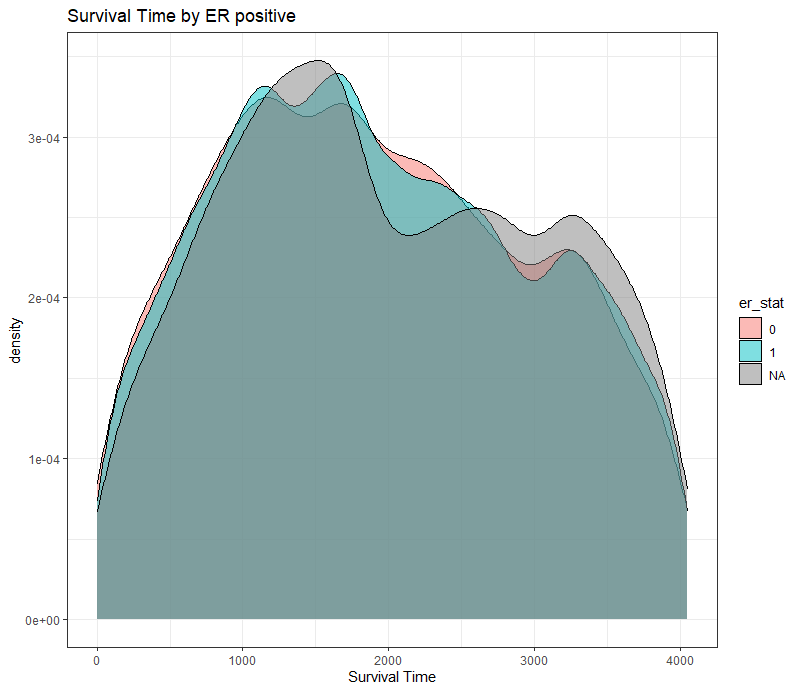
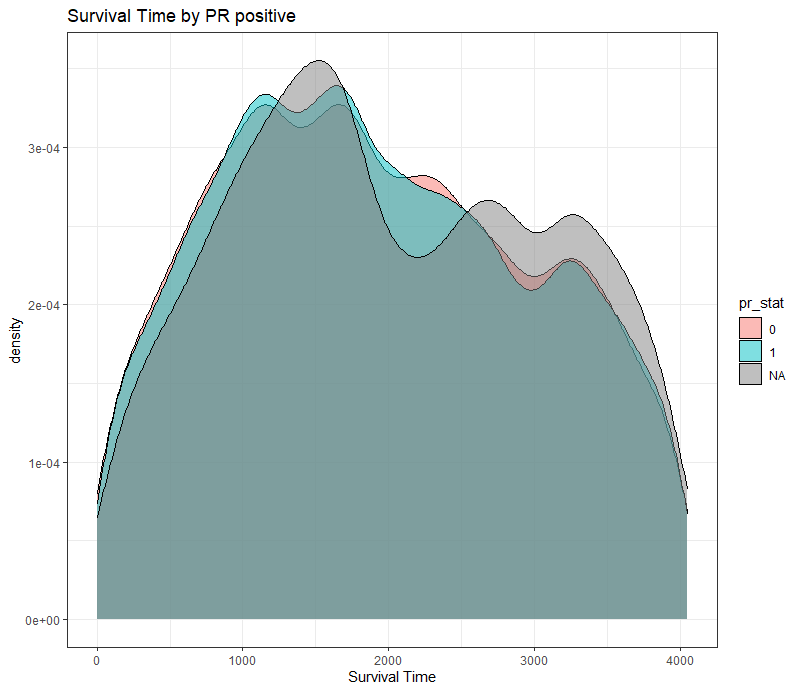
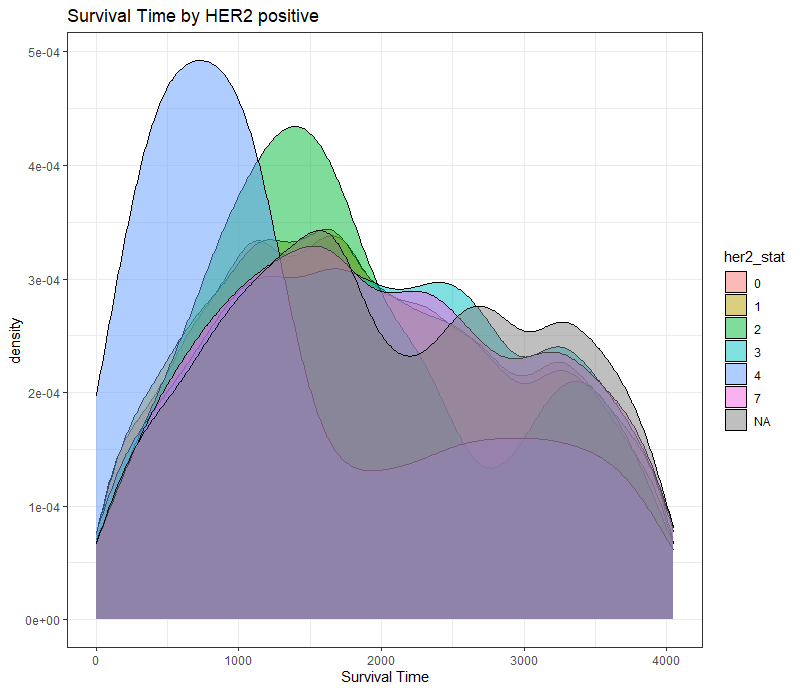
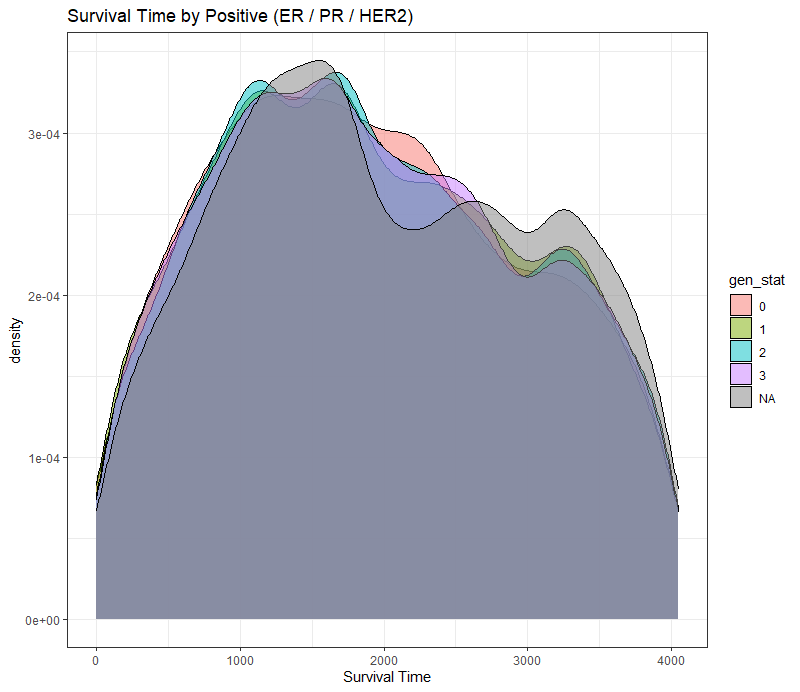
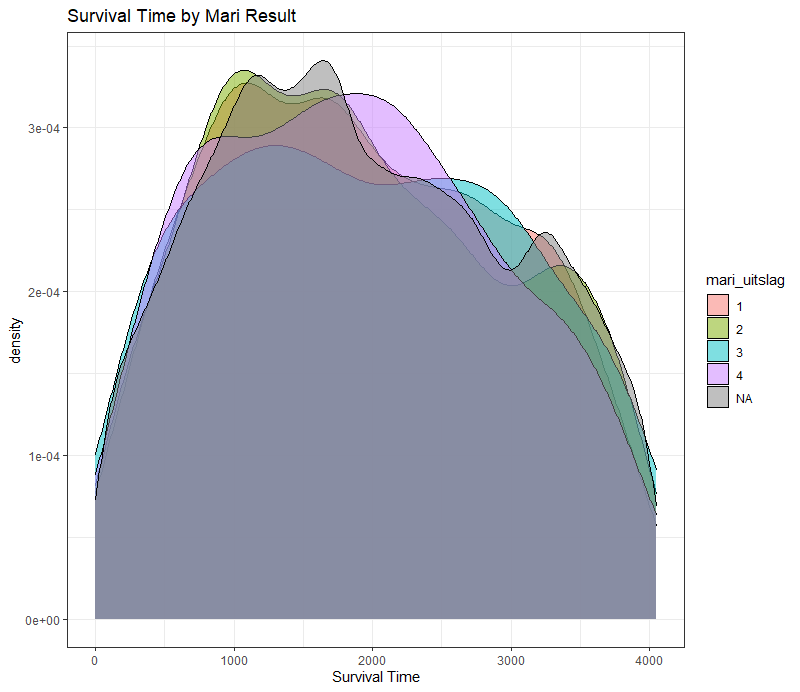
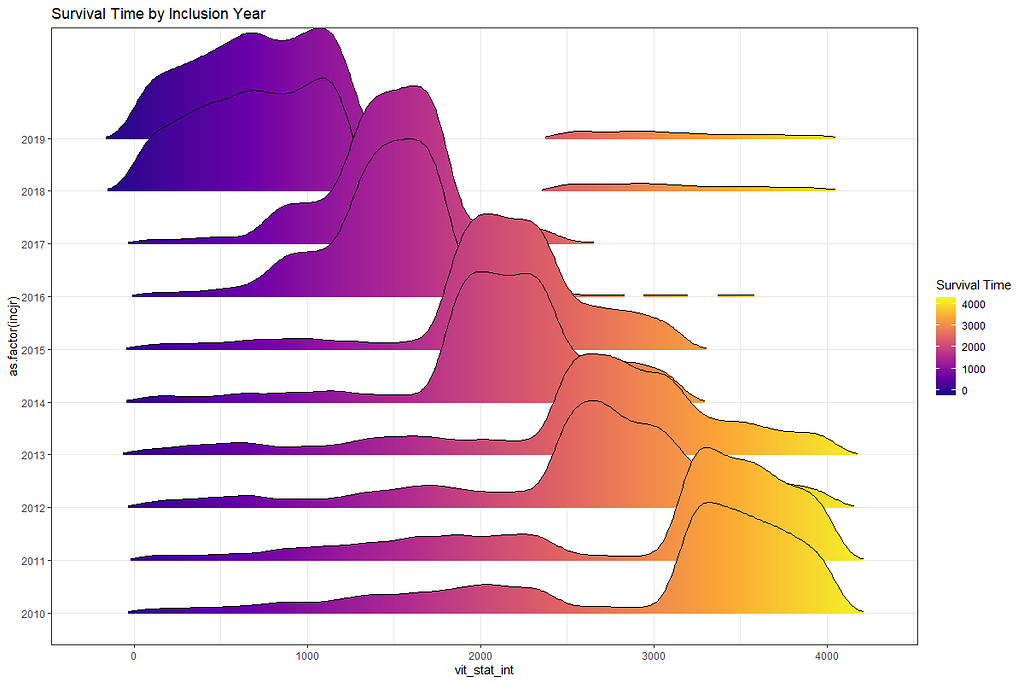
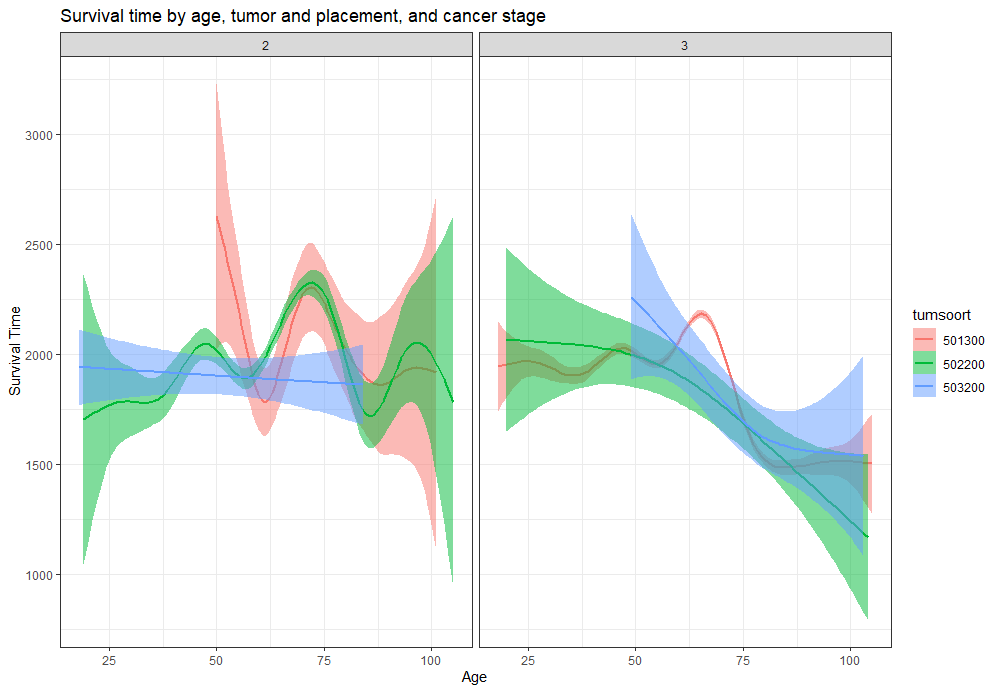
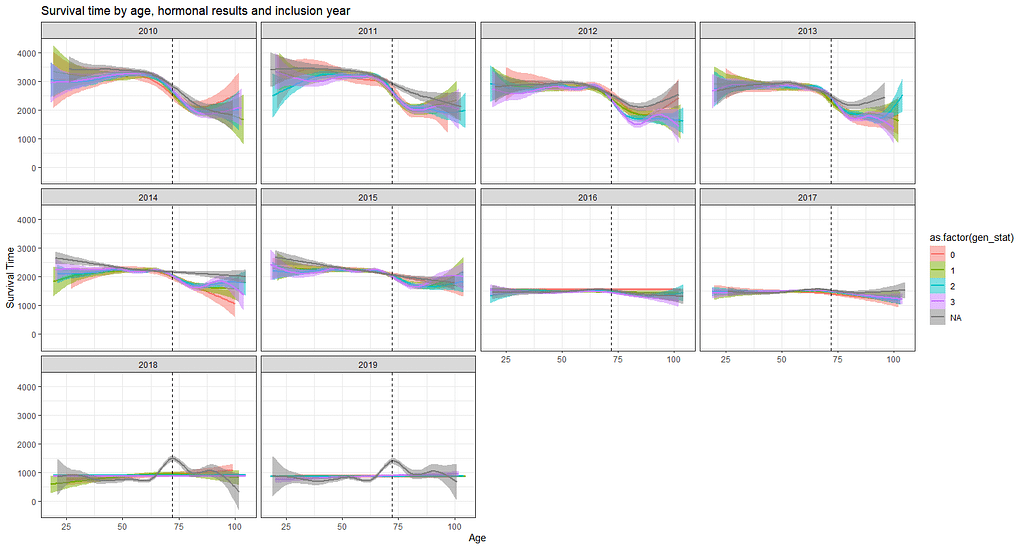
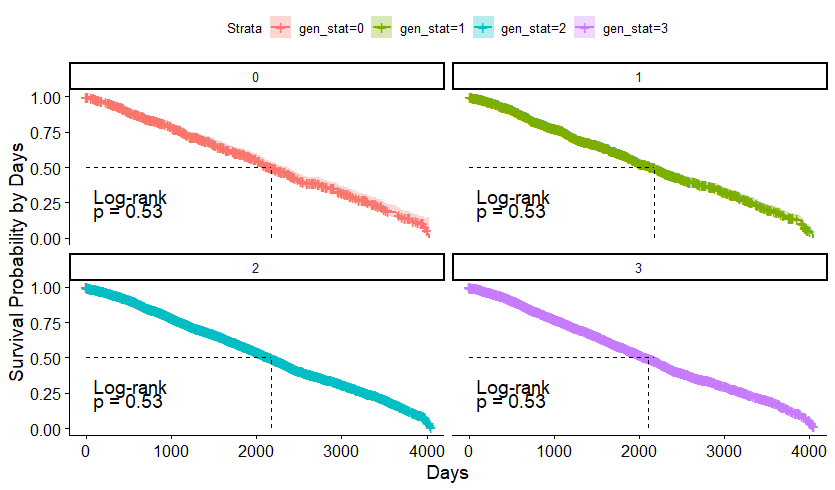
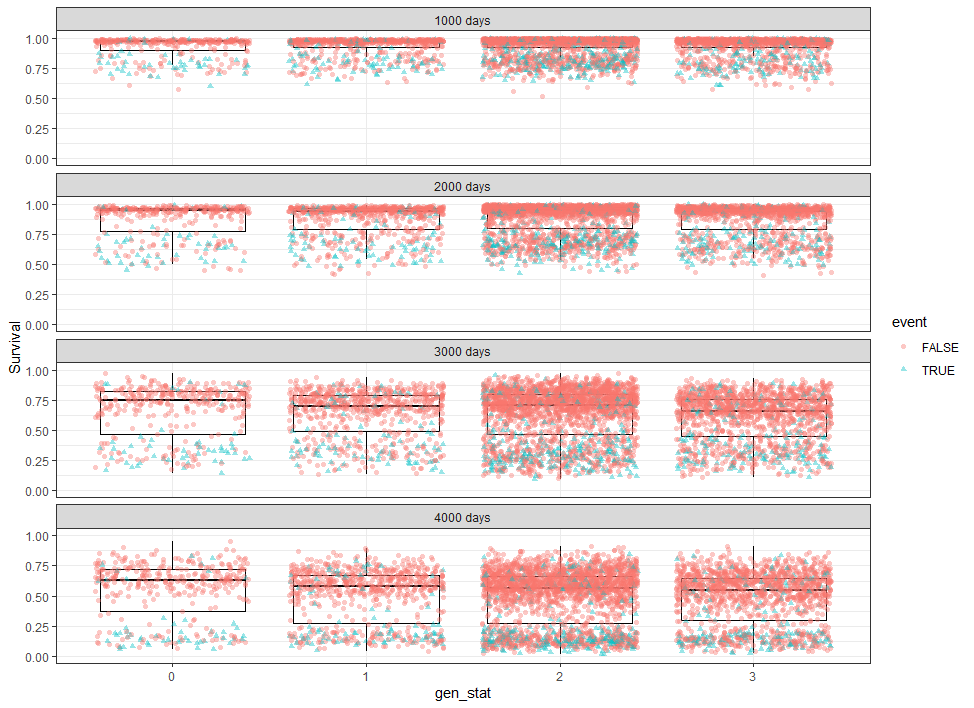
The following graph is trying to show a relationship between survival time, patient age, inclusion year, and a variable called gen_stat which is a combined new variable including the three hormonal markers: her2, er, and pr. If any of these markers were found, regardless of the score, they were labeled a one. Hence, a score of three on gen_stat means that a patient scored positive on all three markers.

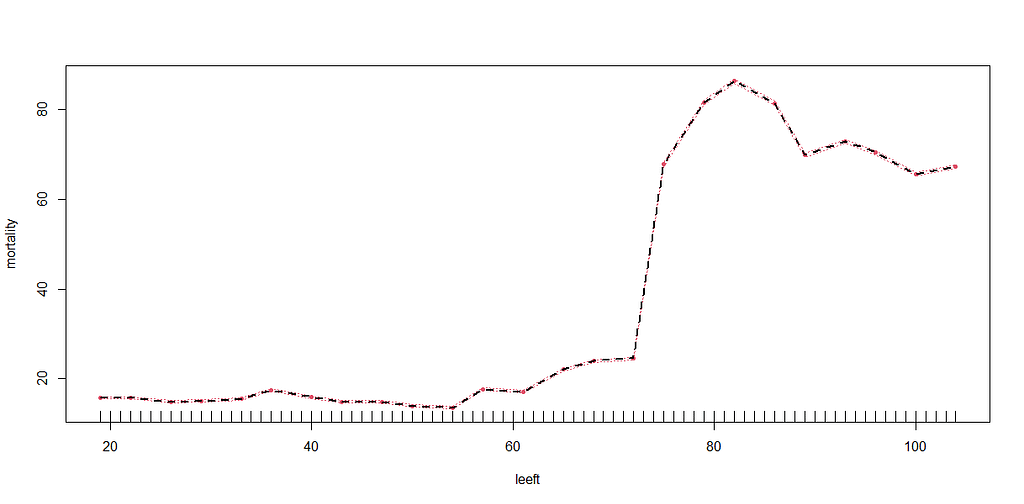
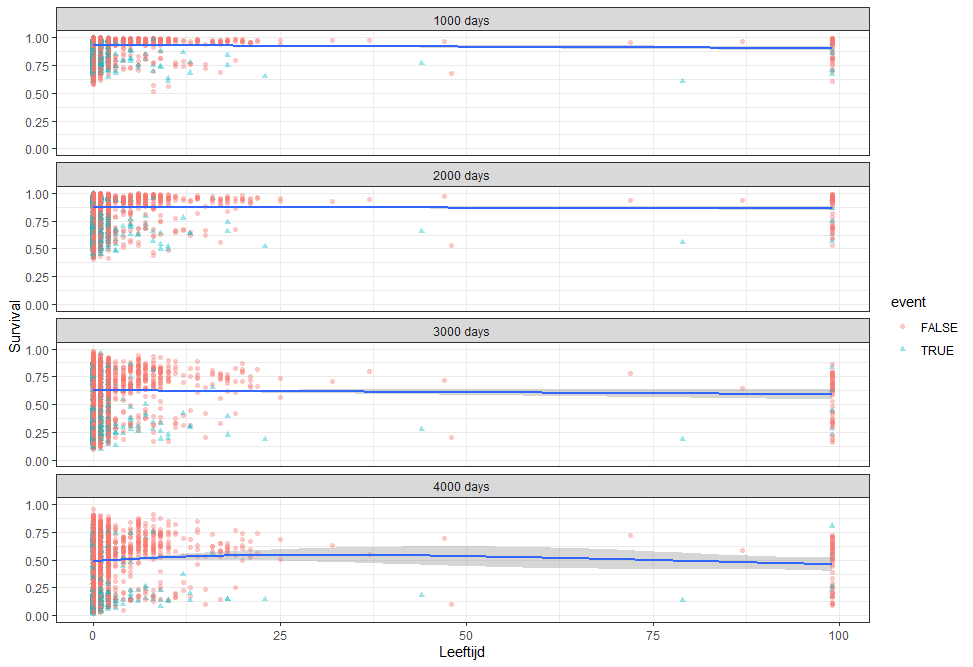
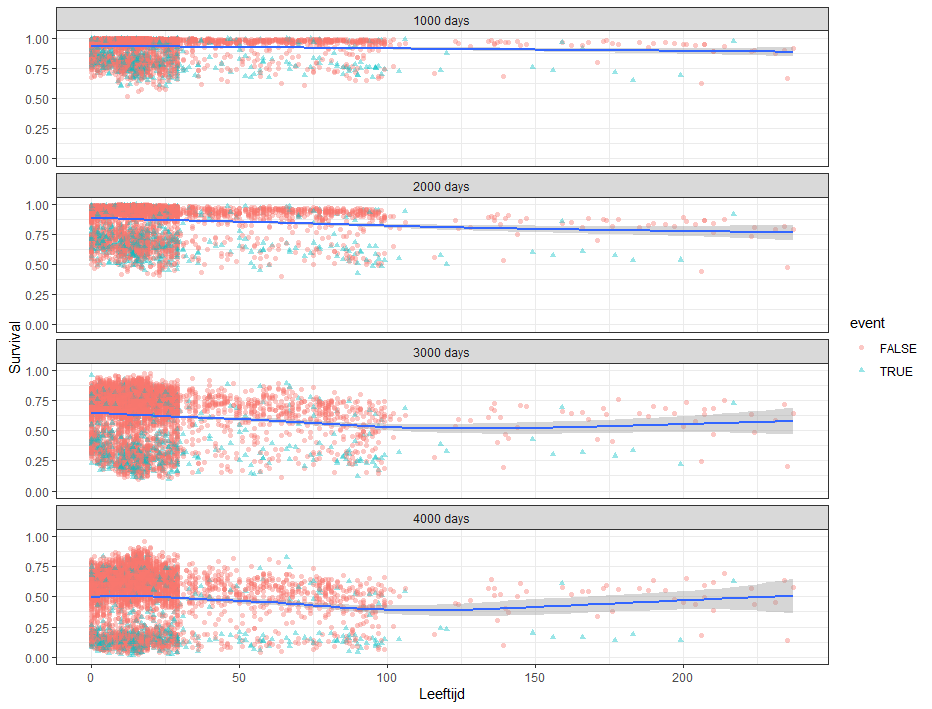
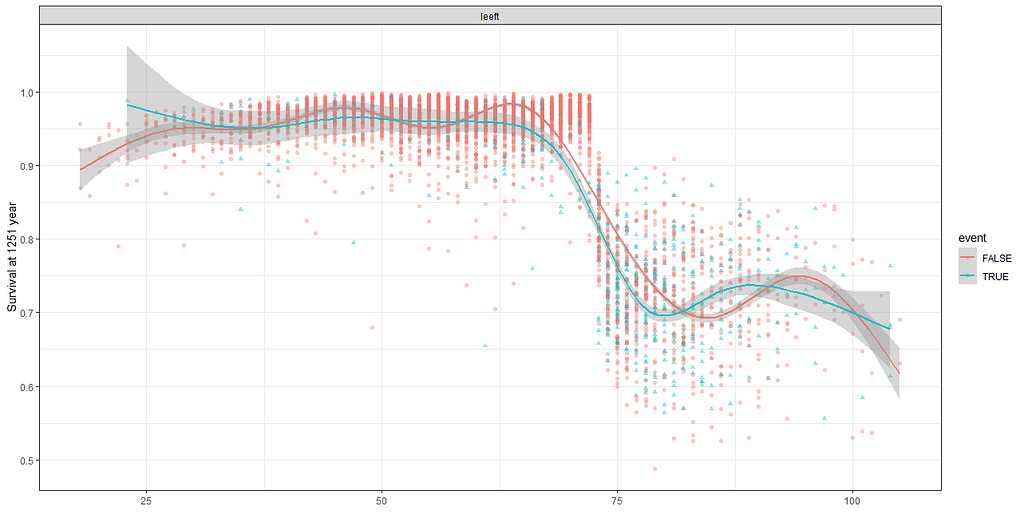
More interesting than those markers is the age of the patient. We will show later that age has for sure a cut-off point.

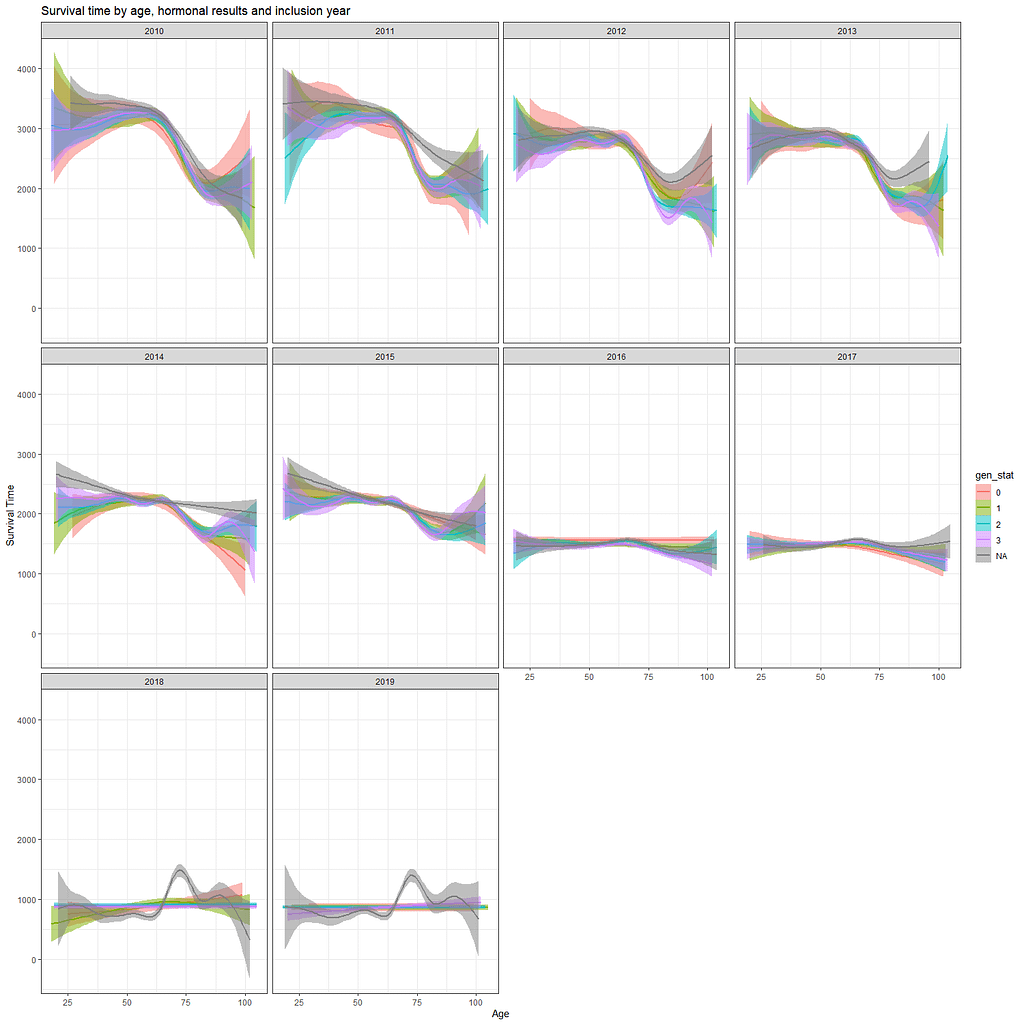
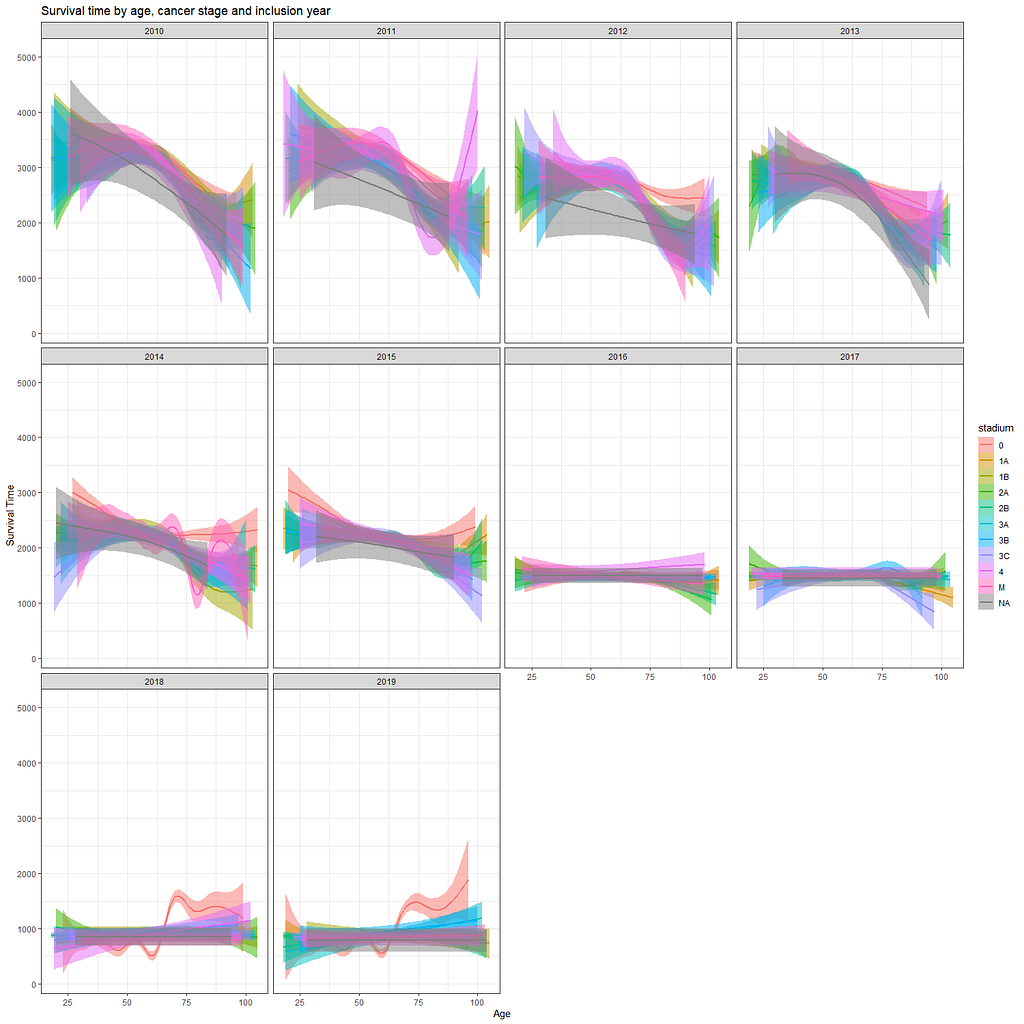
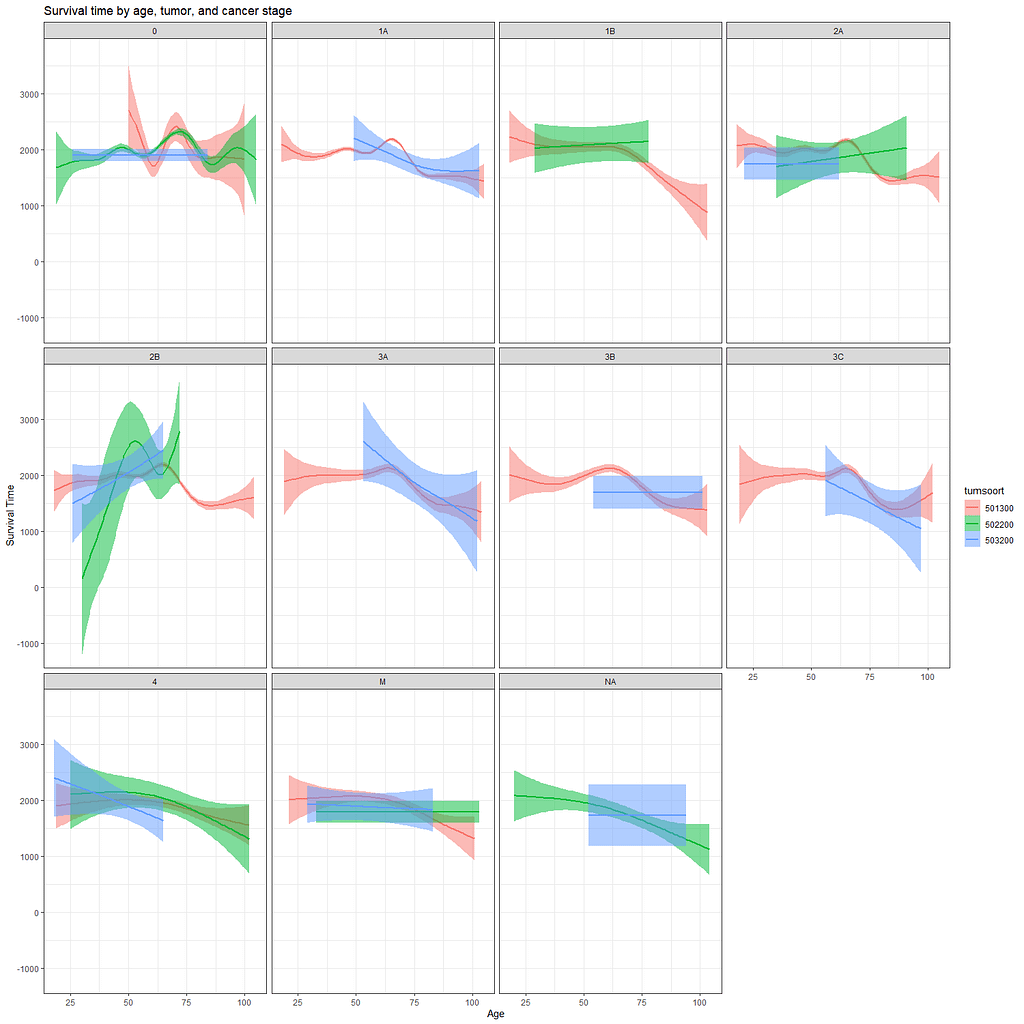
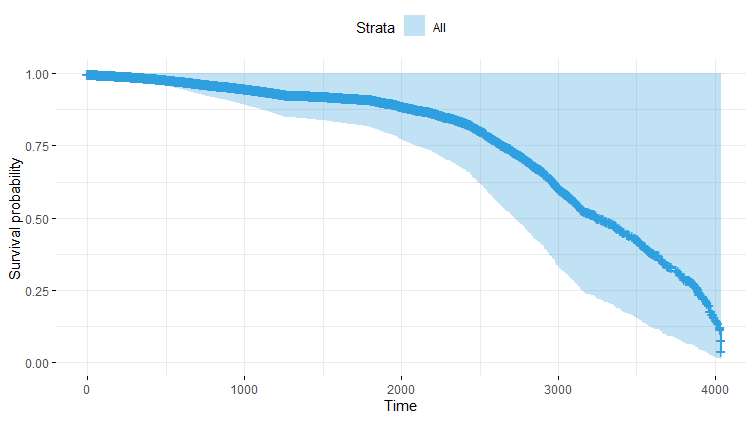
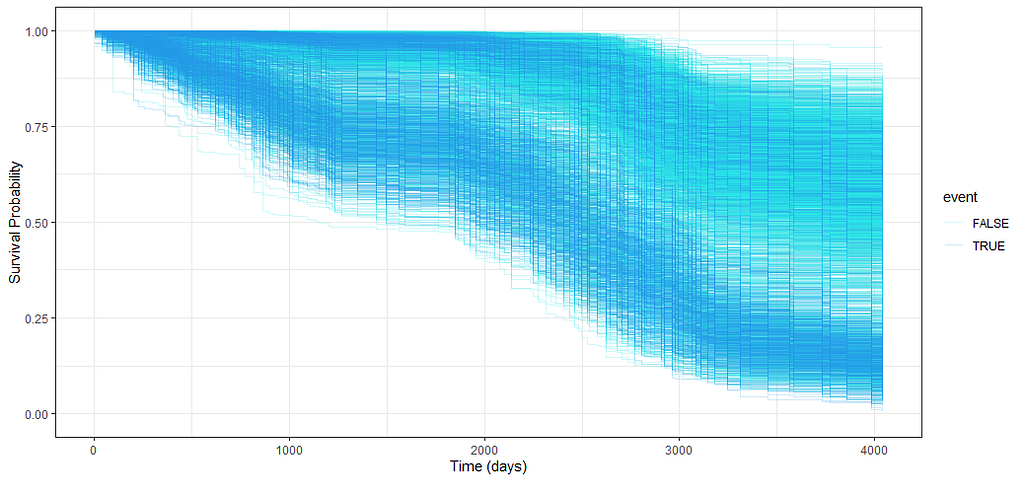
And some spline models on multiple different relationships. Some look really nice, others look funky, which can be quite natural behavior from a spline. Image: by author.

Let's move to the survival analysis itself. This is not the first time I post about conducting survival analysis, and for a deeper introduction please read here and here.

Looks very nice, a lot of data, a lot of events, but a curve that shows very very little. Image: by author.

Clear to see is that the survival curves look good for the earliest included patients, but not so much for the later patients. Breast cancer is disease with a very decent 5-year survival rate. In fact, many are still alive after 9 years. Image: by author.

Here we clearly see a statistical difference, but it is unclear if this is due to real differences in the hazard function or differences in the amount of censoring. Image: by author.

Splitting survival curves by inclusion year is really not a good idea — inclusion year is just a proxy for the length of the survival curve. Image: by author.

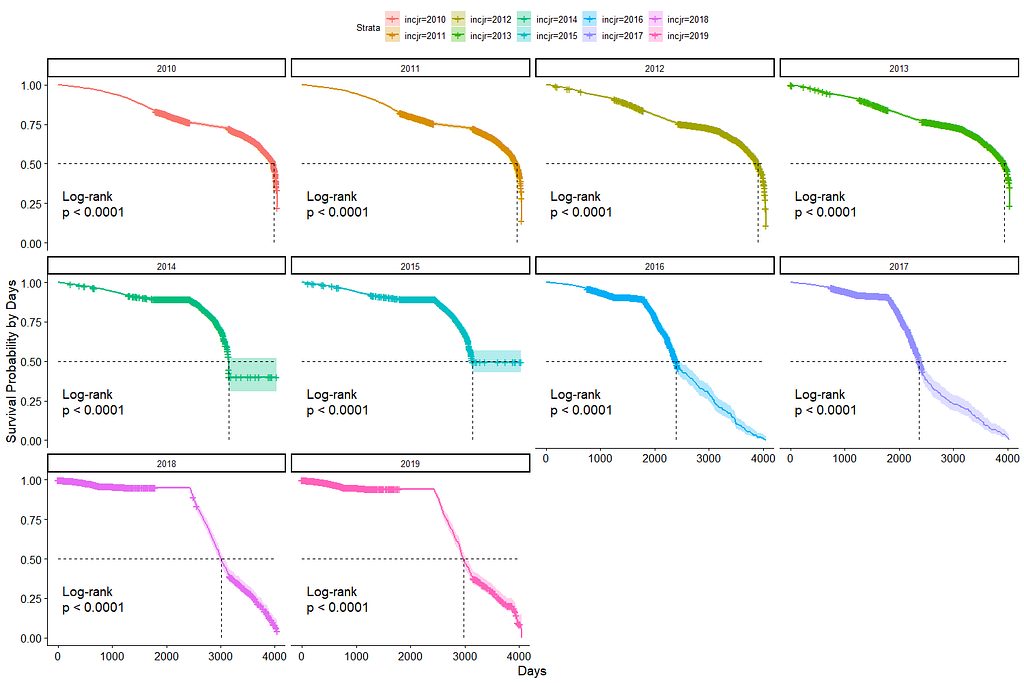
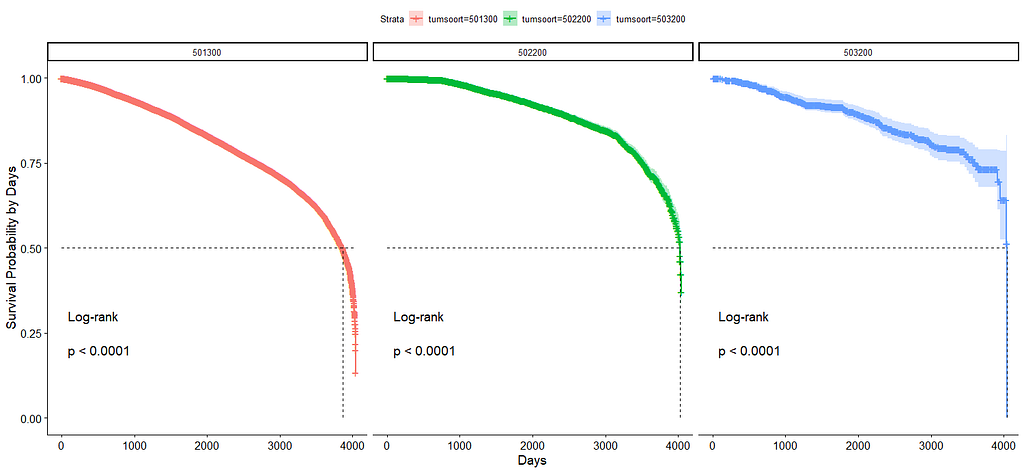
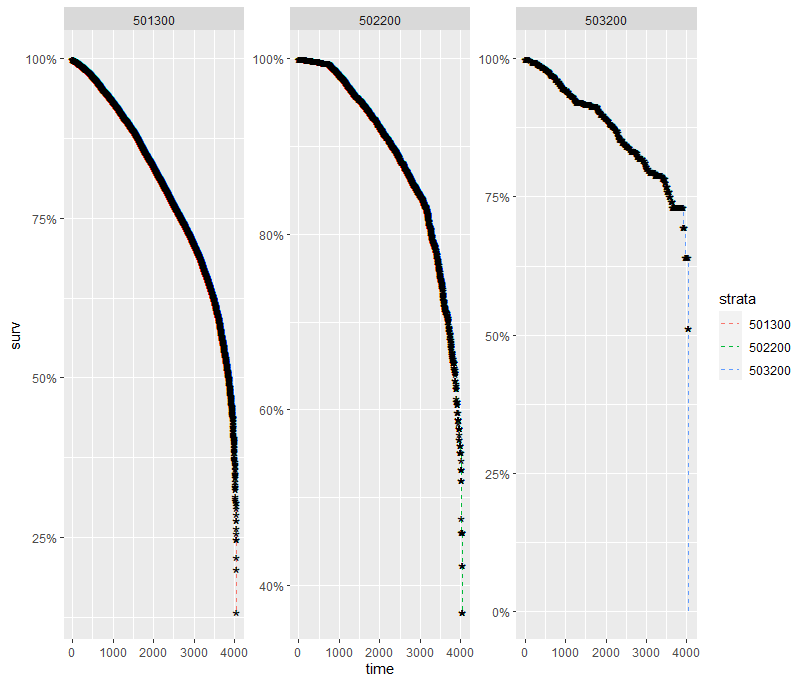
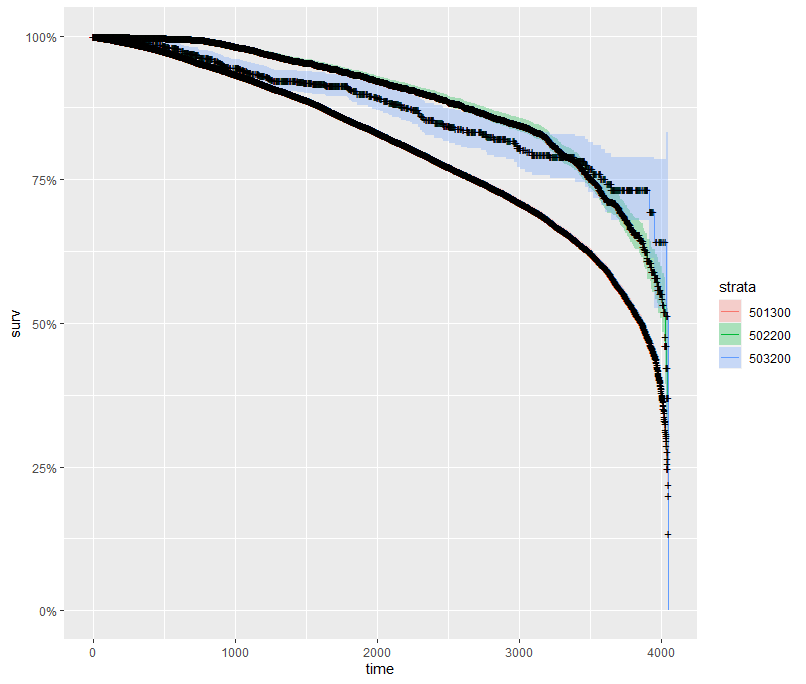
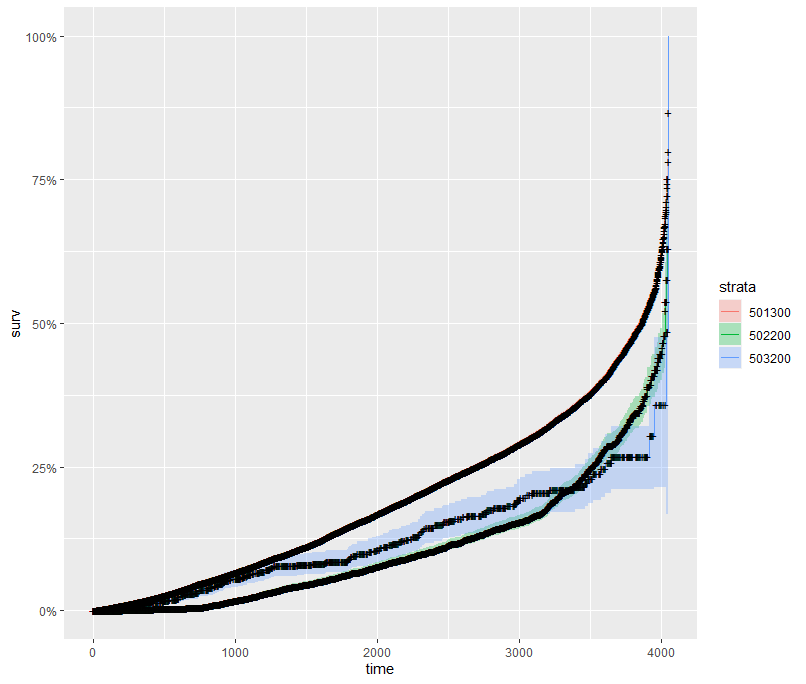
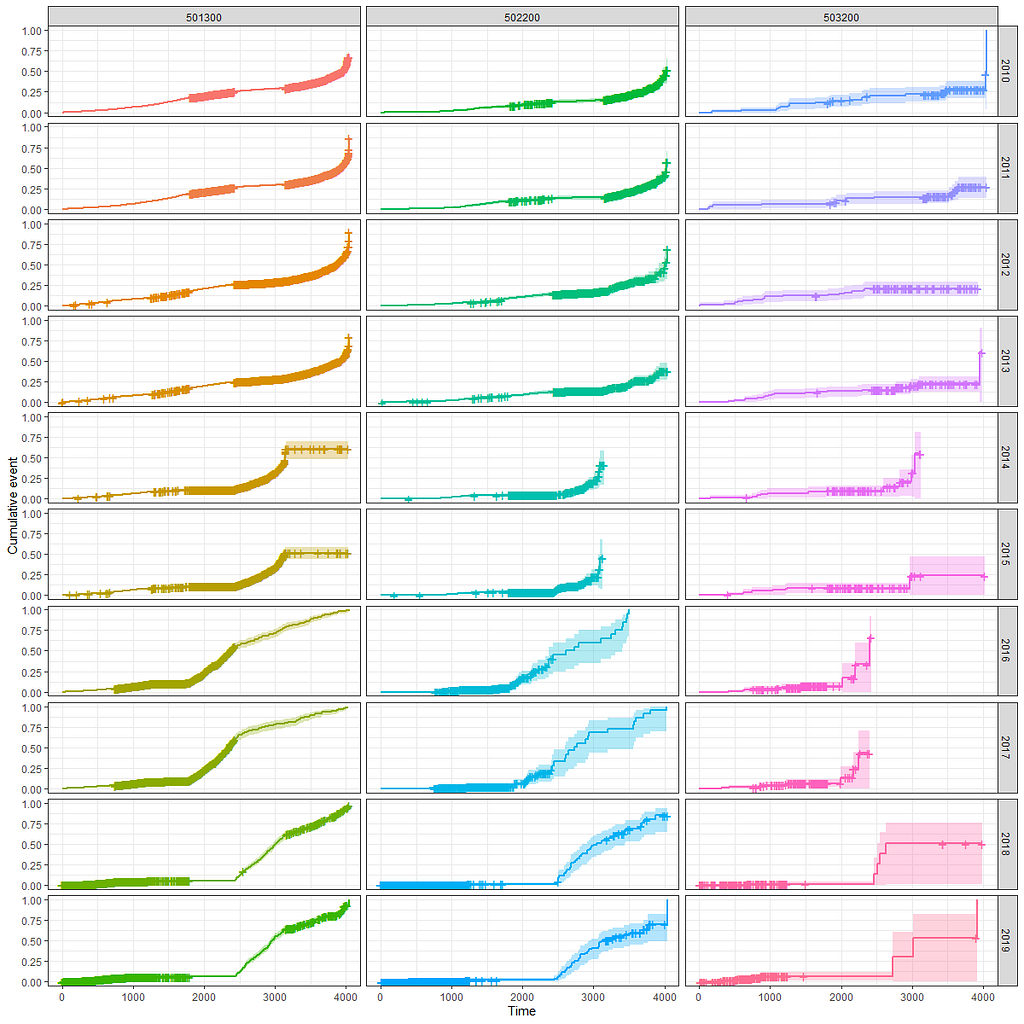
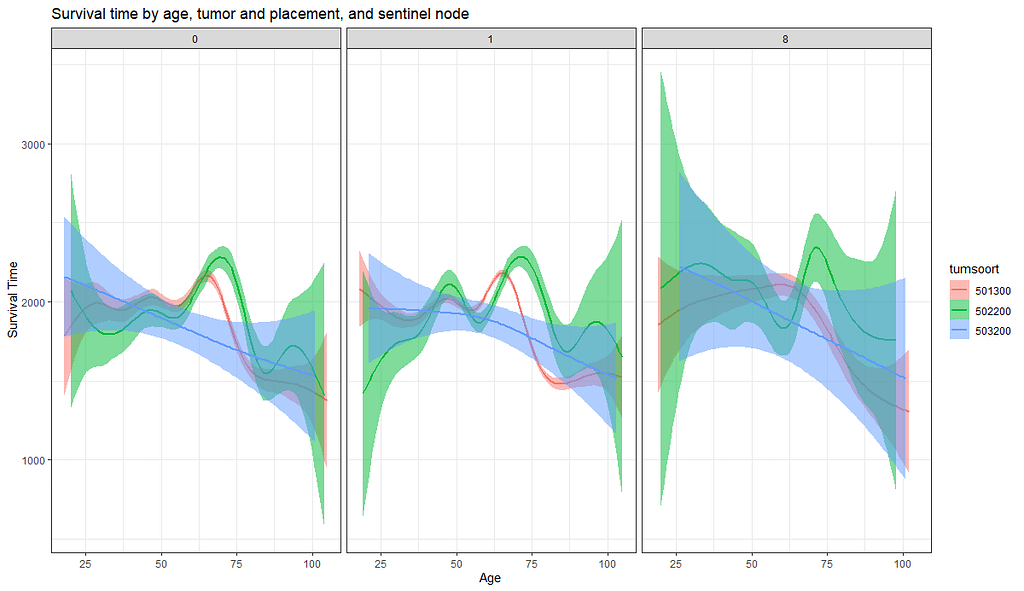
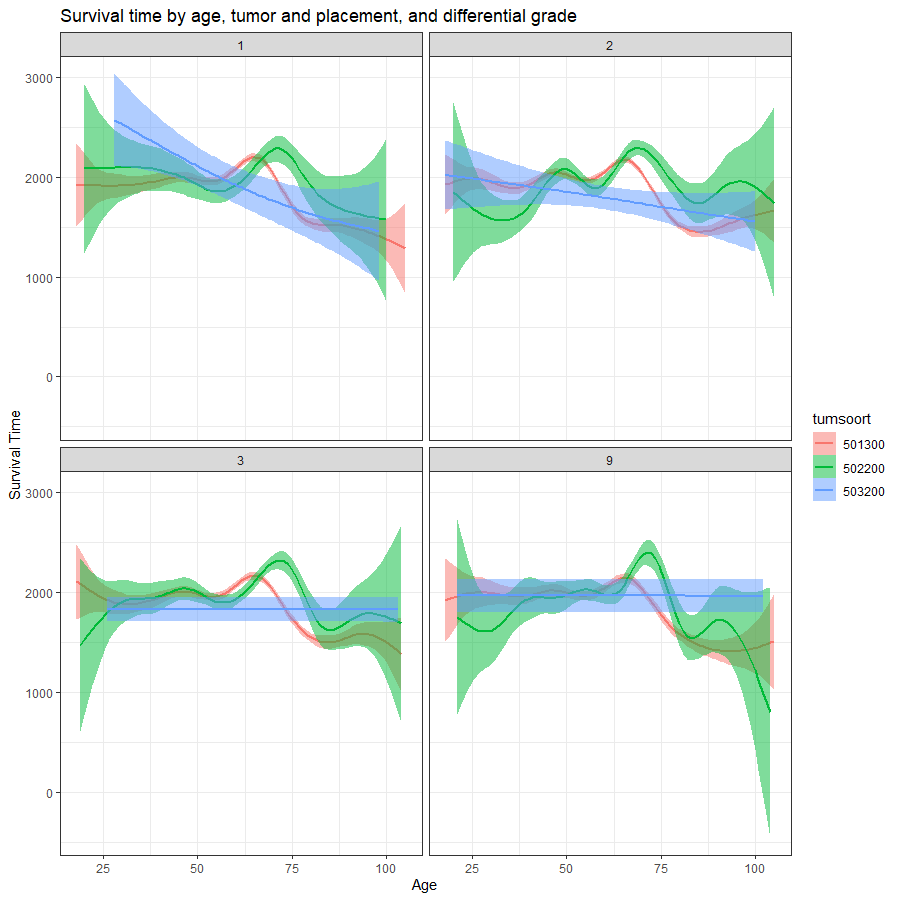
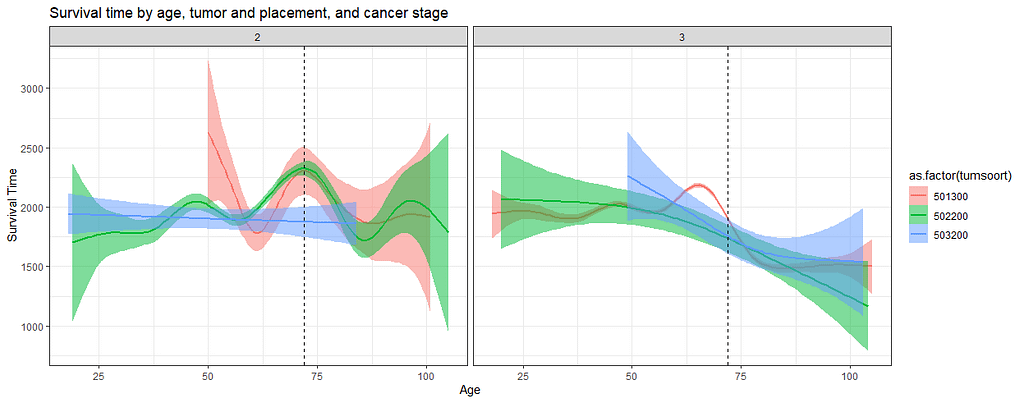
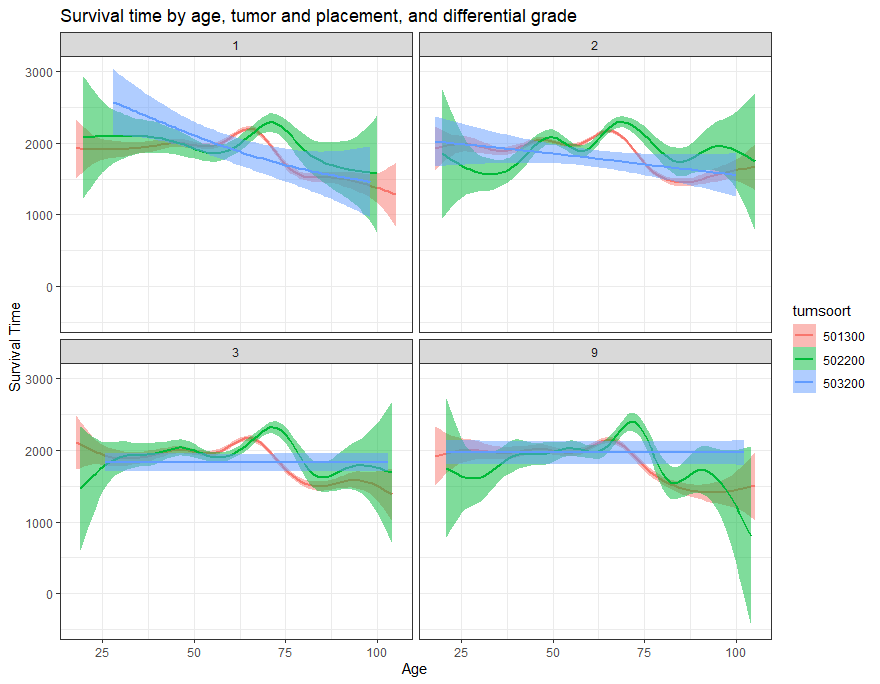
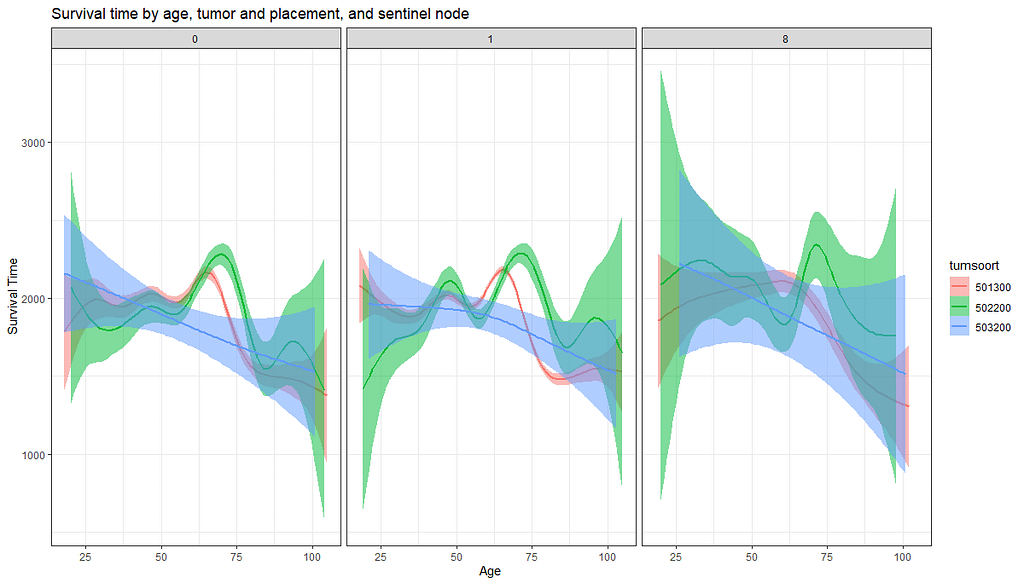
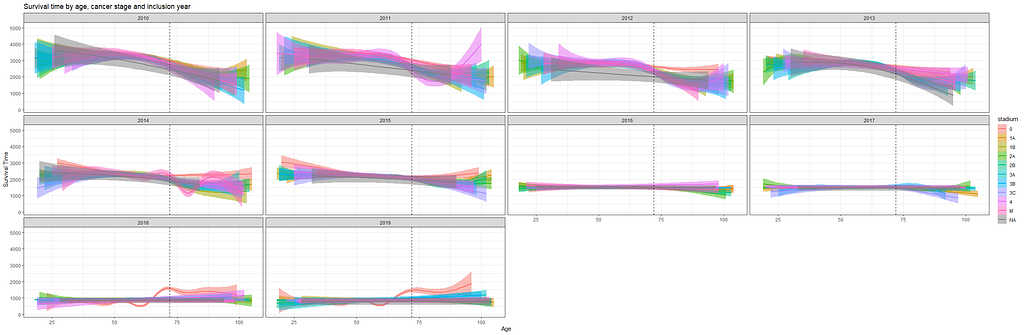
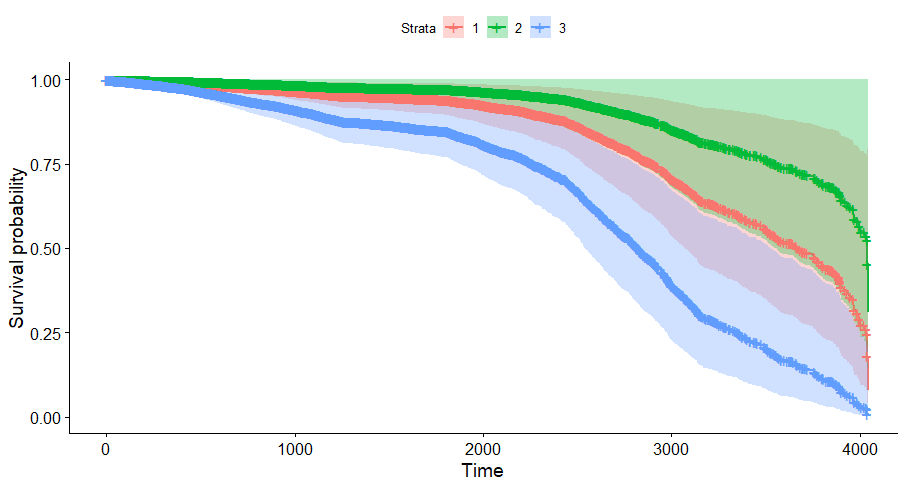
And then I started splitting by almost every imaginable variable included.

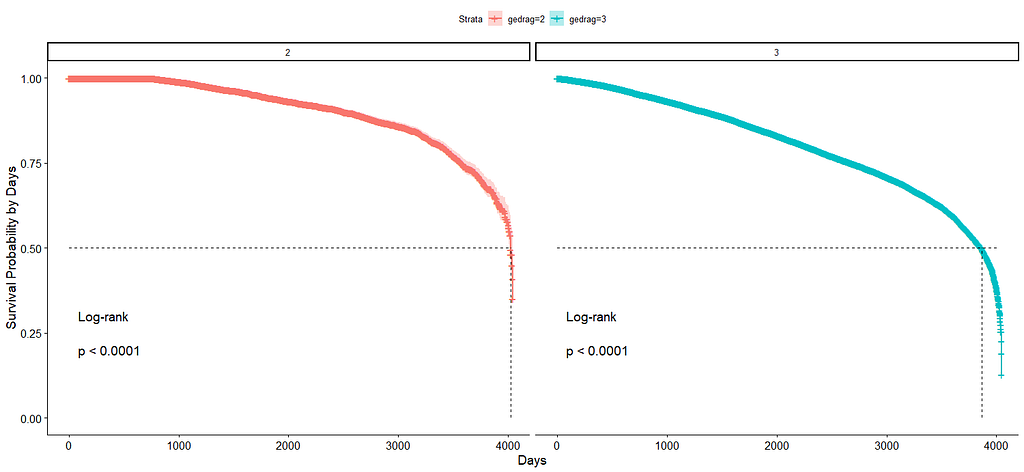
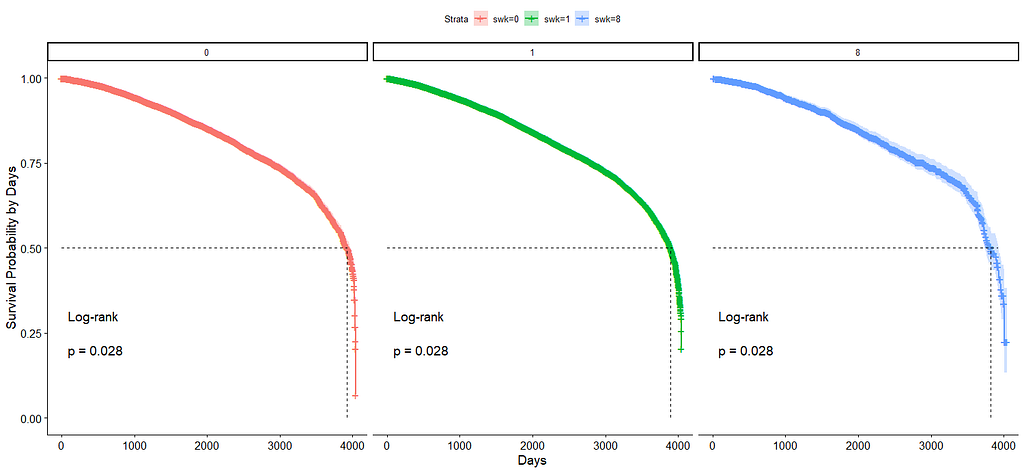
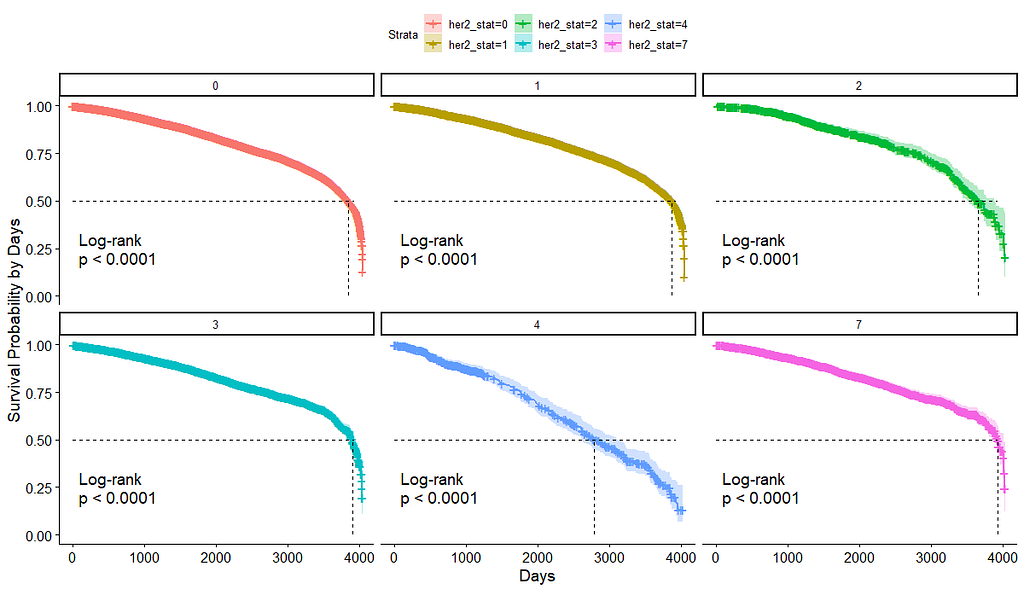
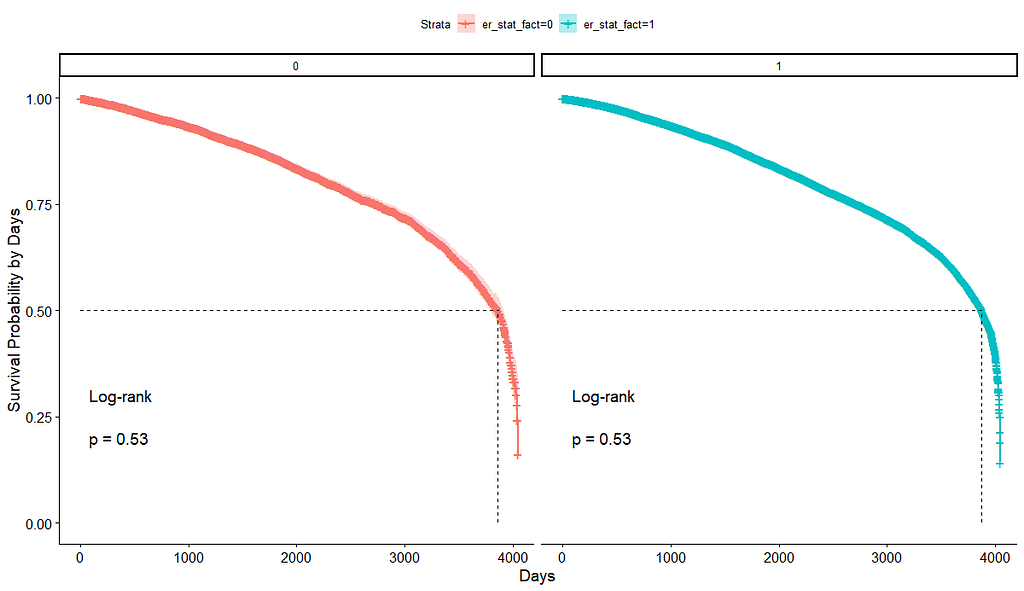
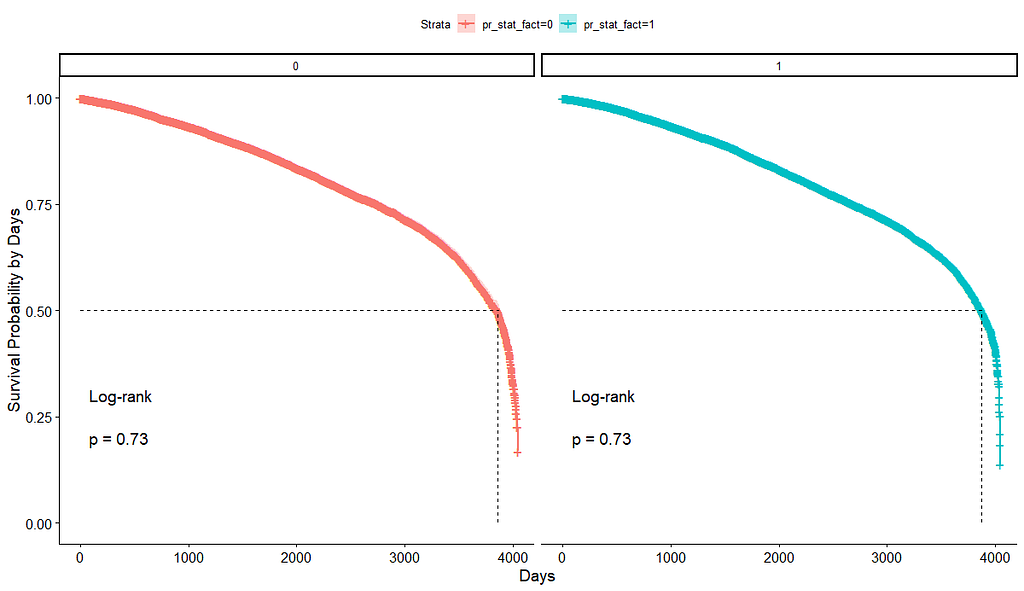
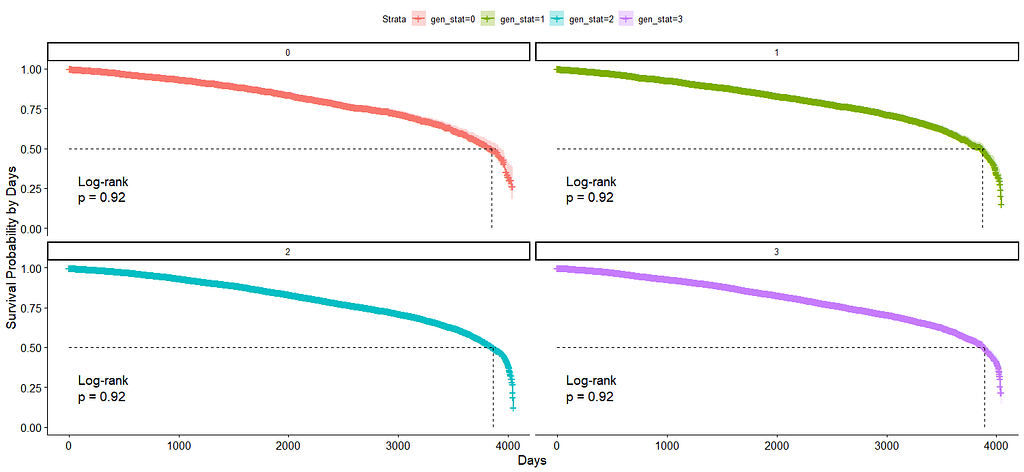
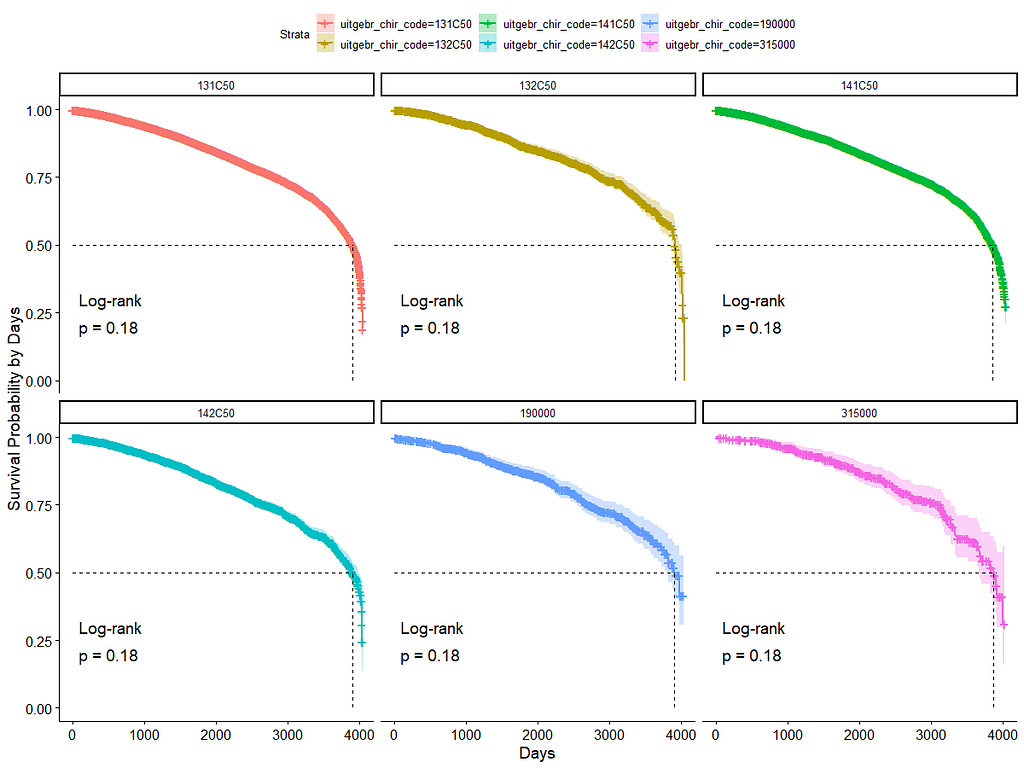
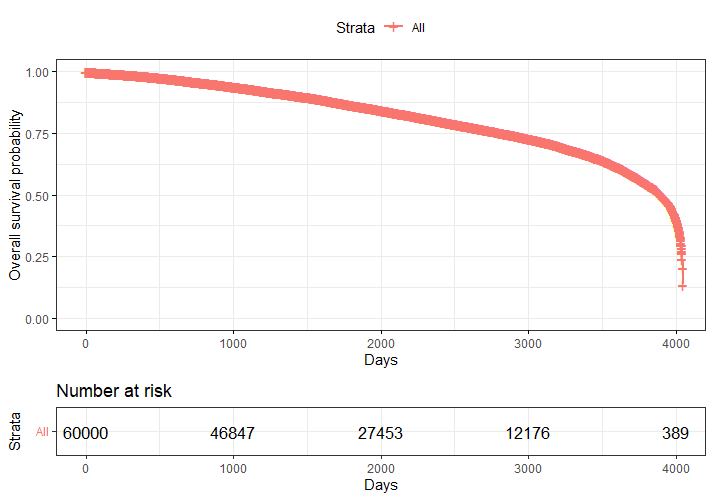
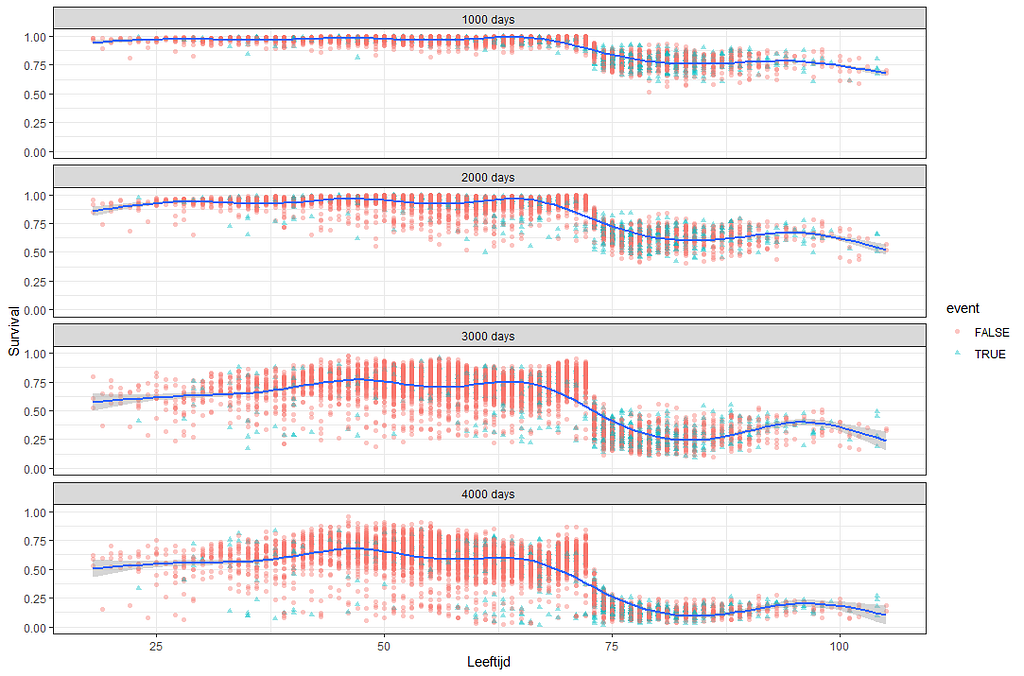
These plots clearly show that I cannot predict survival by a single categorical variable. Image: by author.

We have a lot of data to spend, but not a lot of variables and only a few of them are continuous. Those that are continuous, let's have a look and see if we can find cut-points that would yield completely different survival curves. Or at least, bring curves that have something interesting to say. Do not that this entire process is statistical driven — normally, biology should drive hypotheses and a first effort should be made to verify them via the data. Alas, let's go for the statistical approach and start with age.

The cut-point is set at age 72. So, we have higher and lower than 72. Image: by author.

That is a seriously interesting cut-point. Funny enough, if you look at some of the earliest graphs you could already see that age around 70 yielded a steep slope in survival time. Image: by author.

Indeed, age 72 is very interesting. Image: by author.

And also here, age 72 is very interesting, but only in combination with certain co-predictors. Image: by author.

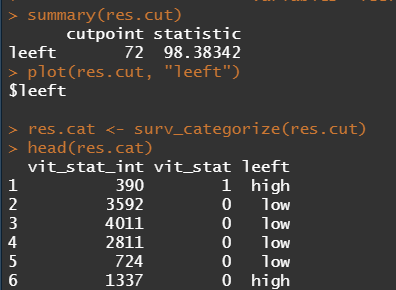
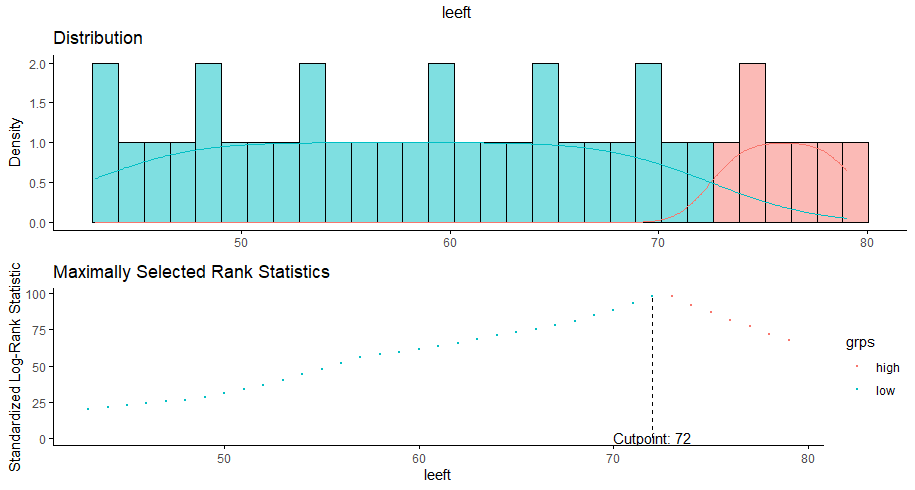
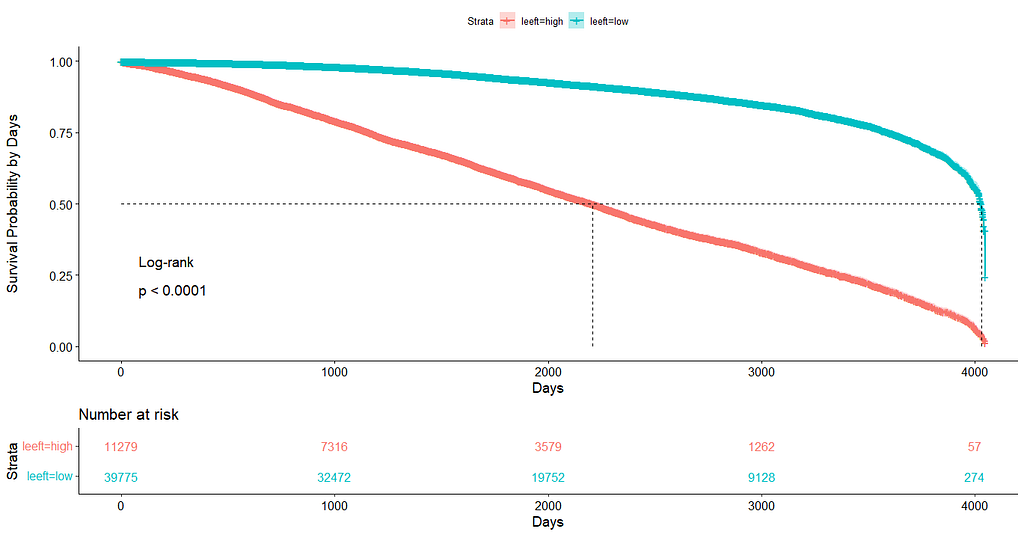
Now, let's create some survival curves, where we only look above age 72.

Now, the survival curves are starting to become much more interesting since they are the end of the bigger curve. This is where serious events are starting to take place. A difference in tumor placement can be found, but not hormonal indicators. Image: by author.

And, also differences between tumor size. Image: by author.

And now we see quite some differences. Image: by author.

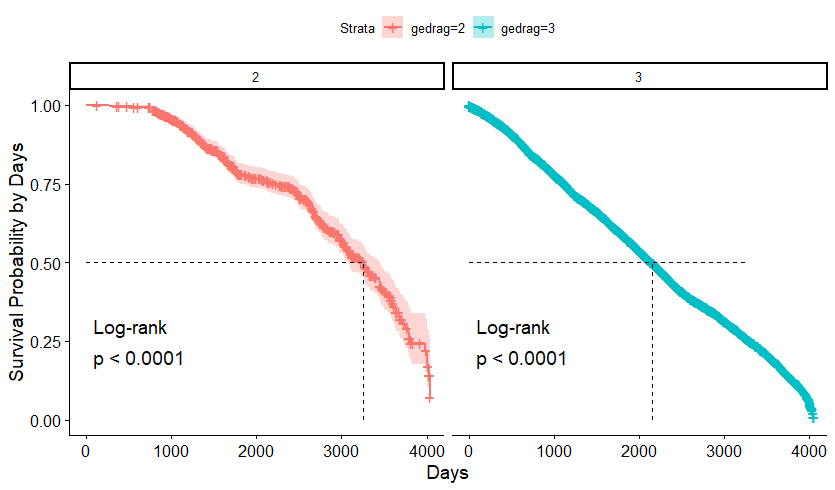
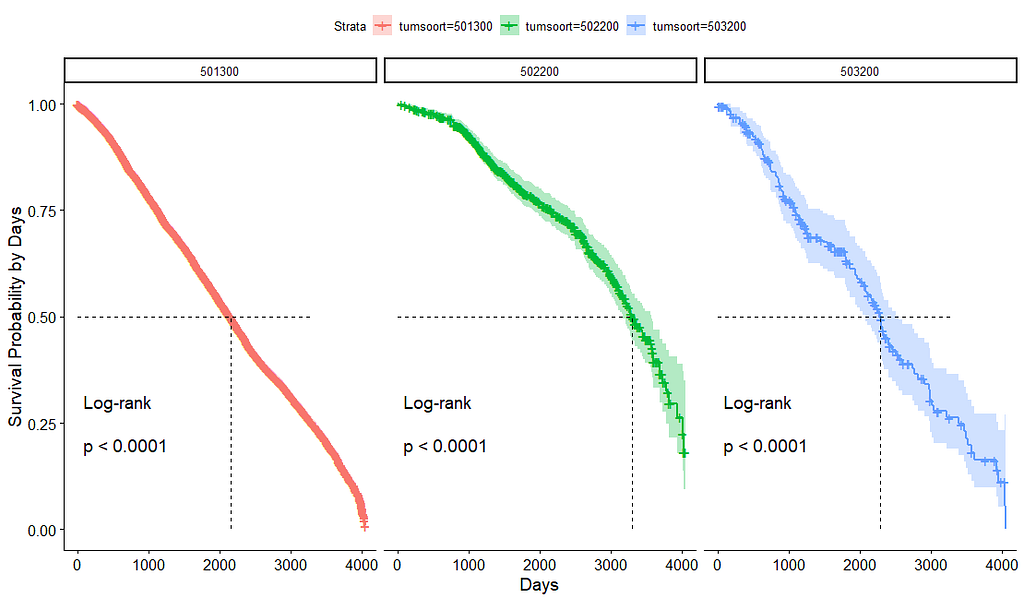
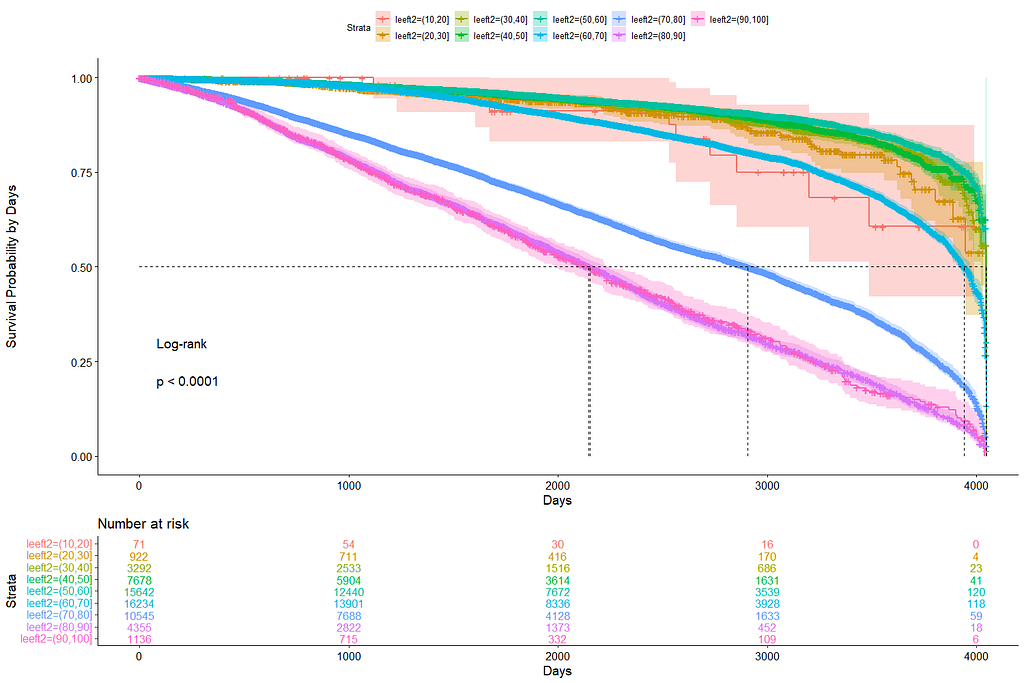
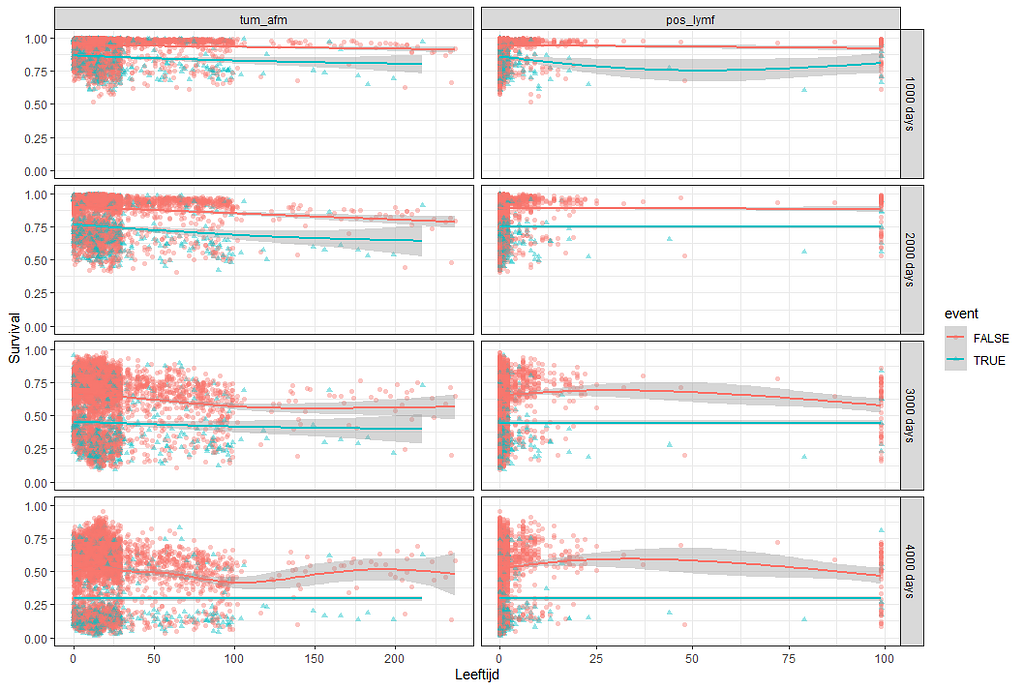
Good, we have something for age. Let's see if we can also find something for the number of positive lymph nodes. This one is not so easy, since there are mostly quite some lymph nodes examined, but the majority is not positive.

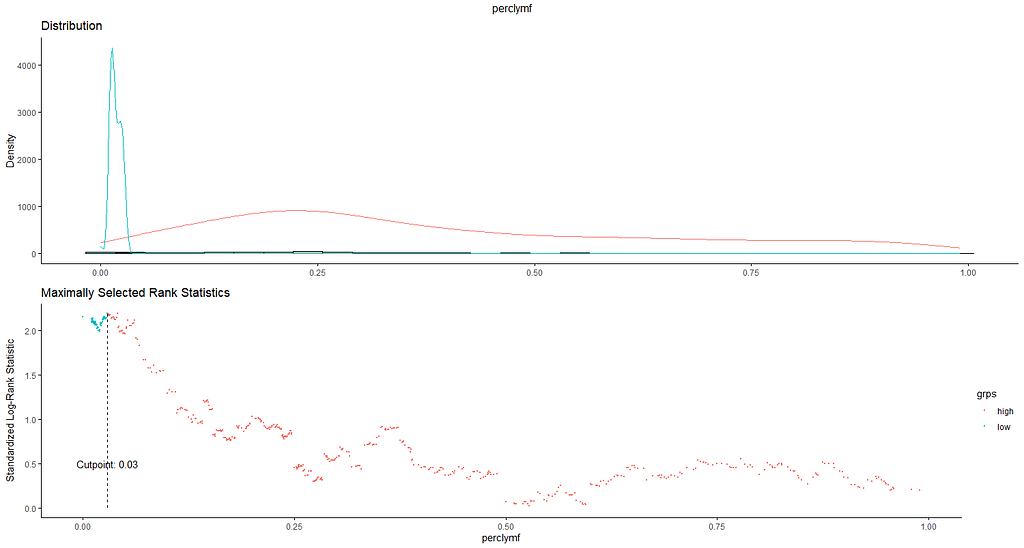
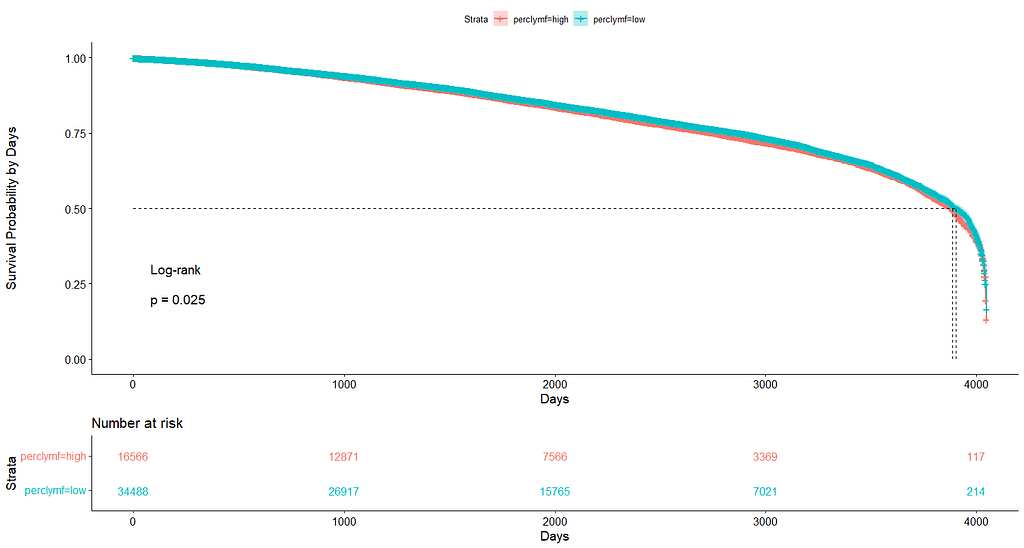
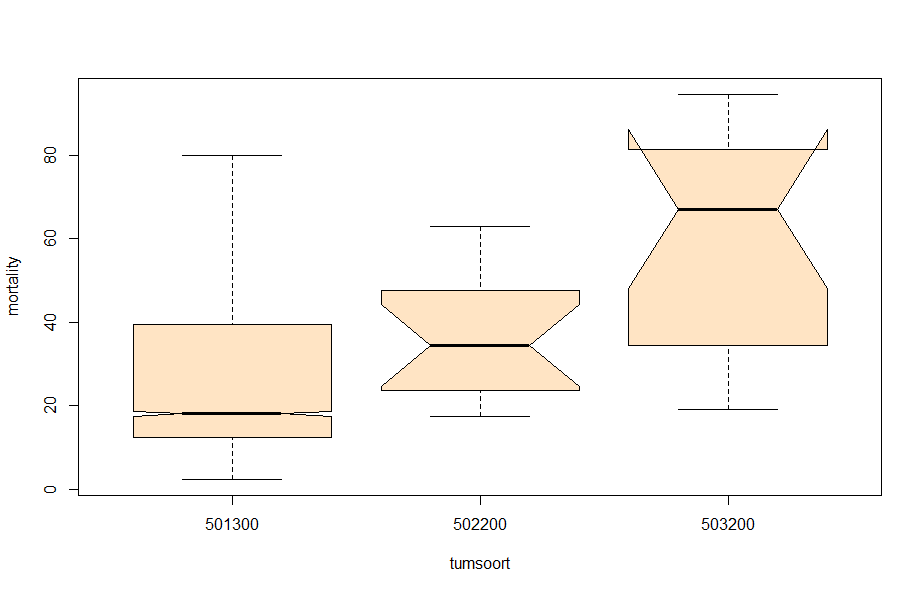
As you can see, a difference is found, can be found, but is found very very early. I wonder how this will hold up later in the model. Image: by author.

And, last but not least, tumor size.

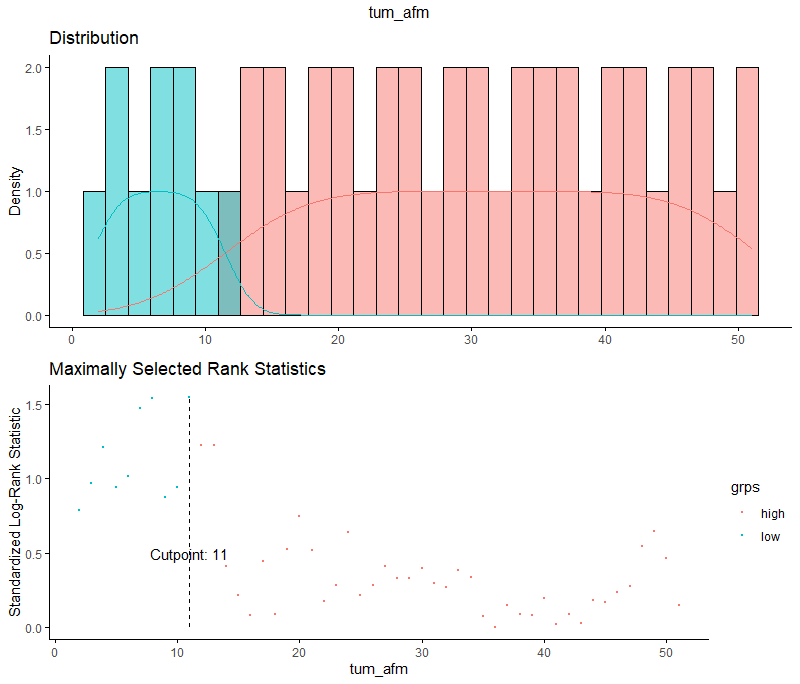
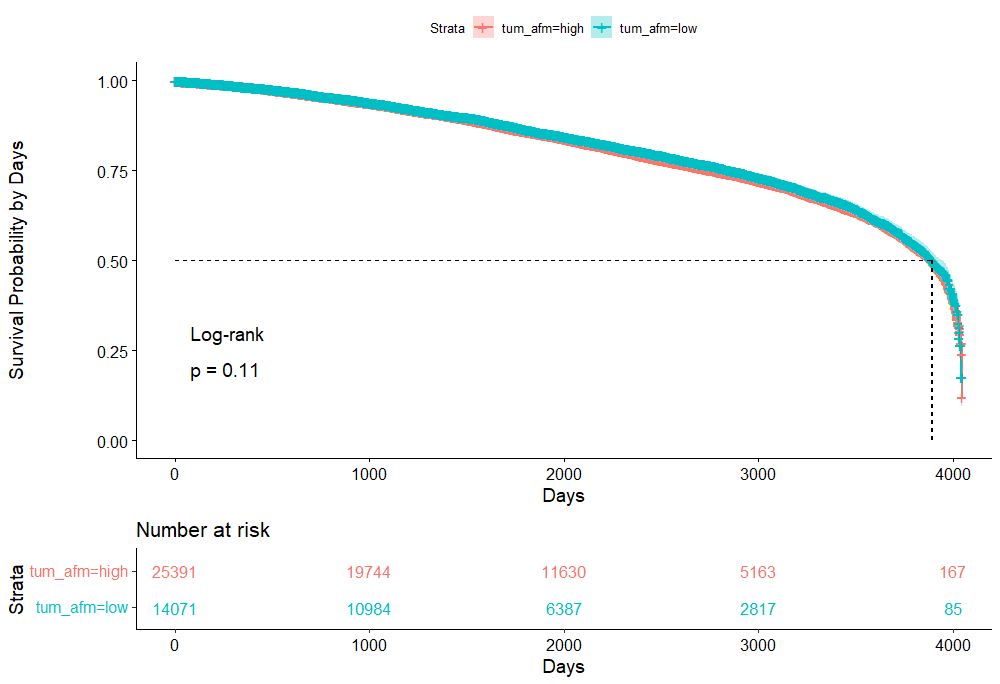
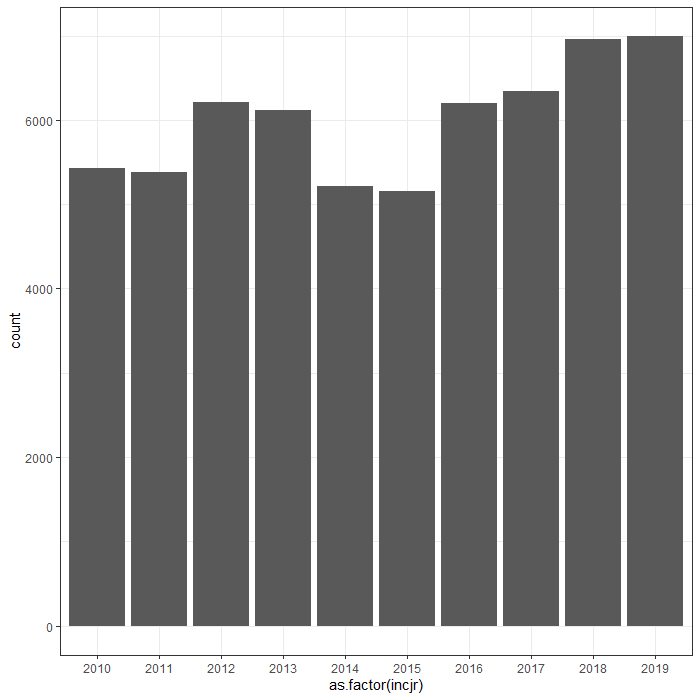
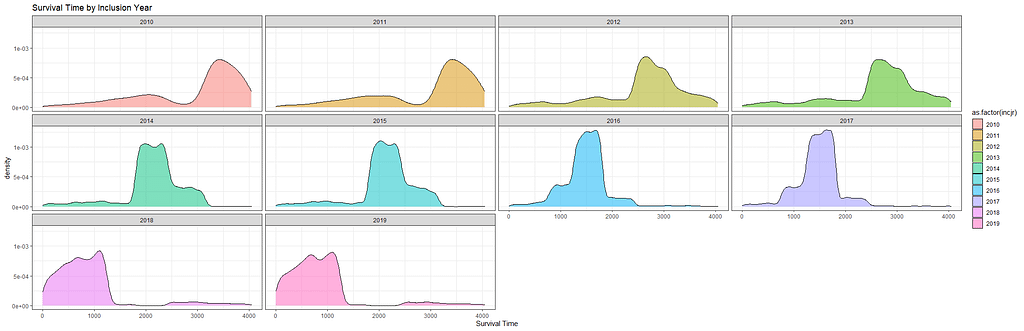
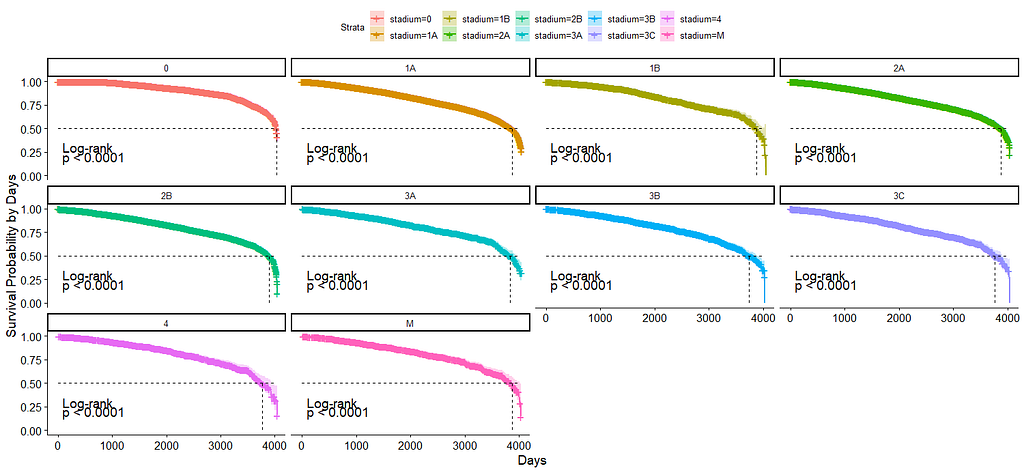
No significant result could be found, looking at tumor size alone, but biologically I would guess it does make sense. So lets see. Image: by author.

Then I could not resist looking at inclusion year. It makes no sense actually since it is a categorical factor, but let's take a look anyhow.

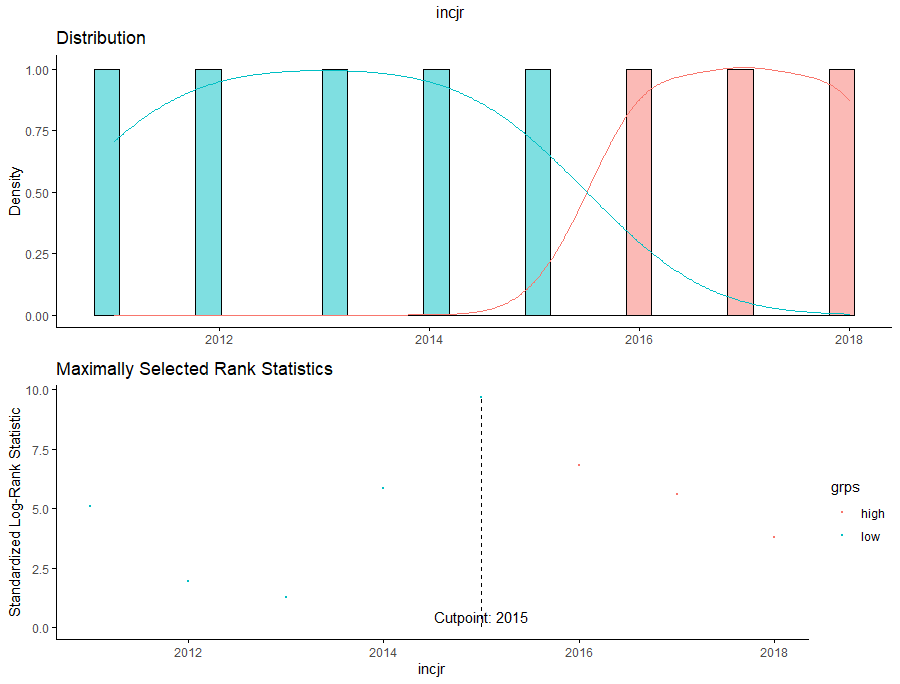
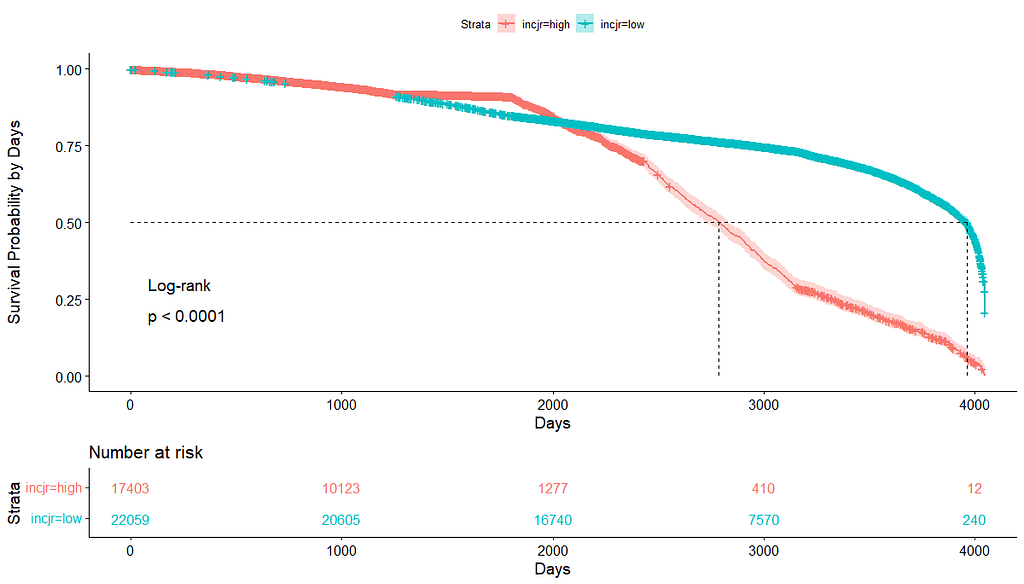
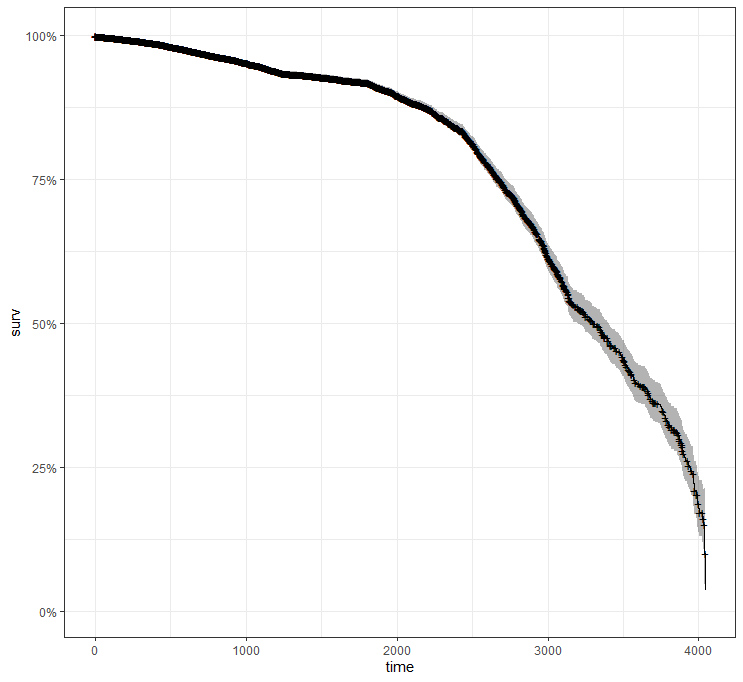
The cut-point is place at 2015. Which makes sense — they just did not build up the necessary survival time yet and censored data is not counted the same way as event data. Image: by author.

Okay, so I did some exploratory univariate survival curves. Let's advance and conduct a Cox Regression combining multiple variables.

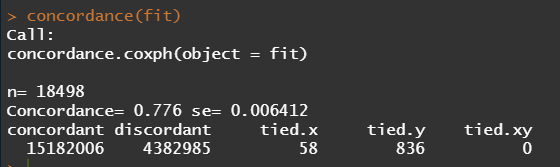
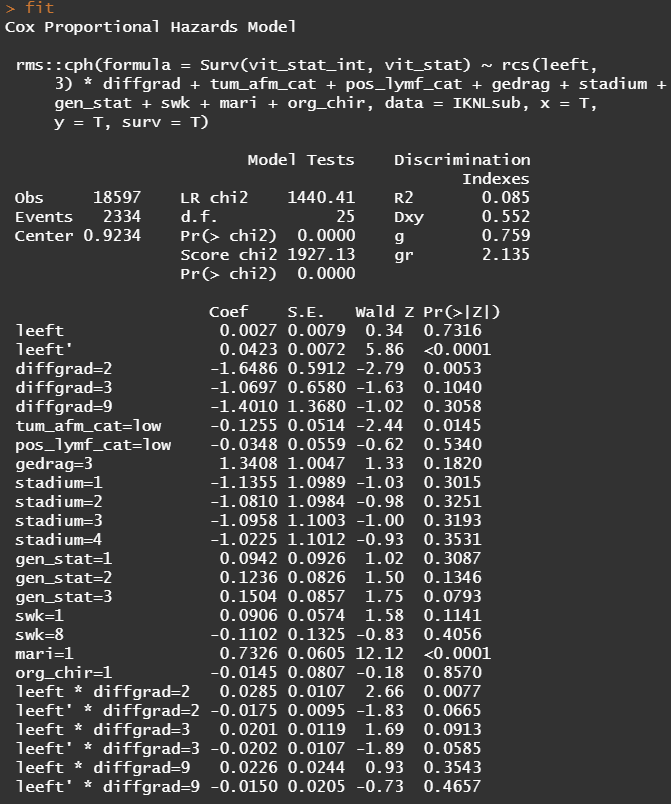
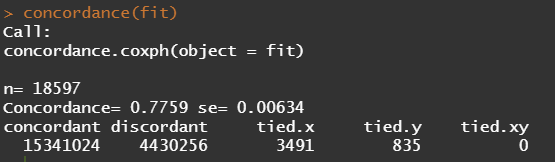
As you can see, the total fraction of events is around 25%. This should provide us with enough power to find a signal if it exists. Image: by author.

Below is the code for the cos-regression containing splines, looking for the predictive power (concordance), and showing the influence of each of the variables included.

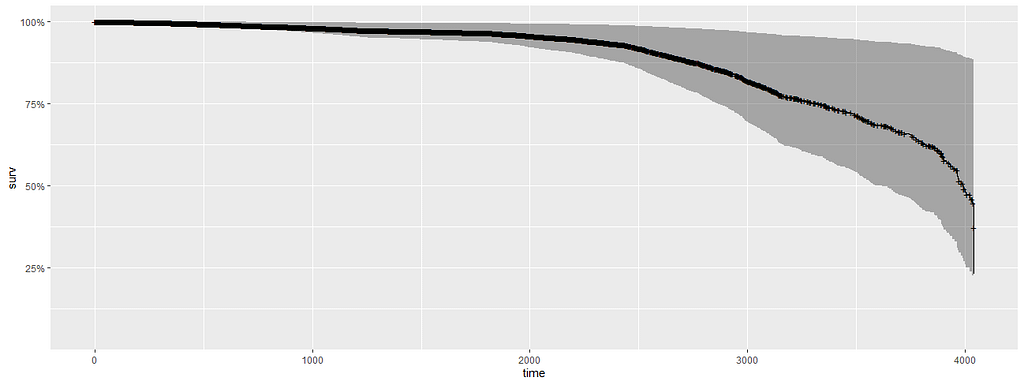
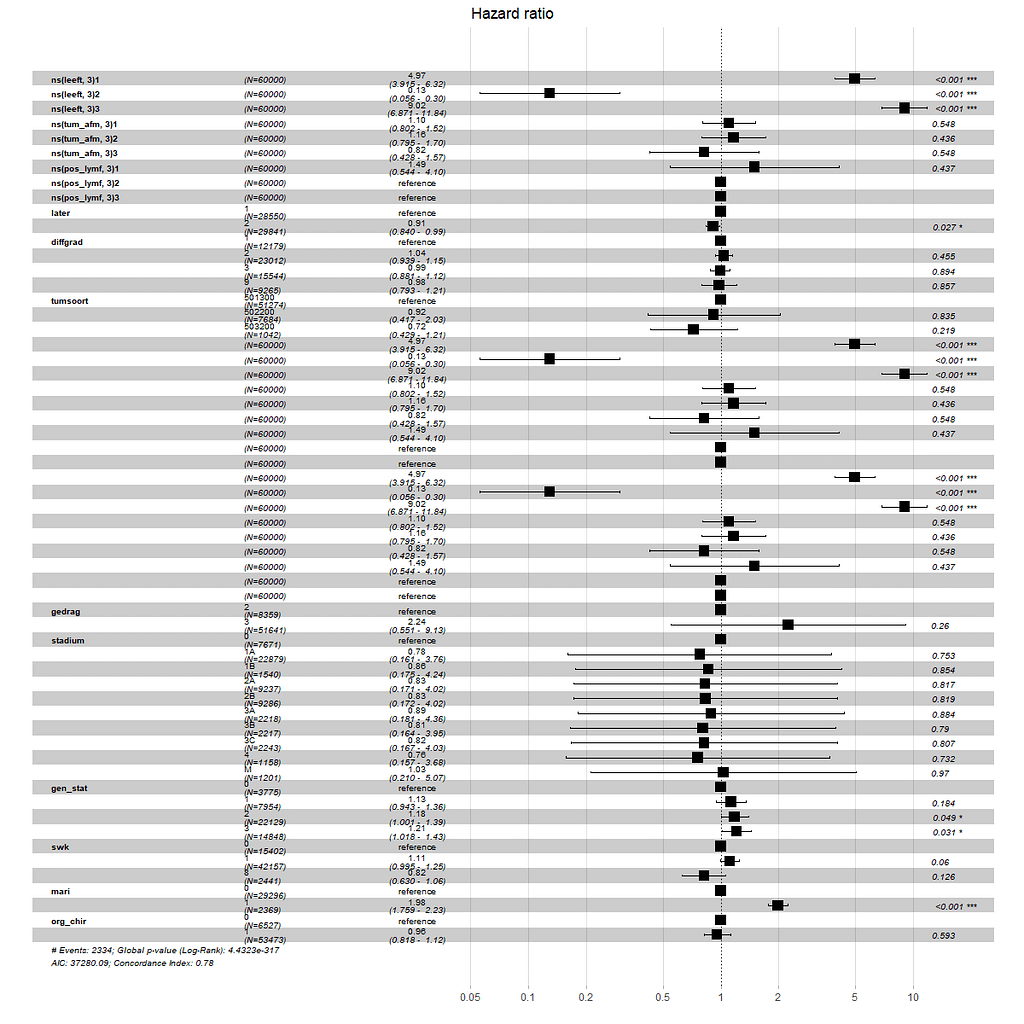
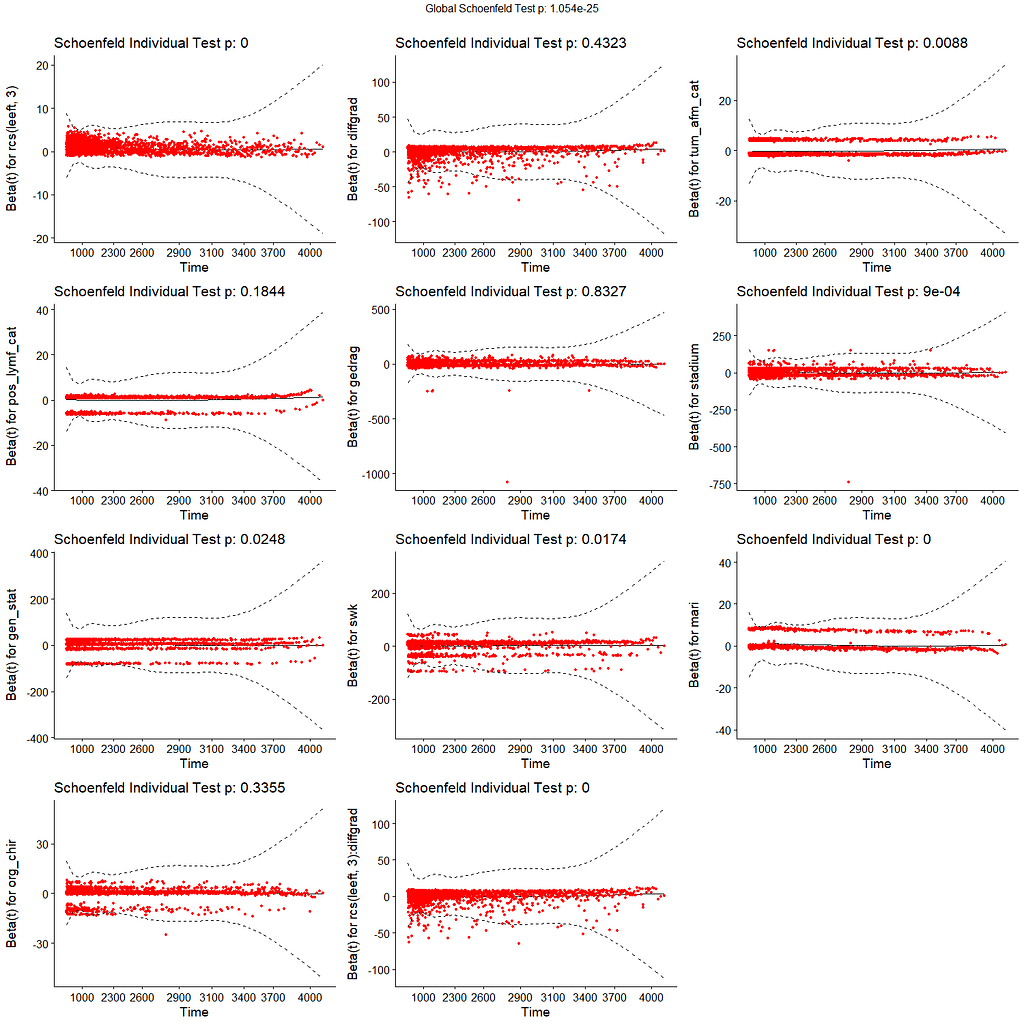
The c-statistic is set at 0.77 which equals the ROC curve in survival analysis. Image: by author.

And an impressive-looking Hazard Ratio plot. Not at all useful for communication, but it looks nice anyhow. Image: by author.

All of the above is useless if we do not first check the assumptions of the semi-parametric Cox regression. This means that the Hazard Ratios should be proportional and stable over time. I will also check if the splines fit the data well.

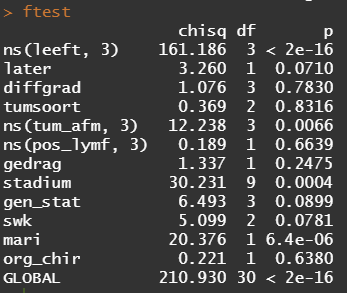
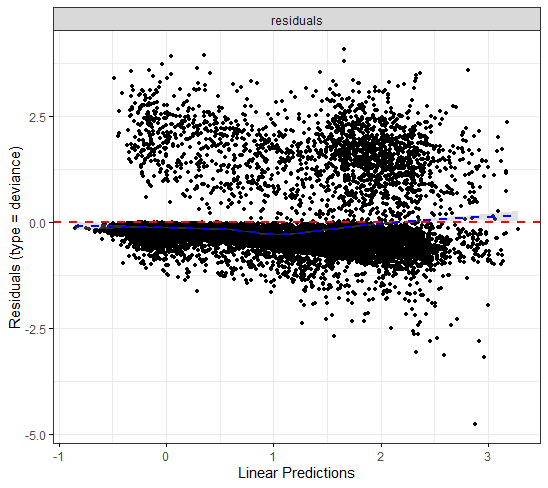
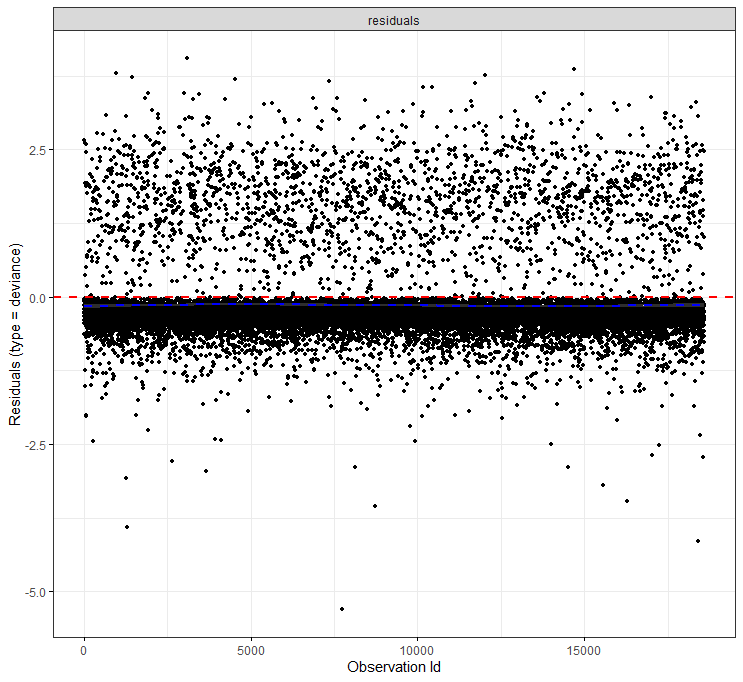
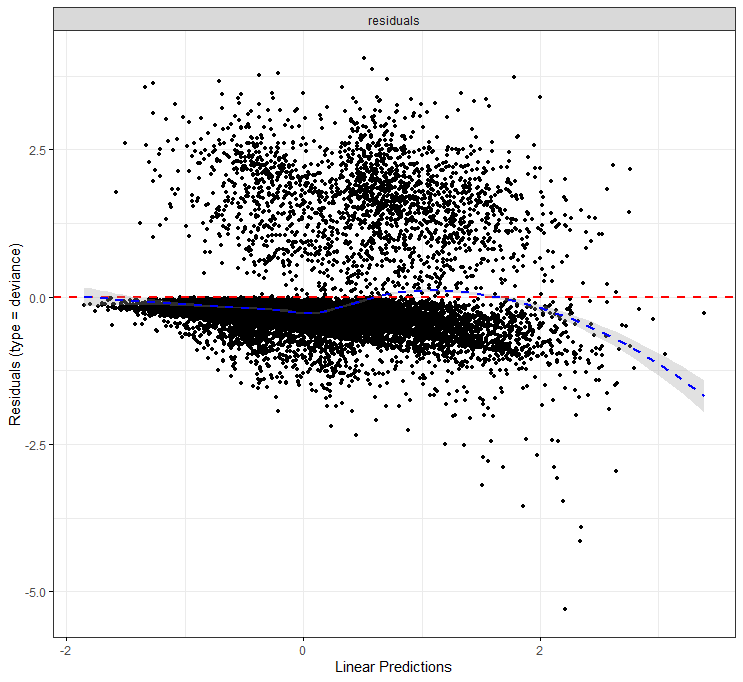
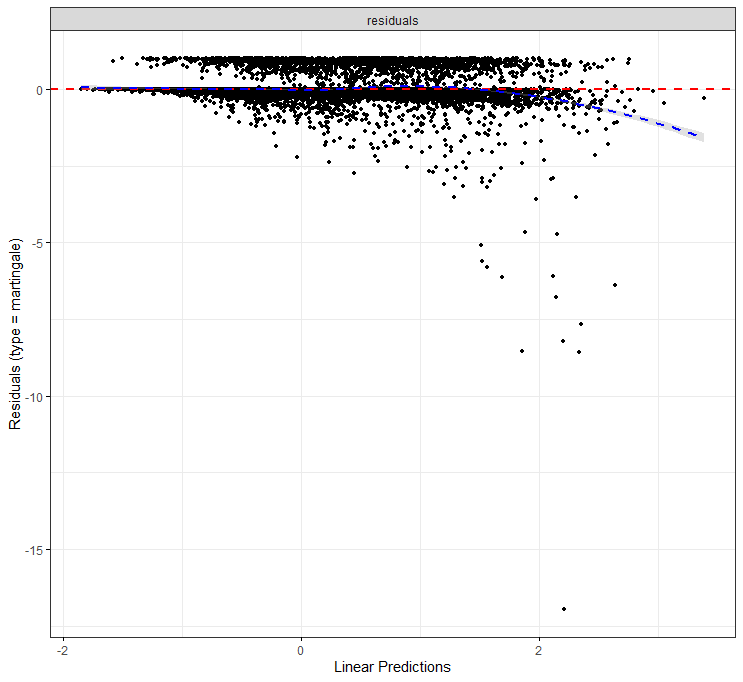
P-values are nice to use, but not really helpful. Significant means here that the proportionality assumption can not be kept. This is not good as it is the most important assumption of a Cox regression. If violated, the Hazard Ratio’s are not stable, and thus a function of time. Image: by author.

That we do not have plots for the Schoenfeld residuals, which test the PH assumption, is worrying. Image: by author.

The deviance residuals are the standardized residuals in a Cox regression. You want them to be homogenous.

This looks good, but also strange. Especially to the left. Image: by author.

I wanted to dig a bit deeper into the suitability of the splines. There is a function for that, but it does not accept splines. So, just have a glimpse, let's take a look by using cubic polynomials.

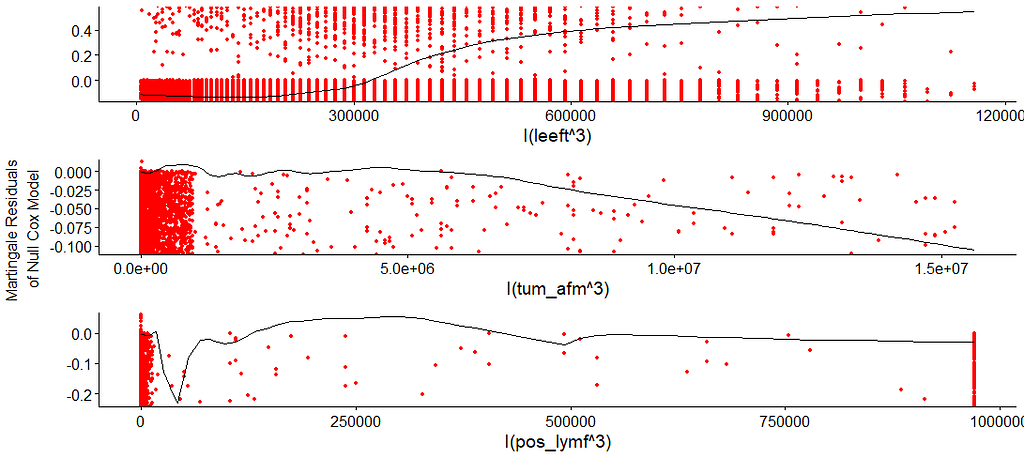
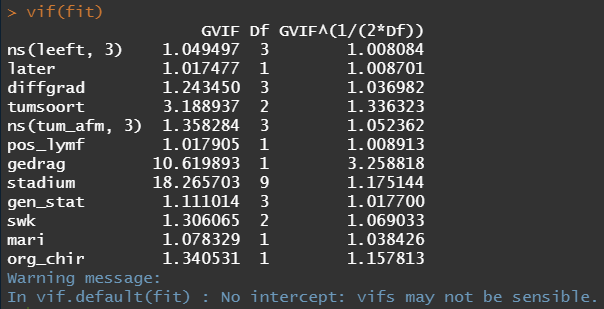
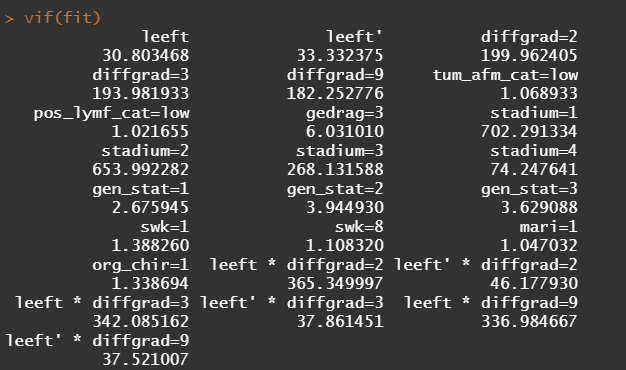
For all three, the martingale residuals are NOT linear. If I look at this, I am starting to believe that categorizing continuous data is not such a bad thing, even if it means that I may loose some predictive power. We already saw that the cut-points offer some explanation, although not for all. Image: by author.

So, in the next model, I deleted the spline for the number of positive lymph nodes. The variables probably need a transformation, but let's see how the model performs now, by looking at the Variance Inflation Factor (VIF). The VIF provides an indicator of the cross-correlations of the variables.

Lets take a look at the variance inflation factor. One variable stick out in particular, which is **gedrag** which means the tumor location. We need to look closer at that. Image: by author.

And now we have plots for the Schoenfeld residuals. They look good! I do not want to go for p-values, because with 60k observations, even the slightest deviations will be seen as statistically significant. Image: by author.

And the residuals and linearity assumption. I can live with these plots. Image: by author.

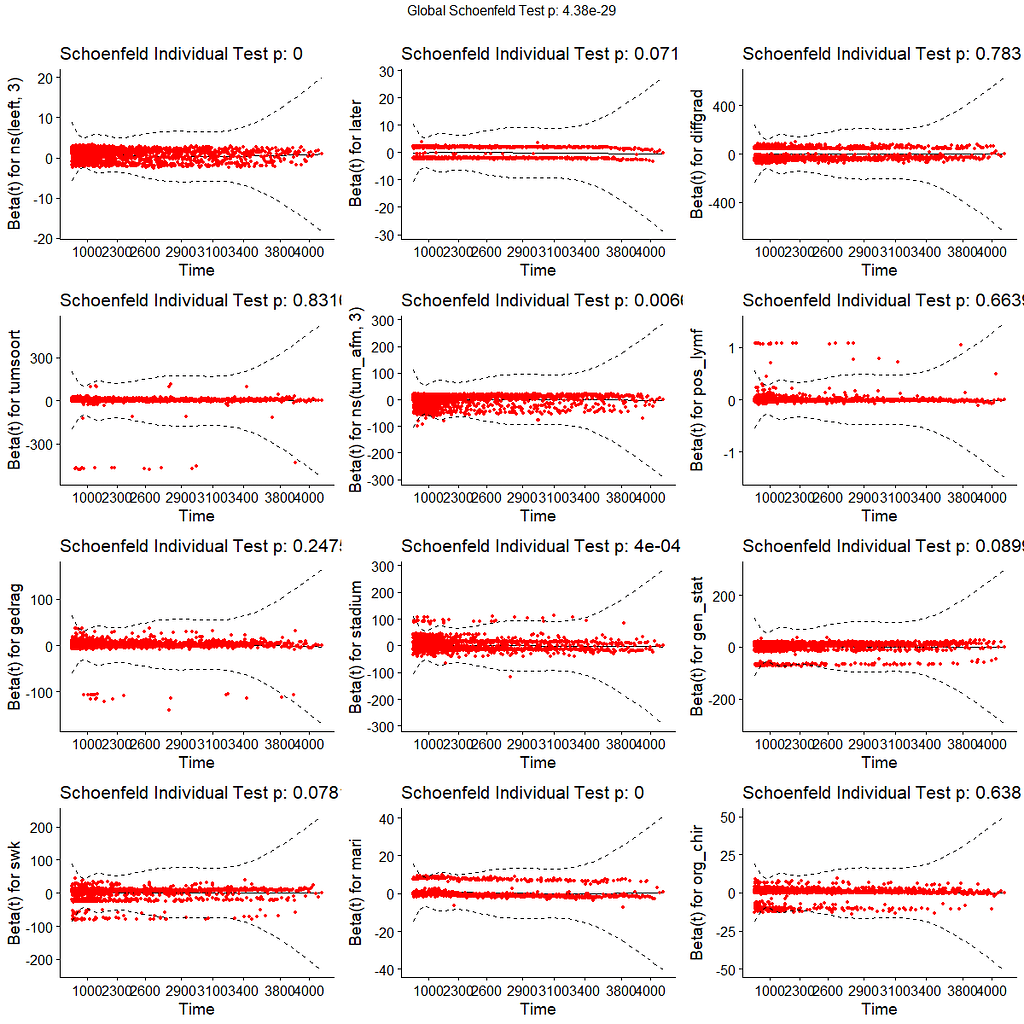
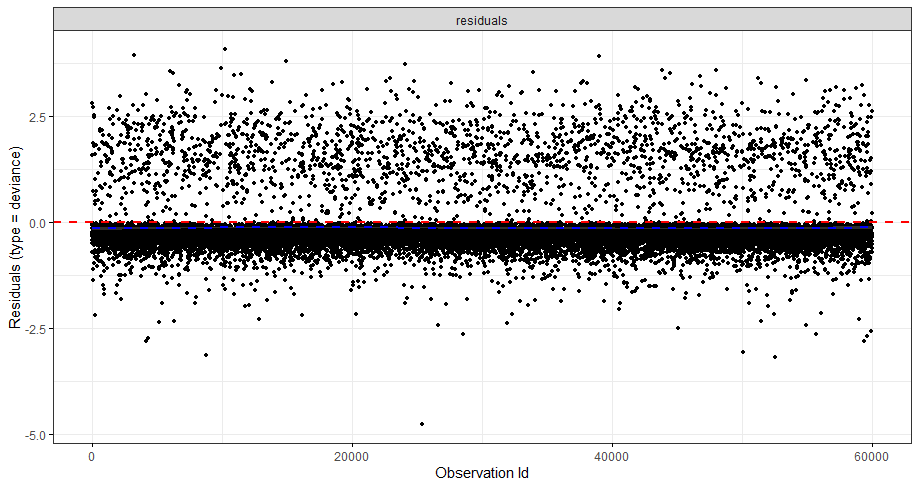
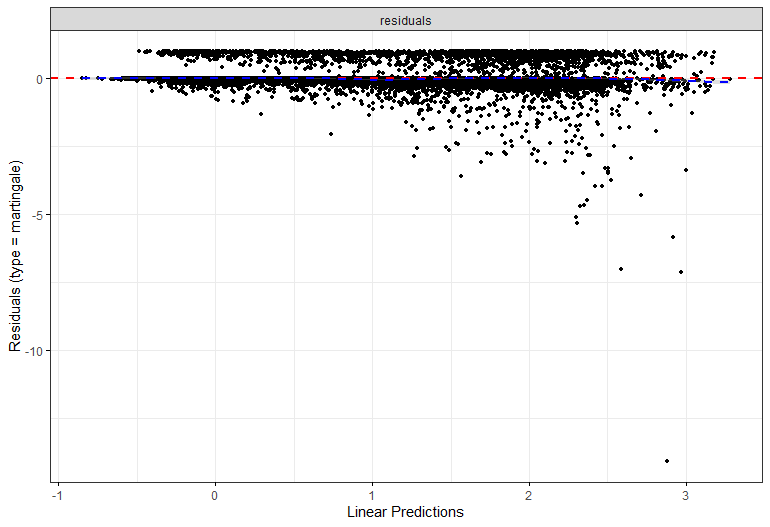
A sensible next step would be to assess the predictive power of the model. Well, actually, I want to see if the model can discriminate between groups, so I made three risk profiles (I am not even sure if they make biological sense) and see what the models predict.

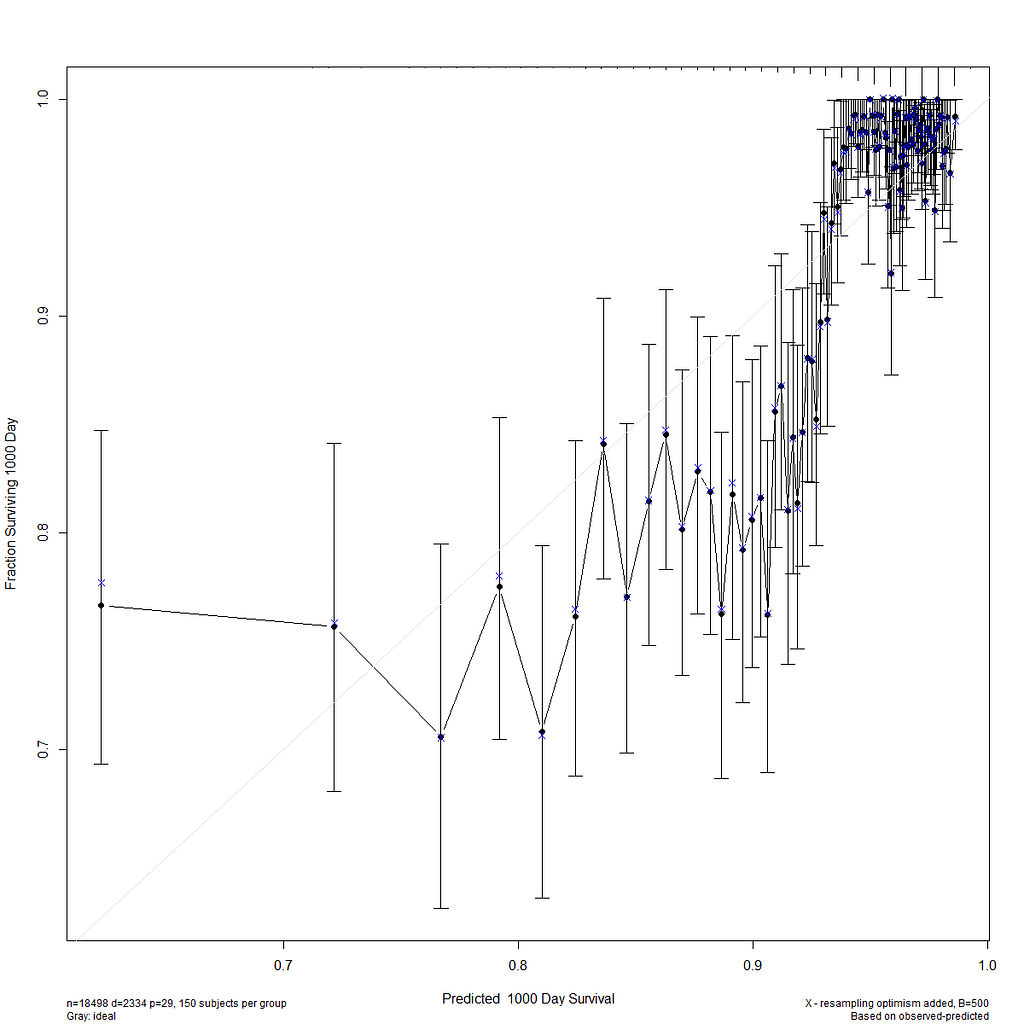
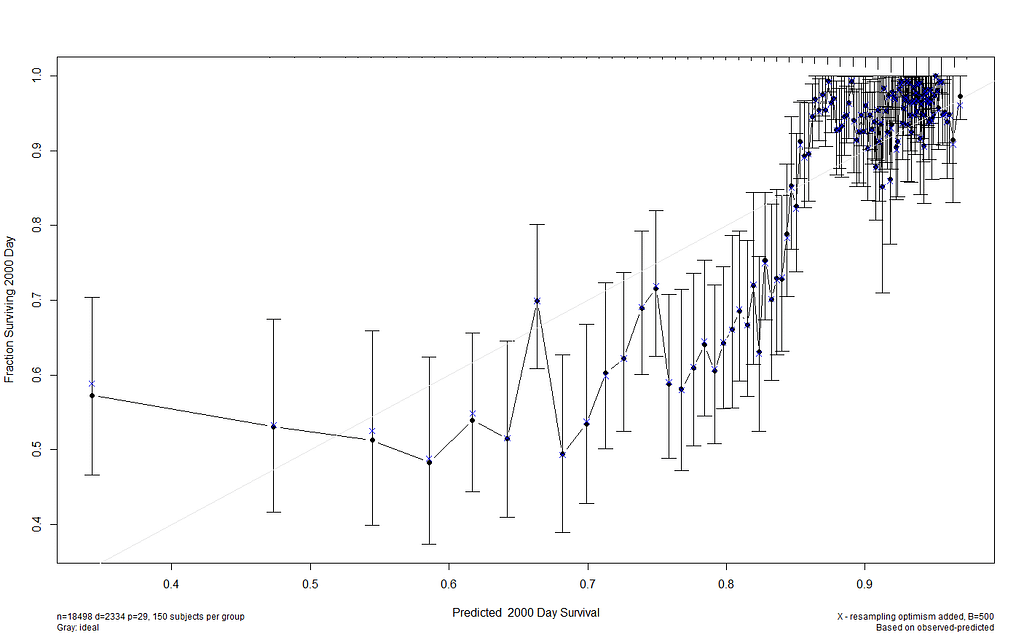
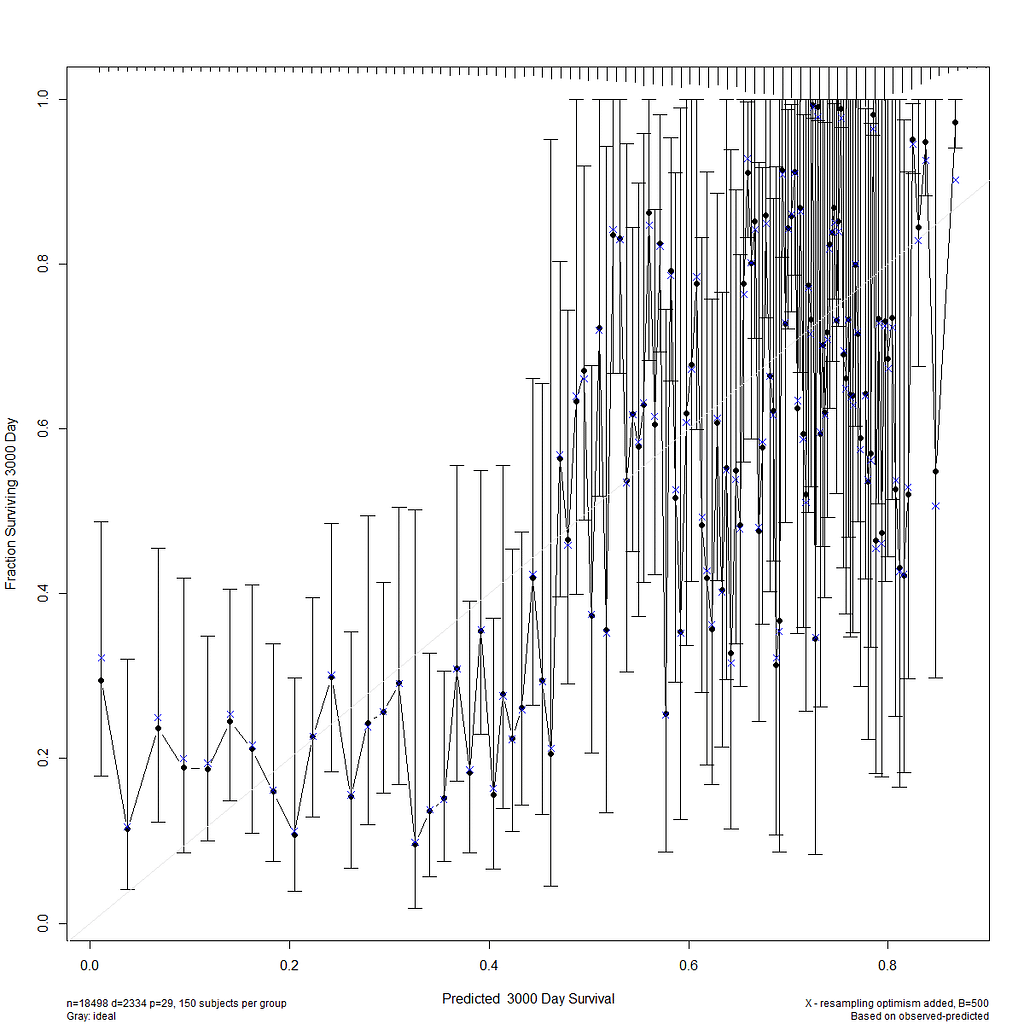
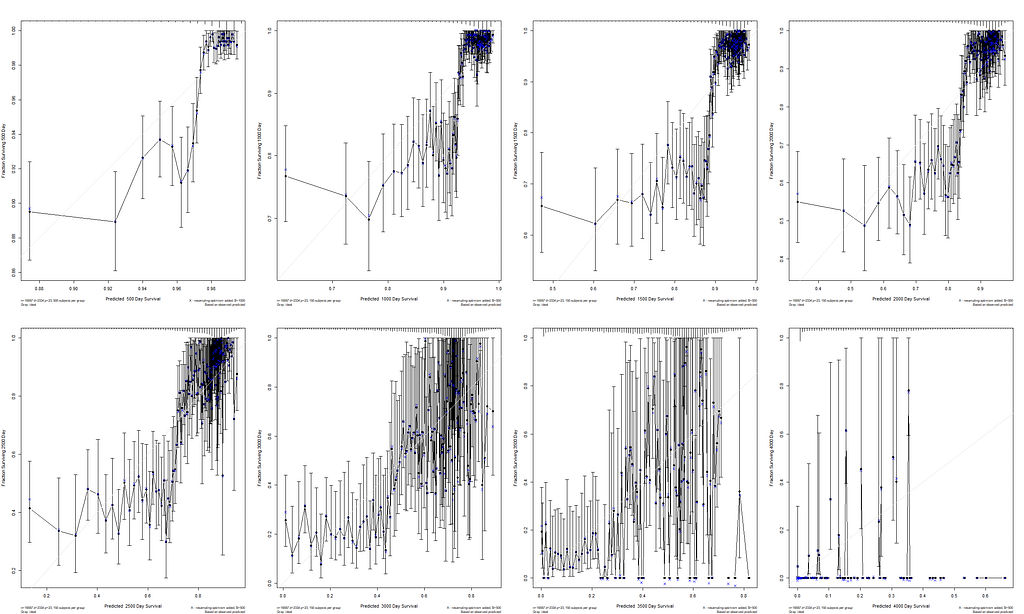
I am not sure if the risk profiles make sense, but they are for sure discriminating. Image: by author.

I already showed that to assess a model, you can look at the residuals and the concordance statistic. In the rms package, there are also some great tools to validate your model via bootstrapping. At particular time points. Let's see how this turns out.

The bootstrapped calibration plots for 1000, 2000, and 3000 days. Not that great, also not extremely bad, but we can do better for sure. Image: by author.

In this day and age of machine learning, we can go and try for some additional models. The first is actually an old, the Nelson-Aalen estimation which is the non-parametric brother of the Cox regression which is semi-parametric. The Nelson-Aalen focuses exclusively on the hazard function and will provide us with plots to show the influence of each predictor on the hazard function. Quite important information.

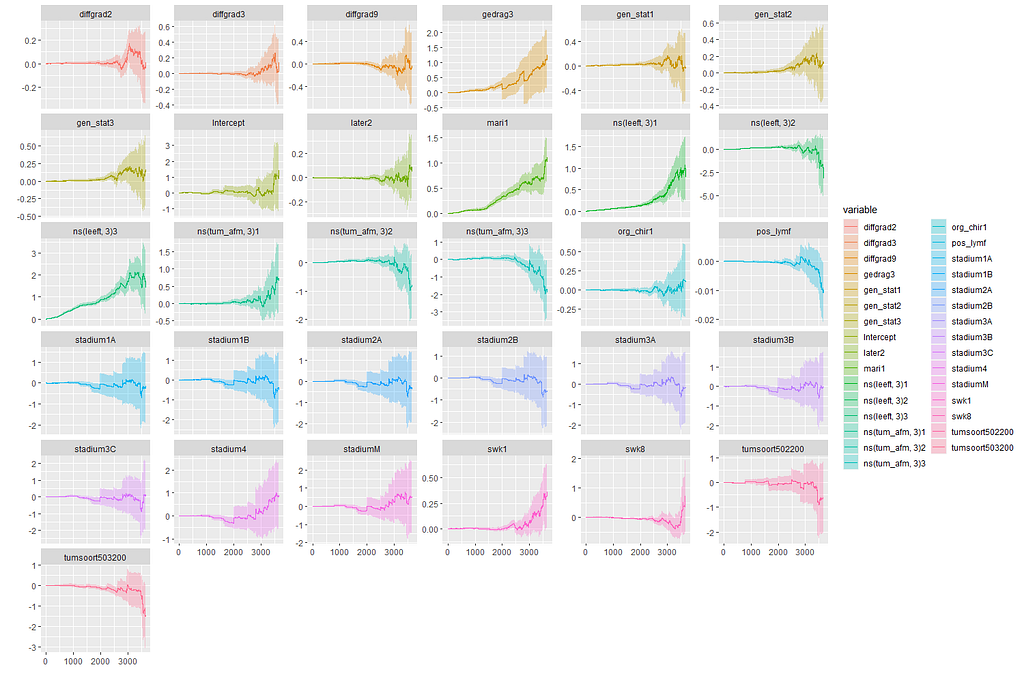
And here, the influence of each predictor on the hazard. What you are looking for is a trend. That the confidence interval increases at the end is normal due to the number of censoring going on. As you can see, some of them seem to have little influence, but others definitely do. Image: by author.

Next up, is true machine learning. The Random Forest. To me, this is just a tool to look at which variables were deemed important, not to use it to predict. The reason is that the Random Forest becomes very easily unexplainable.

On the first try, I used the ranger package.

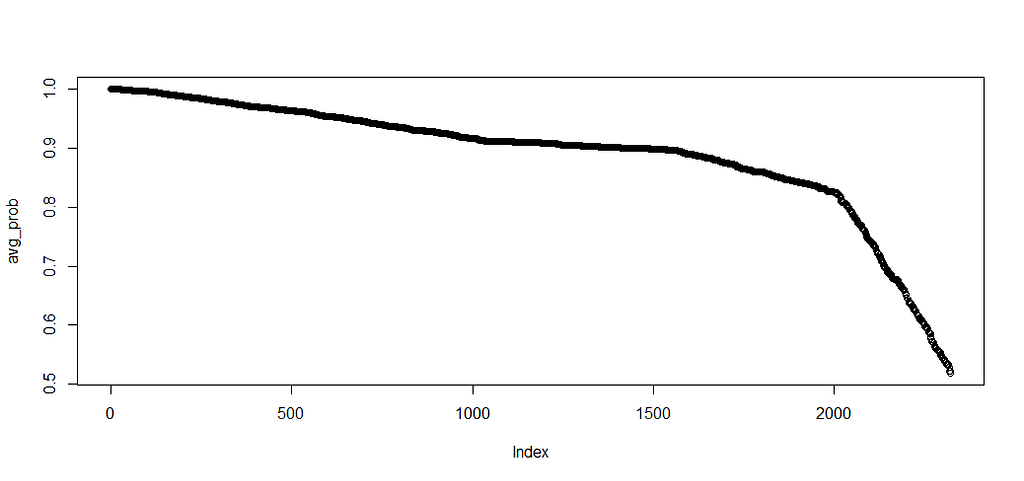
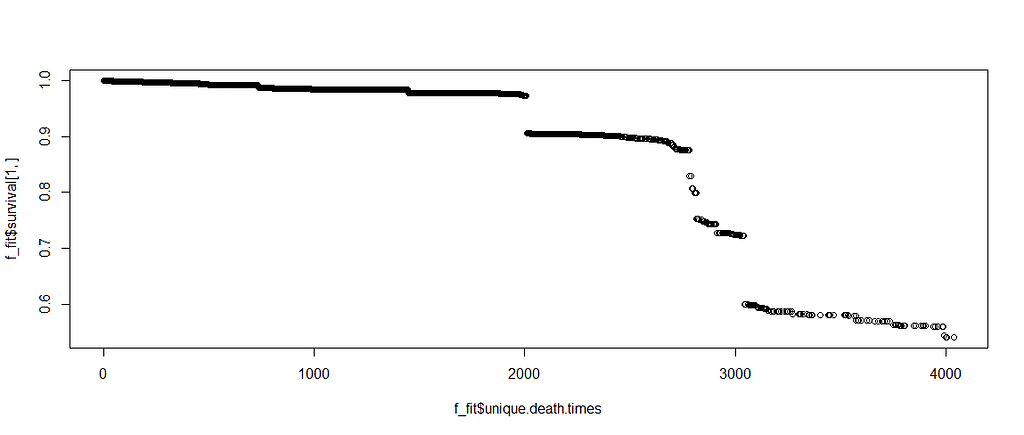
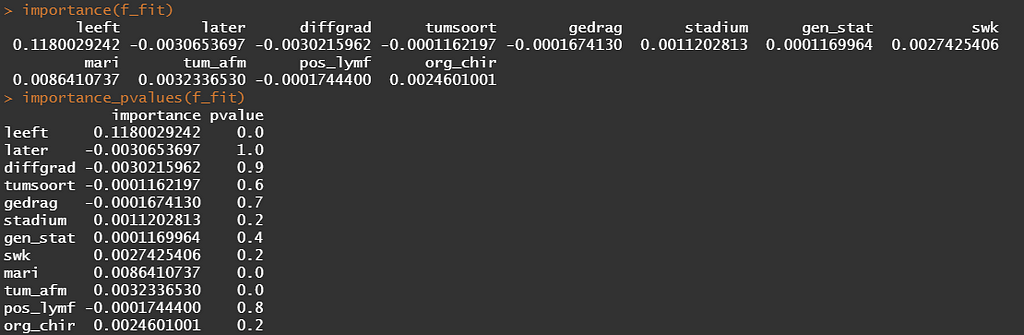
The survival curve to the left, and the predicted survival curve to the right. Image: by author.

The variable important metrics. As you can see, some are really important, whereas others are for sure not important. Based on the p-values, one could only include **age**, **mari**, and **tumor size**. Image: by author.

Let's try another package — randomforestSRC. In addition to running a Random Forest for time-to-event data it also provides nice ways to plot the data. The standard option will build 500 trees.

The most important metrics, by far. The number of trees in relationship to the error rate, and the variable importance plot. The random forest of this package agrees with the Random Forest of the previous **ranger** package. Image: by author.

The error rate plotted by **tumor kind**. Image: by author.

A single tree depicted from the Random Forest. Despite a tree being completely explainable, it becomes very unyielding if you look at it this way. Image: by author.

Predicted survival probabilities. Image: by author.

Partial Dependence Plot for **age** and **tumor kind.** Image: by author.

Graphs showing the minimal depth of the variables included. Minimal depth for a variable in a tree equals to the depth of the node which splits on that variable and is the closest to the root of the tree. If it is low then a lot of observations are divided into groups on the basis of this variable. You can see how the values above are related to the Variable importance plot. Image: by author.

Plots showing the relationship between variables and survival as seen by the Random Forest model. Image: by author.

The interactive minimal depth — the importance of the variables included in relation to the other variables included. Remember, the lower the better. Image: by author.

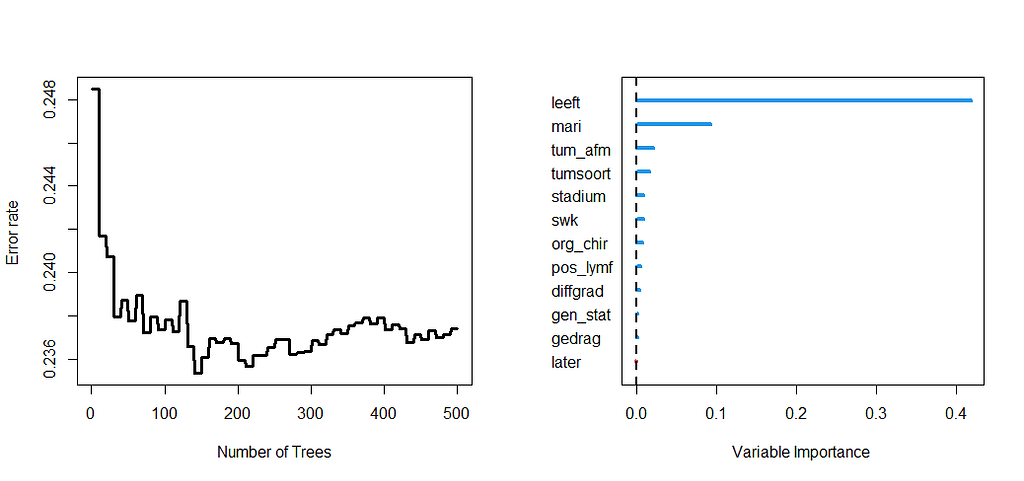
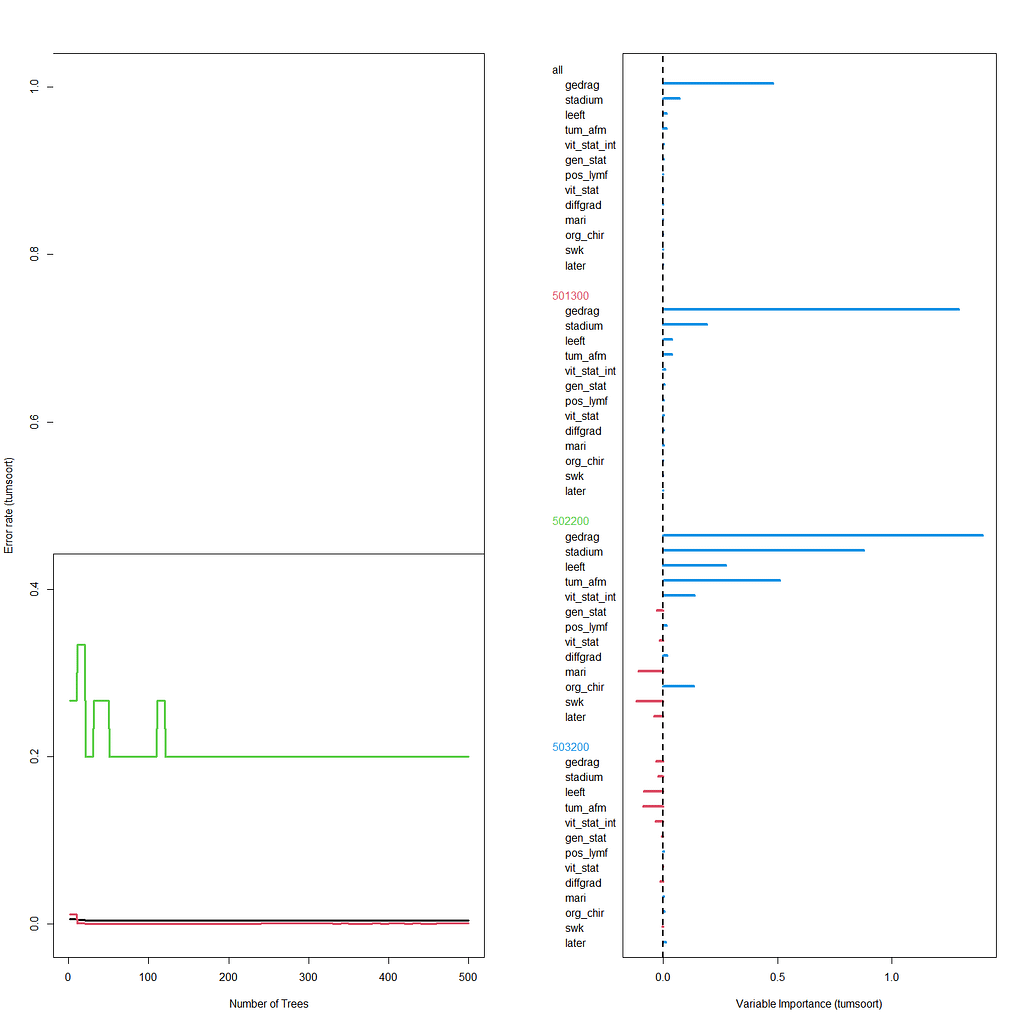
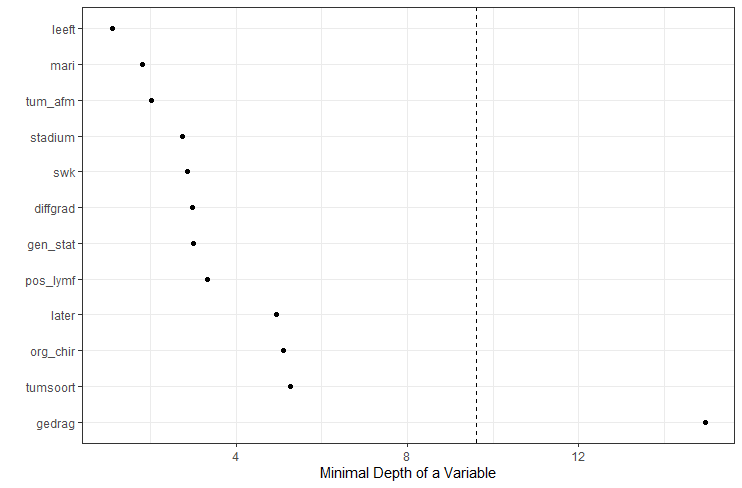
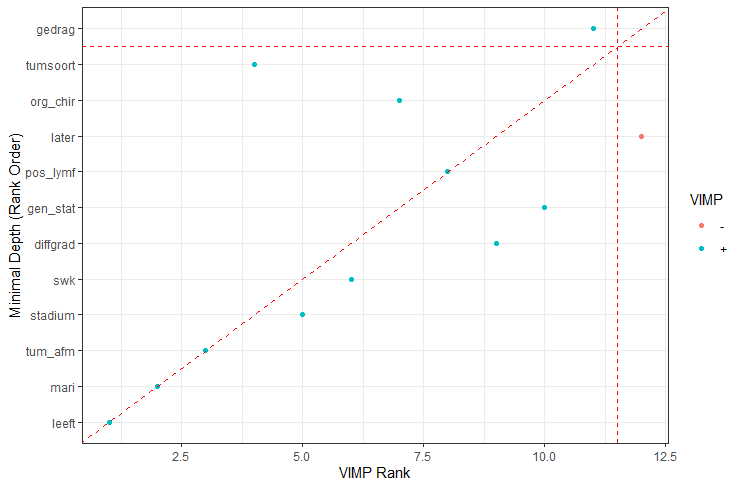
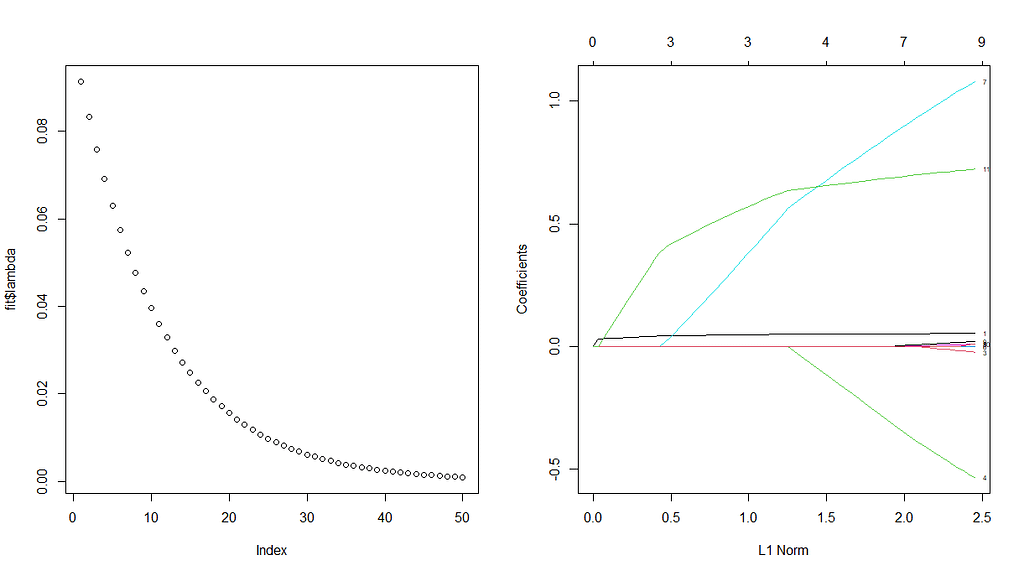
The random forest models above already clearly showed that some variables are not that interesting whereas others are. Now, one of the best methods to look at variables and their importance is to include the L1 and L2 penalization methods — LASSO and Ridge Regression. I posted about these and other variable selection methods before.

These methods were applied to a subset of the data since the entire dataset gave problems with memory size that I could not solve. As you can see I only subsampled once, but a better way would be to loop this dataset and do it many many times so you get bootstrapped estimates of their importance. For now, we keep it easy and make a subset of 10k.

First, we will ask the penalized package to profile the L1 and L2 parameters and then search for their optimum. Once we have that, we apply them both. By applying them both, we deploy what is called an elastic net.

Here you can see L1 and L2 working via their plot paths. The difference between them is that L1 will delete variables by shrinking their coefficient to zero, where L2 wil adjust them. The L1 takes a lot of time to come into play and in the end selects only a handful. Image: by author.

Optimal L1 variable selection via shrinkage. Image: by author.

Optimal L2 coefficients. Image: by author.

The coefficients of the Elastic Net. As you can see, some categories of factor variables have been abolished completely. This is for instance the case for tumor stage (**stadium**) and hormonal receptors (**gen_stat**). Image: by author.

The prediction models based on the elastic net. Image: by author.

The predicted survival curves for the 10k included patients. The shape seems to be about right but then again, the plot really does not help when you have so many IDs included. Image: by author.

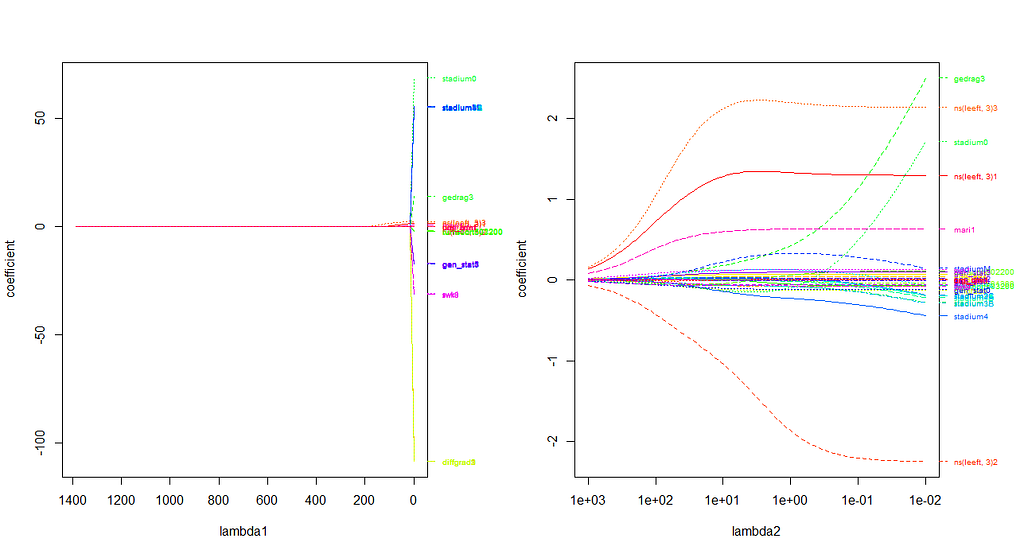
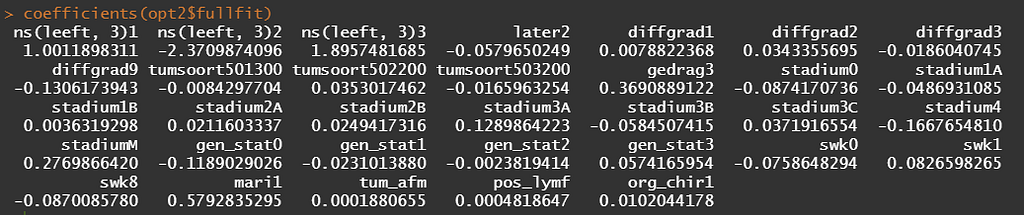
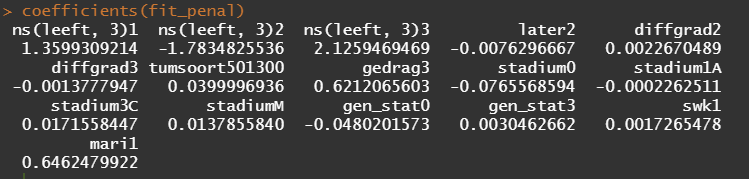
Besides the penalized package there is also the GLMNET package. Lets give this one a try as well.

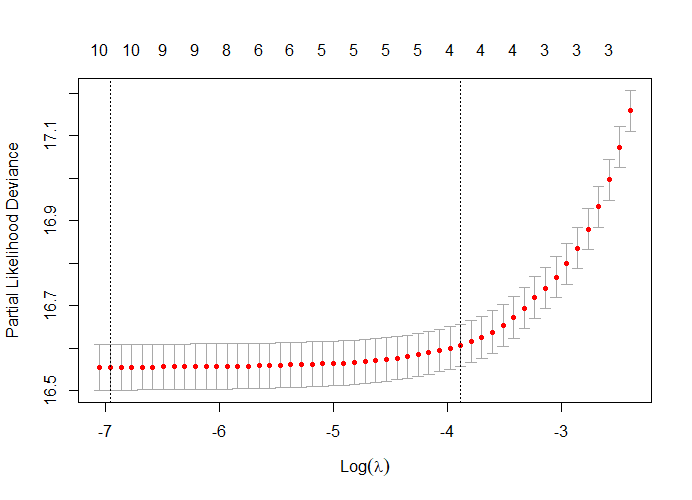
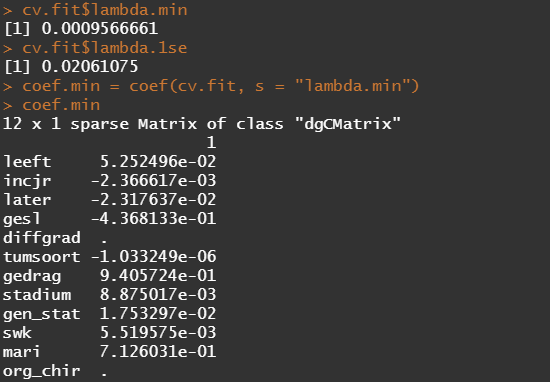
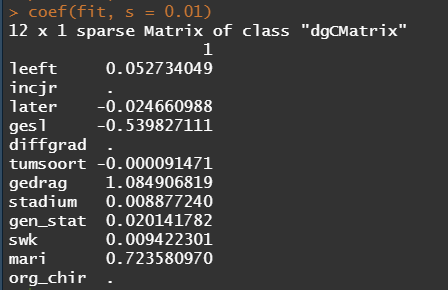
L1 via a normal procedure, and looking for the optimal lamba via cross-validation. Image: by author.

Applying the cross-validated lambda value and see how inclusion year (**incjr**), differential grade (**diffgrad**), and surgery (**org_chir**) are deleted from the model. Image: by author.

The following part is a bit experimental for this particular dataset since I do not really need it. Below you will see me fit parametric survival models, which try to bring survival curves to the end by modeling beyond the data. Now, modeling beyond the data via a (statistical) model is always tricky, but this kind of model ARE accepted and often used in Health Technology Assessment procedures.

The survreg procedure automatically fits the Weibull model if nothing additional is specified. Image: by author.

The fit of the model, based on the time-to-event data (**vit_stat_int**), tumor kind, tumor stage (**stadium**), and age (**leeft**). Not really a good fit. Image: by author.

A plot to check which distribution fits best. As you can see, the majority could not be fitted at all. Image: by author.

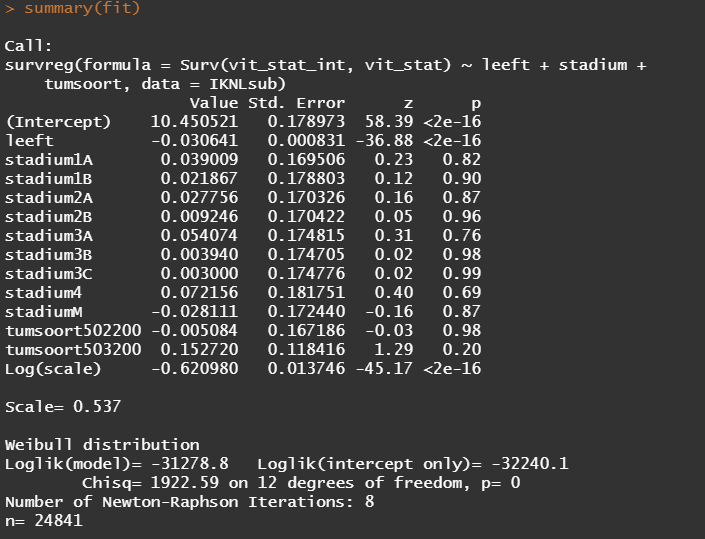
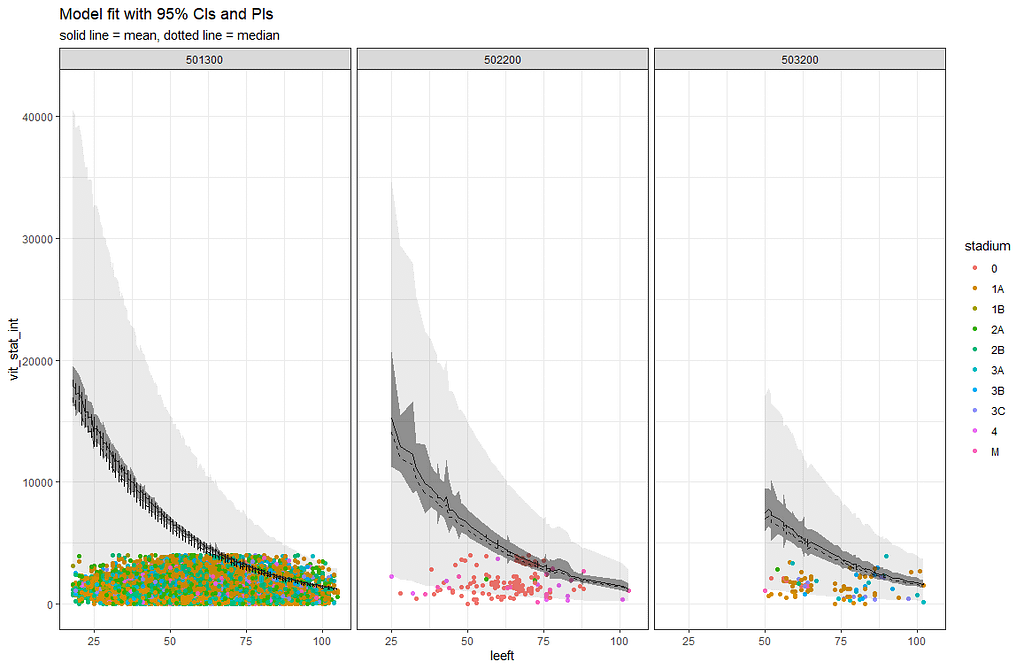
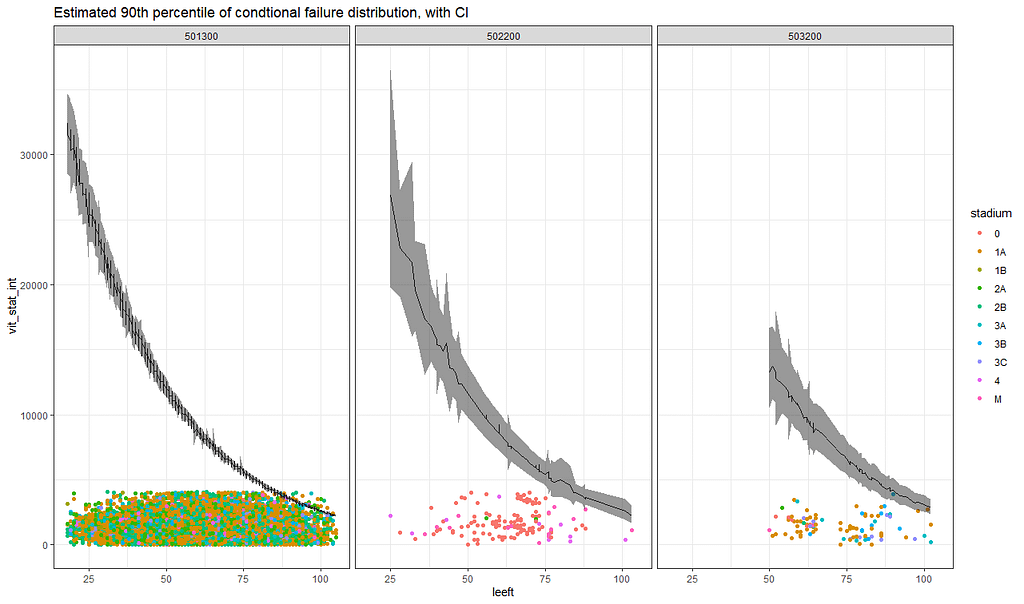
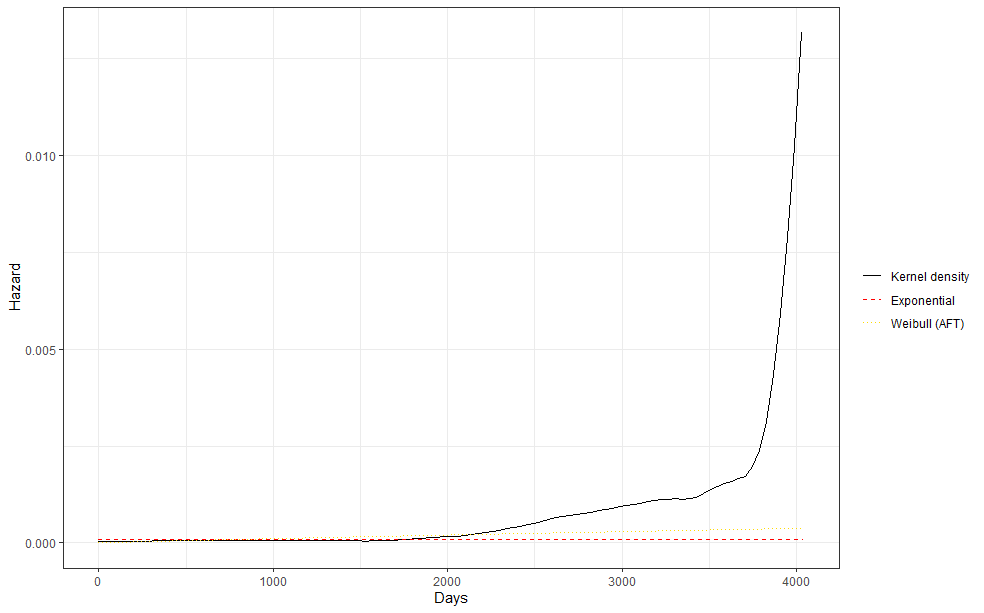
So, the parametric survival model did not really bring me something and perhaps the data are not so good for this kind of modeling anyway. Survival in Breast Cancer is quite high and a parametric survival model would by far extend beyond the data at hand. Most likely too far. So, let's stick to what we have, and seal the deal a bit.

Here, you see me building a nomogram — stable and dynamic using the RMS package and the DynNom package.

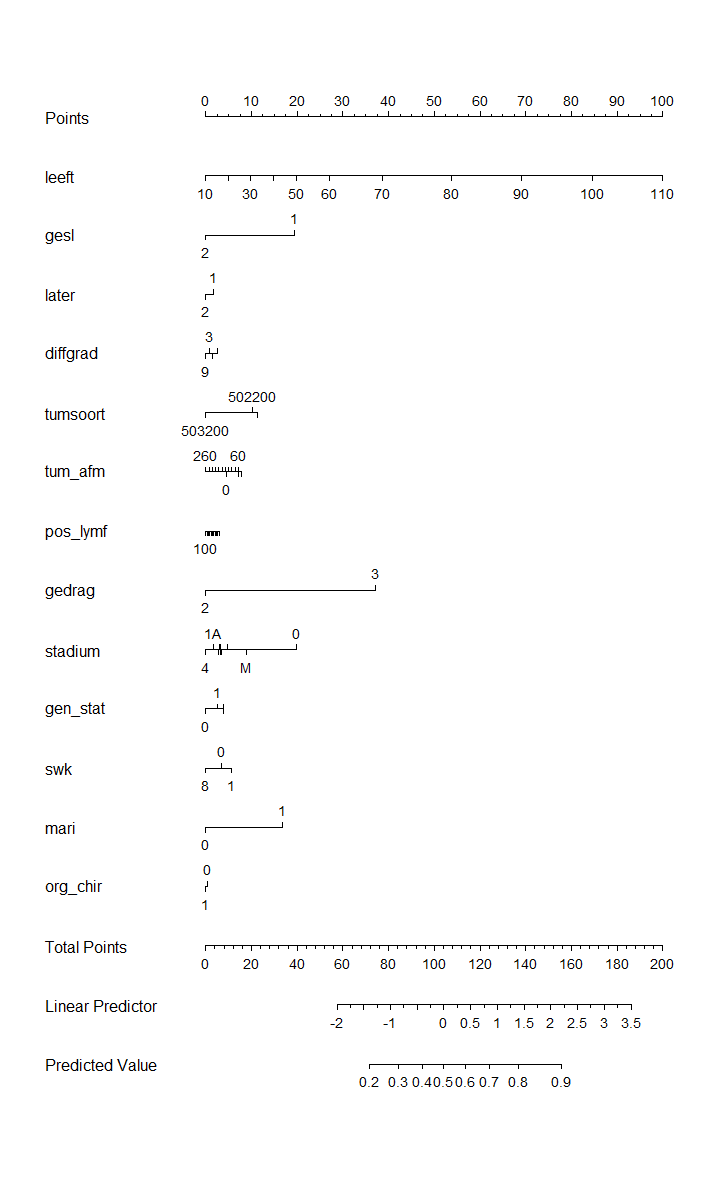
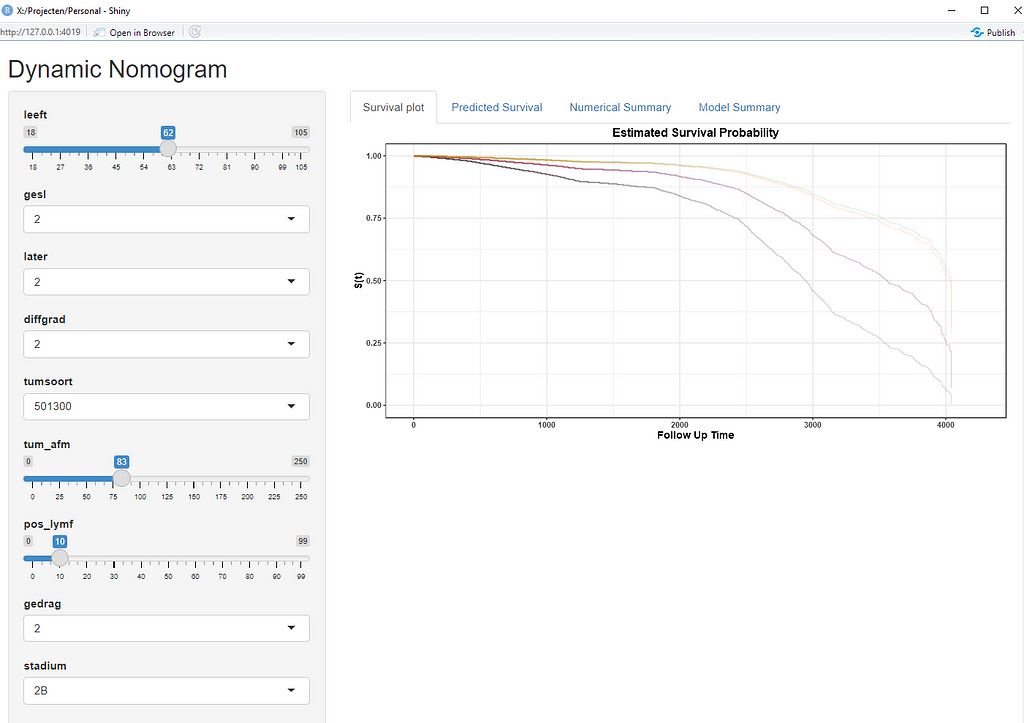
Good, so we now moved through the most important aspects of modeling this dataset, which are visual exploration, univariate survival models, multivariable cox regression models, model assessment and validation, penalization and variable importance, and parametric survival. Now I have shown what a potential sensible pathway could be towards a dynamic nomogram, which can be used in a clinical setting, lets rehash what we have learned and build a second tier of models.

It’s decision time. Let's make the model we want to have and focus a bit more. Based on the above, I will make the following choices:

Females only → although breast cancer is a possibility in men, we have more data on females.
Tumor kind 501300 only → the majority of the data is situated here.
Will not include the inclusion year — a proxy for survival
From the penalized models, only the following variables were deemed important: age, differential grade, tumor position, hormonal indicators, Mari-procedure, and tumor stage.
From the Random Forest Models, only the following variables were deemed important: age, Mari-procedure, tumor size, tumor stage, sentinel node procedure performed, surgery performed, number of positive lymph nodes found, differential grade, and hormonal receptors.

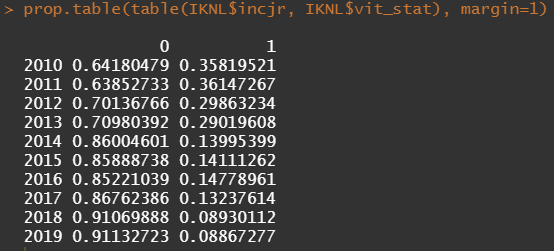
Let's try and re-verify the above by plotting some basic proportional tables. What I want to see is that the variables included show the same proportion of events and non-events across their levels. If this is the case then that variable has limited appeal.

First, check the proportions, within each row of the matrix for tumor kind, sex, lateralization, and inclusion year.

Looking good. Safe to focus only on females, and the tumor kind with the biggest data and the lowest survival rate. Image: by author.

Lateralization is indeed not a differentiating variable. Image: by author.

The inclusion year and event proportion. The number of events is highest for the earliest inclusion year which mirrors the survival time by itself. Including it as a proxy will hurt the analysis, so we indeed kick it out. Image: by author.

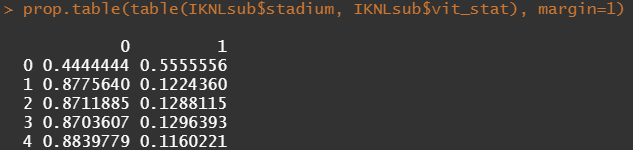
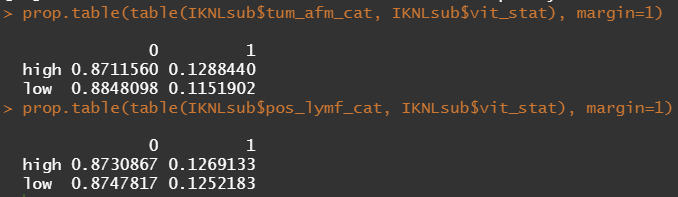
Then, let's look at the variables deemed important.

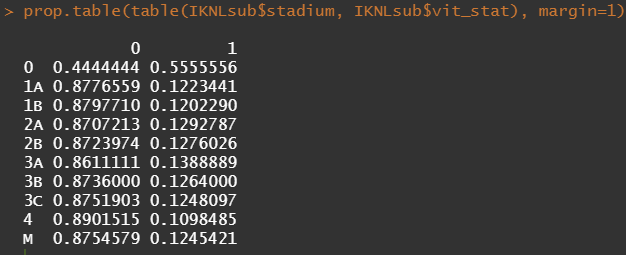
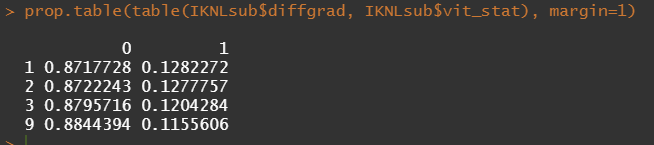
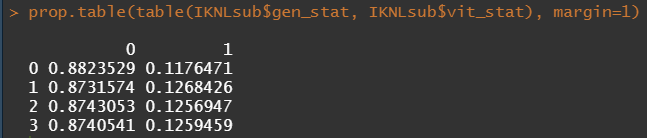
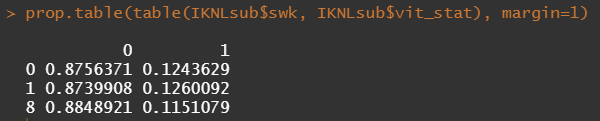
They do not show a lot of differentiation as well to be honest? Well, at least the majority do not while some have a major impact like tumor placement (**gedrag**). The problem with a 2*2 matrix is that it can really only show marginal effects, nothing very conditional. Image: by author.

To ease the model a bit, I will refactor some of the variables included to downplay the number of factors. I will also cut two continuous variables. Normally, this is really not a smart thing to do as you will lose predictive power, but for the sake of the prediction model, I might make sense.

Now, let's rerun the models and see where we will land. I will not be perfect, for sure, since this model is made without an oncologist or anybody else with a lot of content knowledge on how to treat breast cancer.

We should have enough events. Image: by author.

The model fit, containing one interaction between age and differential gradation. Image: by author.

The overal survival curve. Almost to zero. Image: by author.

Variance Inflation Factor. For sure some high levels. This model probably still has way to many variables included. Image: by author.

Not too bad, but I would like to reach above the magic threshold of 0.8. Lets later see how the calibration lines move. Image: by author.

Not too bad — not perfect either. Image: by author.

Hmm, the residuals look off at the end. Image: by author.

The calibration plot. There is this strange dent which I am pretty sure is caused by age, since age is a very big predictor for survival time, due to the fact that the older the less survival time (both in ability to deal with the cancer, but also just plainly the number of years left to live). Image: by author.

The nomogram, which attributes quite some weight on age, stage, tumor location, and if the Mari procedure was done. The rest not so interesting. Image: by author.

And the dynamic nomogram. Image: by author.

Here you see that every time I do a prediction, the curve is added, as well as the confidence interval and the table showing the risk profile. Image: by author.

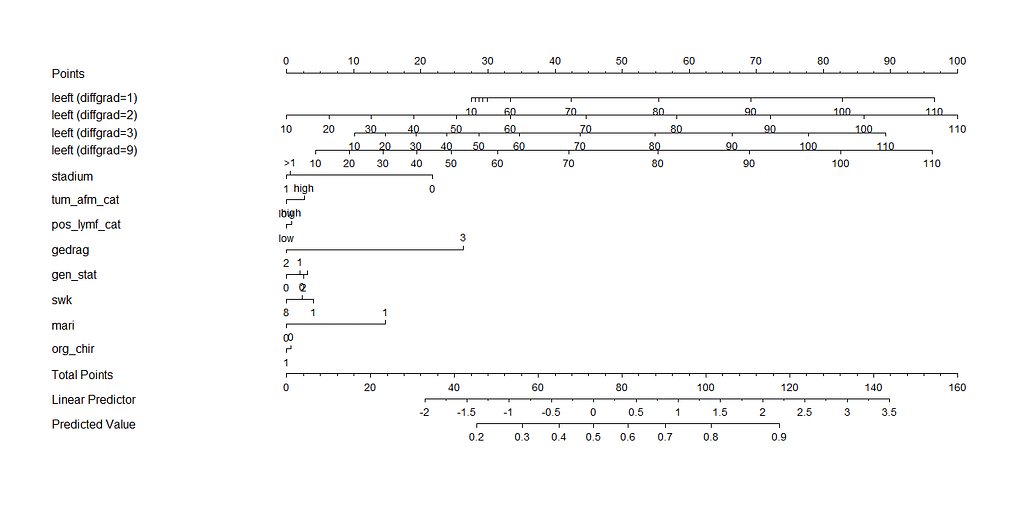
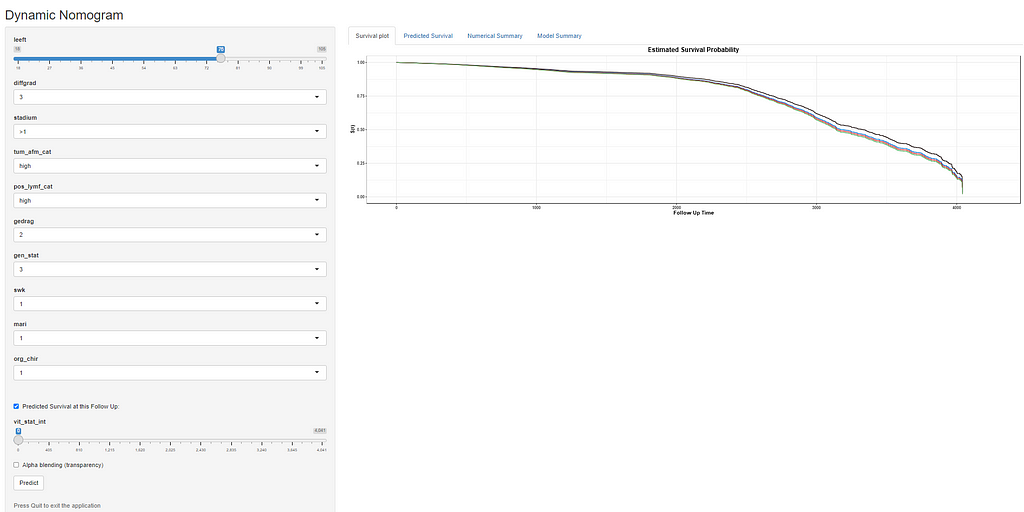
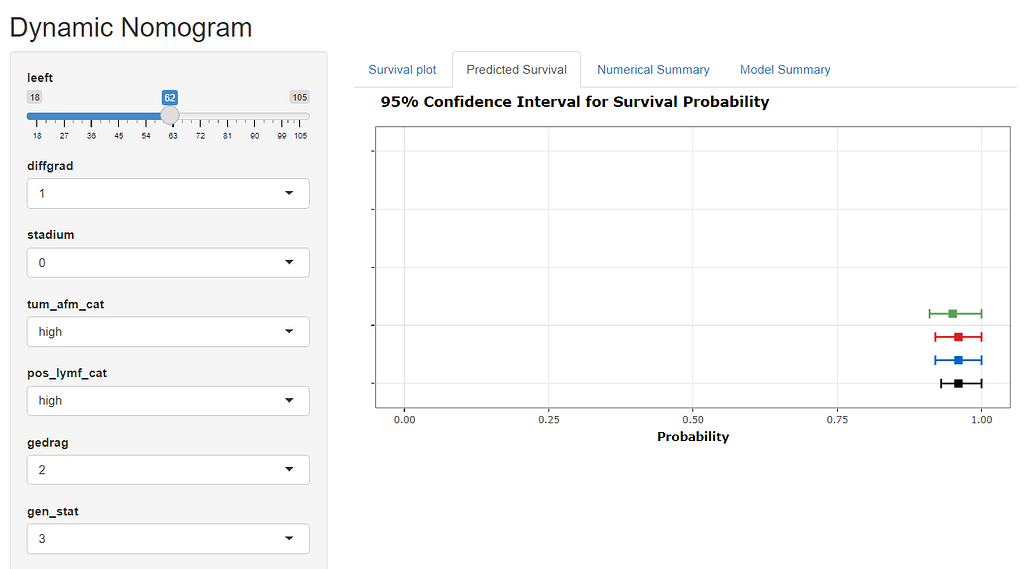
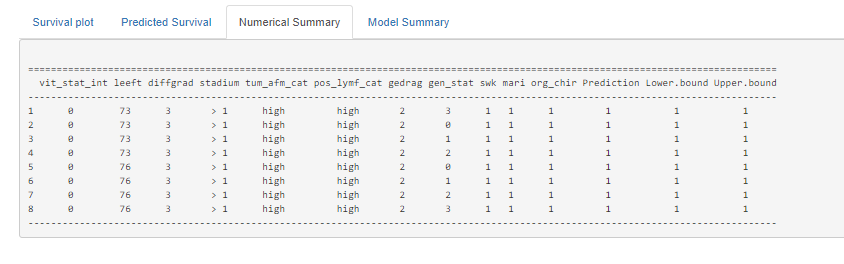
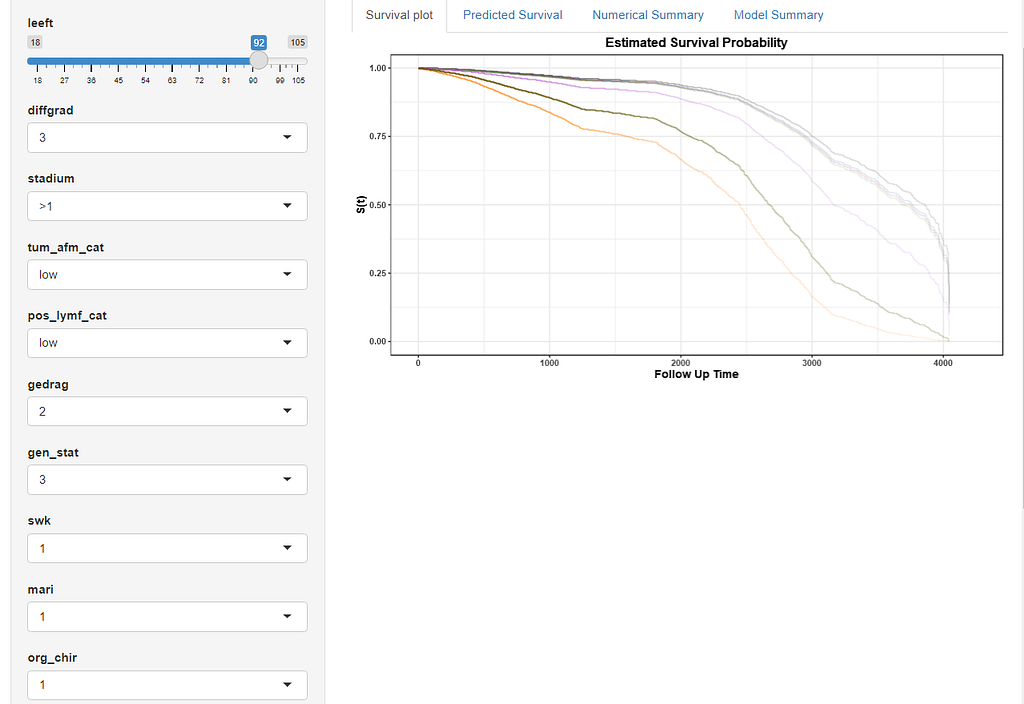
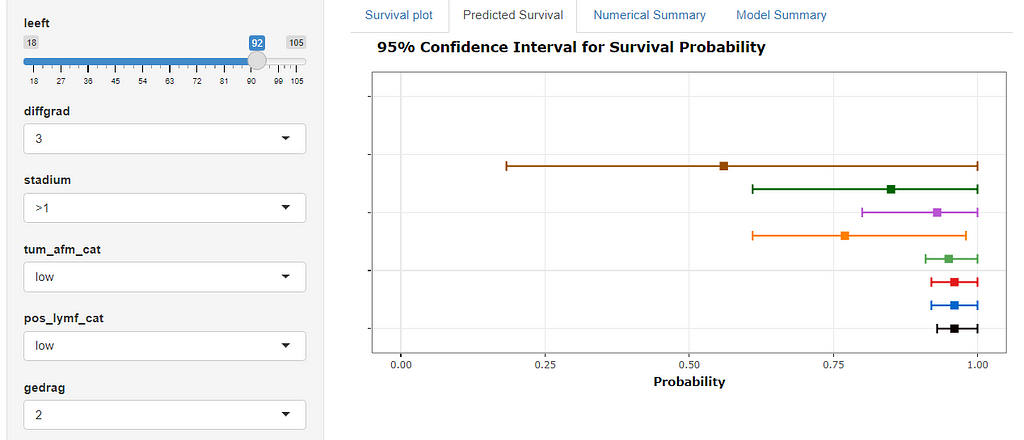
All right, folks, this is it for now. I am surely not done, but I need some time to contemplate. I will also dedicate a post on showing you how to host the Shiny app.

If something is amiss with this post, or there is a mistake or you have a question, you know where to find me!

Enjoy!

Analysis of a Synthetic Breast Cancer Dataset in R was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI

Frequently Used, Contextual References

Resources

Publication

Analysis of a Synthetic Breast Cancer Dataset in R

Author(s): Dr. Marc Jacobs

Data Analysis

Time-to-event data fully explored

Towards AI Team

Feedback ↓ Cancel reply

Popular posts

Best Laptops for Deep Learning, Machine Learning (ML), and Data Science for 2023

Best Workstations for Deep Learning, Data Science, and Machine Learning (ML) for 2022

Descriptive Statistics for Data-driven Decision Making with Python

Best Machine Learning (ML) Books - Free and Paid - Editorial Recommendations for 2022

Best Data Science Books - Free and Paid - Editorial Recommendations for 2022

Updates

Recent Posts

AI and Deepfakes in the Courtroom

A Guide to Integrating LLM Agent into POS Systems

Top Important LLM Papers for the Week from 01/04 to 07/04

7 Easy Tricks to Take Your ChatGPT Prompts to the Next Level

Top Important Computer Vision Papers for the Week from 01/04 to 07/04

The World’s Leading AI and Technology Publication.

Company

CONTACT US

Cookie	Duration	Description
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.

Frequently Used, Contextual References

Resources

Publication

Analysis of a Synthetic Breast Cancer Dataset in R

Author(s): Dr. Marc Jacobs

Time-to-event data fully explored

Towards AI Team

Related posts

Feedback ↓ Cancel reply

Popular posts

Updates

Recent Posts

The World’s Leading AI and Technology Publication.

Company

CONTACT US

GDPR CCPA Statement