Dreamer: A State-of-the-art Model-Based Reinforcement Learning Agent

Last Updated on May 31, 2020 by Editorial Team

Author(s): Sherwin Chen

Reinforcement Learning

A brief walk-through of a state-of-the-art model-based reinforcement learning algorithm

We discuss a model-based reinforcement learning agent called Dreamer, proposed by Hafner et al. at DeepMind that achieves state-of-the-art performance on a variety of image-based control tasks but requires much fewer samples than the contemporary model-free methods.

Overview

Dreamer is composed of three parts:

• Dynamics learning: As a model-based RL method, Dreamer learns a dynamics model consisting of four components: a representation model, a transition model, a reconstruction model, and a reward model.
• Behavior learning: Based on the dynamics model, Dreamer learns an actor-critic architecture to maximize rewards on imagined trajectories.
• Environment interaction: Dreamer interacts with the environment using the action model for data collection.

In the rest of the post, we will focus our attention on the first two parts, as the last soon becomes apparent after that.

Dynamics Learning

Dreamer represents the dynamics as a sequential model with the following components

In the rest of the post, we refer to the transition model as the prior and the representation model as the posterior since the latter is additionally conditioned on the observation.

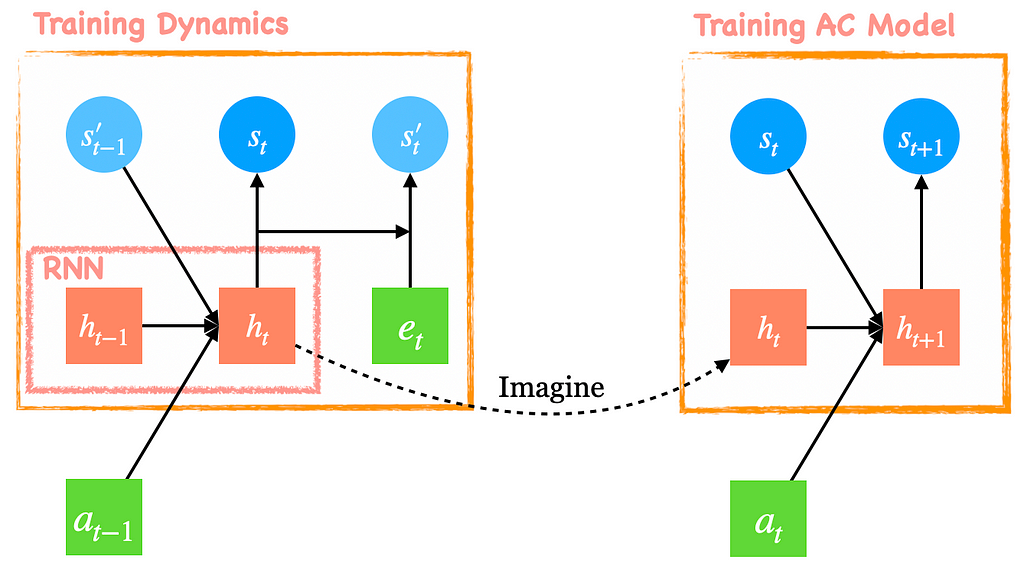
Like its predecessor, PlaNet, Dreamer adopts the recurrent state-space model(RSSM) as the world model, which splits the state space into stochastic and deterministic components. Figure 1 shows how the RSSM model is unrolled in a single time step. When training the dynamics model, the RNN takes as input the action a_{t-1} and posterior stochastic state s’_{t-1} from the previous time step and outputs a deterministic state h_t. The deterministic state h_t is then a) fed into an MLP with a single hidden layer to compute the prior stochastic state s_t; b) concatenated with the image embedding e_t and fed into another single-layer MLP to compute the posterior stochastic state. After that, we use the concatenation of h_t and s’_t as a start latent variable to reconstruct the image, reward, etc. Mathematically, we can divide the world model into the following parts.

One may also regard the RSSM model as a sequential VAE, where the latent variable at time step t is associated with that from the previous time step t-1 through the transition model. This gives us the following variational evidence lower bound(ELBO) objective.

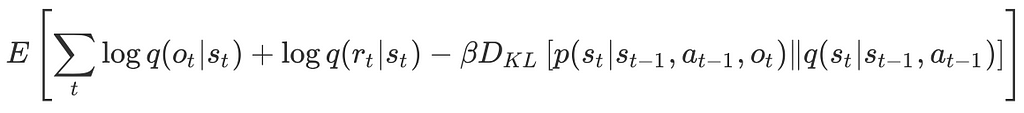
Maximizing this objective leads to model states that predicts the sequence of observations and rewards while limiting the amount of information extracted at each time step. This encourages the model to reconstruct each image by relying on information extracted at preceding time steps to the extent possible, and only accessing additional information from the current image when necessary. As a result, the information regularizer encourages the model to learn long-term dependencies.

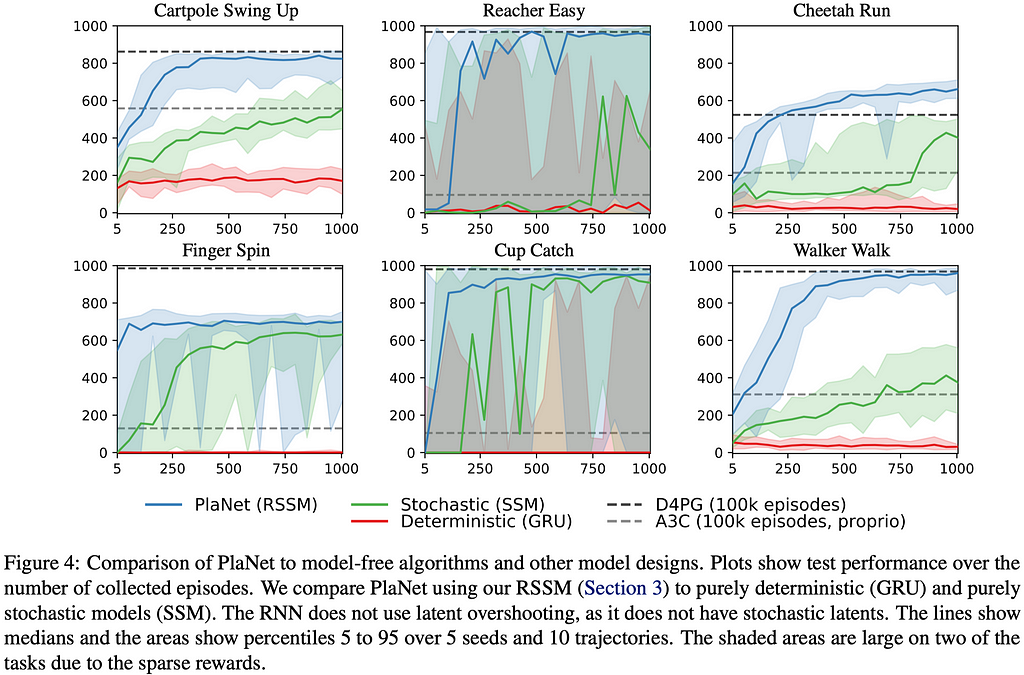
Before we move on, it is worth stressing that the deterministic and stochastic state models serve different purposes: The deterministic part reliably retains information across many time steps, based on which the stochastic part builds up a compact belief state of the environment. The latter is especially important as the environment is generally partially observable to the agent — Figure 4 shows that, without the stochastic part, the agent fails to learn anything!

Behavior Learning

Dreamer trains an actor-critic model on the state space for behavior learning. More specifically, Dreamer first imagines trajectories starting from some true model states s_𝜏 from the agent’s past experience, following the transition model q(s_{t+1}|s_t, a_t), policy q(a_t|s_t) and reward model q(r_t|s_t) — see Figure 1 right for illustration. Notice that, during imagination, the RNN takes as input the prior stochastic state since there is no more observation is given. We then train the actor-critic model by maximizing the expected returns along these trajectories with the following objectives

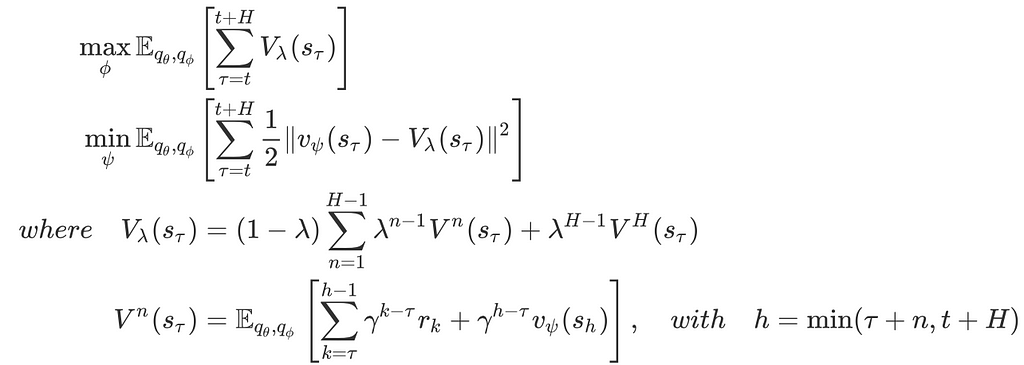
In fact, the choice of these RL objectives is quite brilliant. I’ve tried to apply some other off-policy methods to the latent space learned by Dreamer, such as SAC with retrace(𝝀), as I thought that function approximation errors introduced by the world model(i.e., the dynamics, reward, and discount models) might cause inaccurate predictions on the imagined trajectories, whereby impairing the performance of the AC model. However, the experimental results suggested an opposite story: learning from imagined trajectories outperforms applying off-policy methods on the latent space in terms of the learning speed and final performance. This is because learning from imagined trajectories provides richer training signals, facilitating the learning process; if we reduce the length of the imagined trajectories H to 1​, Dreamer performs worse than applying SAC to the latent space.

References

Danijar Hafner, Timothy Lillicrap, Jimmy Ba, Mohammad Norouzi. Dream to Control: Learning Behaviors by Latent Imagination. In ICLR 2020

Alexander A. Alemi, Ian Fischer, Joshua V. Dillon, Kevin Murphy. Deep Variational Information Bottleneck. In ICLR 2017

Acknowledgments

I’d like to especially thank Danijar Hafner for discussions with the code.

Dreamer was originally published in Towards AI — Multidisciplinary Science Journal on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI