The World’s First Computer Algorithm

Author(s): Bhavesh Agone

Originally published on Towards AI.

In a world where no computers yet existed, Ada Lovelace wrote the world’s first algorithm.

The First Glimpse of Programming & Complexity in the 1800s

The Analytical Engine weaves algebraic patterns just as the Jacquard loom weaves flowers and leaves.”
— Ada Lovelace, 1843

When we think of computers and algorithms, we see flickering silicon chips and Python scripts. But turn back close to 200 years, and you’ll discover the incredible tale of Ada Lovelace — the visionary person who envisioned a world where machines could calculate anything using logic, loops, and memory.

In 1843, Ada created what is widely considered the first computer algorithm: a set of instructions to compute Bernoulli numbers using Charles Babbage’s hypothetical mechanical computer — the Analytical Engine.

In this blog, we’ll break down her algorithm step by step, explore its mathematics, understand its flow, and analyze its computational complexity — all while appreciating just how ahead of her time she really was.

What Are Bernoulli Numbers?

Bernoulli numbers are a sequence of rational numbers important in number theory, calculus, and numerical analysis.

Bernoulli numbers are rational numbers defined by the generating function:

They appear in formulas like:

• Calculus (Taylor expansions)
• Sums of powers (Faulhaber’s formula)
• Numerical methods (Euler-Maclaurin formula)

Their recursive nature makes them a perfect candidate to show off an algorithm’s power — and that’s what Ada did.

Lovelace focused on odd-indexed numbers using a course-of-values recursion:

Important properties:
1. All odd-indexed Bernoulli numbers beyond B1​ are zero in modern definition.

2. Ada Lovelace used an alternative version: B1=-1/2, and computed odd-indexed values like B3,B5,B7,…

Ada Lovelace’s Algorithm — The Core Idea

Lovelace didn’t just state results — she wrote a procedural method, using what we’d now recognize as:

• Arithmetic operations
• Looping
• Indexed memory access
• Conditional jumps

Ada’s Recursive Algorithm:

Ada focused on computing odd-indexed Bernoulli numbers using a recursive formula (from Note G of her translation):

How it works:

• Upcoming numbers depends on previously computed odd-indexed Bernoulli numbers.

Each term in the sum is weighted by:

• A binomial coefficient
• A normalization denominator 2n−2k+1

Ada begins with B1=−1/2.

Example: Calculating B7:

To compute B7​, we use:

2n+1=7 ⇒n=3;

Known values:

From Ada’s own table (Note G), the Bernoulli numbers she used were:

• B1= −1/2
• B3= 1/6
• B5= −1/30

Now apply the formula:

Simplify each term:

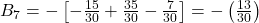
Important Clarification:

Correction: The actual value of B7is 1/42. Lovelace’s original calculation contained a minor error (likely due to transcription), but her method was sound.

This result differs from the modern value, where: B7​=0.

The difference comes from the definition of Bernoulli numbers in Ada’s time. She used a non-zero odd Bernoulli sequence based on their appearance in power sum formulas rather than the generating function.

Complexity Analysis

Time Complexity:

The formula is recursive:

• Outer loop runs n times
• Inner summation runs up to n terms
• Each term: constant-time arithmetic

Space Complexity:

Only stores n previous Bernoulli numbers:

Modern View of Bernoulli Numbers

In modern mathematics:

1. B1= -1/2

2. All odd-indexed Bernoulli numbers B{2n+1}​, for n≥1 are 0:

Modern implementations use:

• Generating functions
• Faulhaber’s formula
• FFT-based methods (like Harvey’s algorithm)

Ada Lovelace’s Contribution to Algorithms

Ada Lovelace was most innovative in developing a general-purpose, recursive algorithm — perhaps the very first one ever written with the intention of running on a machine.

Her computation of Bernoulli numbers not only added structured control flow, e.g., loops, nested loops, and indexed variables, but also addressed memory management within the constraints of the Analytical Engine.

She fashioned the algorithm to execute symbolically, with mathematical formulas that evolve with each iteration, embodying the modern notion of programmability and abstraction.

Ada’s algorithm was not hardcoded arithmetic — it was a general-purpose means of calculating any higher-order Bernoulli number, with evident aspects of modularity, reusability, and recursion. Her work positions her as foundational to algorithmic thought, years before the existence of digital computers.

Conclusion

Ada Lovelace’s algorithm was not just a mathematical exercise — it was the invention of programming. Employing symbolic logic, recursion, and a formal method of iteration, she described the first machine-executable algorithm decades before computers were invented. Although some of the numbers in her Bernoulli number table are different from those accepted now, her algorithm itself was mathematically correct and well ahead of its time.

Her tabulated minor mismatches are a result of changing conventions of mathematical notation, not a mistake in her reasoning. Her work actually introduced fundamental programming concepts: loops, conditionals, memory management, and abstraction.

Above all, Lovelace envisioned an era where computers could be programmed to handle not only numbers, but also ideas and symbols. That foresight, married with her detailed algorithmic style of thinking, is why she truly deserves the moniker as the world’s first programmer. Her Bernoulli number program was merely a starter — it marked the beginning of the age of programmable machines and, along with them, the digital world.

Some Addons:
1. The Analytical Engine was never actually built

2. Ada’s notes http://www.fourmilab.ch/babbage/sketch.html.

Please feel free to share your thoughts in the comment section. Your suggestions are always welcome.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI