Why convert text to a vector?

Author(s): vivek

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Mathematics

If you convert anything(text) to a vector by using some method so that we can use the power of linear algebra. But the main thing to think about is how do you convert text to vector? So that you can deploy the power of linear algebra to solve the problem.

How do you convert text to vector?

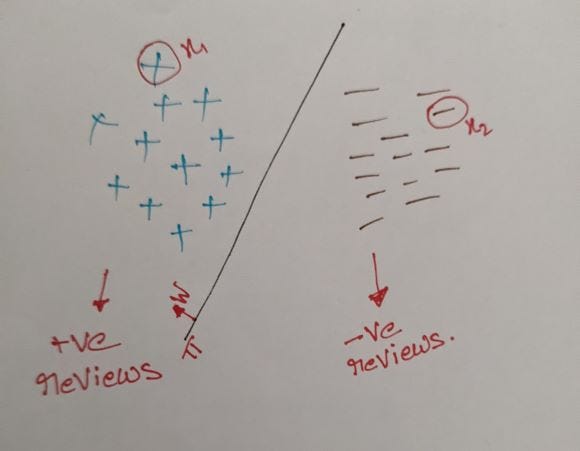
Here the text refers to both words and sentences and the vector refers to numerical vector. For example, we are having a review text, the aim is to convert it into a d-dimensional vector.

From the above figure consider

+ — positive review representation in d-dimensional space.

_ — negative review representation in d-dimensional space.

Keep a look at notations:

wTx — denotes w transpose x ( w Superscript T multiplied by x).

xi — denotes a point (x Subscript i ).

ri — denotes a review (r Subscript i ).

vi — denotes a vector ( v Subscript i ).

Consider all positive and negative reviews are in a d-dimensional plane which is separated by a plane Pi with a normal w. Let us assume that we can find a plan like this such that all the positive reviews are on one side and all the negative reviews are on the other side of the plane. By this, we can say that we found a model to solve the problem let’s say for the assumption.

We know that given any point x which is in the direction of the normal of the plane, then wTx for this point x is positive. Let us assume two points x1 and x2 where x1 represents the positive point and x2 represents a negative point. Then

WTx1: will be positive as the point lies in the direction of the normal of the plane.

WTx2: will be negative as the point lies in the opposite direction of the normal plane.

So, as per our assumption if all our points are in d-dimensional space and if we found a plane pi and normal w to it which divides the positive and negative points then we can say that,

If my wTxi > 0 the ri is positive else ri is negative.

Here, ri represents any review.

So, finally, we converted our text into a d-dimensional vector and found a plane that separates the text based on their polarity. The question is can we convert the text into d-dimensional space in any way or are there any set of rules to be followed for the conversion of text into a d-dimensional vector. The most important property(rule) to be followed is as follows,

Suppose we are having three reviews namely r1, r2, r3 which are in a d-dimensional space(vector) each having vectors v1, v2, v3 respectively. in which r1 and r3 are very Semantically Similar(SS) to r1 and r2 i.e.,

SS (r1, r3) > SS (r1, r2)

then distance(d) between the vectors v1 and v3 is less than the distance between the vectors v1 and v2.

d (v1, v3) < d (v1, v2)

So, if the reviews r1, r3 are more semantically similar the vectors v1, v3 must be close to each other.

SS (v1, v3) > SS (v1, v2)

which implies length (v1- v3) < length (v1- v2)

Which means similar points are closer.

Here arises another question why do we need our vectors to be closed rather than farther to conclude them as similar?

Why closer rather than farther?

Let’s refer to Fig1 once again if all of our positive reviews are close together as compared to the distance from all of our negative reviews and vice versa. Then it is very easier for us to find a plan that separates both reviews. Hence, we want similar reviews to be closer rather than farther.

So, the next question is how we find a method that converts text to a d-dimensional vector such that similar text must be closer(geometrically) to each other. Some techniques or strategies to convert text to a d-dimensional vector are:

1) Bag-of-Words (BoW).

2) Word2Vec (w2v).

3) Term frequency-inverse document frequency (tf-idf)

4) tf-idf w2v.

5) Average w2v.

We will discuss the strategies in upcoming blogs.

Thank you, Happy learning people.

Why convert text to a vector? was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI