Serum analysis

Last Updated on January 21, 2022 by Editorial Team

Author(s): Dr. Marc Jacobs

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Data Analysis

Hunting for a mixed model in R

In this post, I will show you, using commercial data, how I tried to model serum data coming from cows. The data I cannot share, unfortunately, but analysis of commercial data always shows you what real data looks like. Even when the design of the experiment was done with the biggest scrutiny possible, the modeling itself may still pose quite a challenge.

I will try to show the data as best as I can and write the codes in such a way that they can be used on your own dataset.

First, let's load the libraries I used. You do not need all of them to model the data adequately, but R has a way of allowing analyses to be done via multiple packages and some offer additional functionality on top of the other

## Loading packages 
rm(list = ls())
library(plyr)
library(sjPlot)
library(ggplot2)
library(lattice)
library(reshape2)
library(kml)
library(dplyr)
library(effects)
library(lme4)
library(sjmisc)
library(arm)
library(pbkrtest)
library(lmerTest)
library(lmtest)
library(AICcmodavg)
library(lubridate)
library(merTools)
library(piecewiseSEM)
require(parallel)  # parallel computing  
library(scales)    # for squish()
library(gridExtra)
library(coefplot)  # coefficient plots (not on CRAN)
library(coda)      # MCMC diagnostics
library(aods3)     # overdispersion diagnostics
library(plotMCMC)  # pretty plots from MCMC fits
library(bbmle)     # AICtab
library(nlme)
library(readxl)
library(readr)
library(lubridate)
library(sjPlot)
library(sjstats)

Then, I will load in the data and start looking into it.

SerumDairy <- read_delim("data.csv", delim = ";", 
                   escape_double = FALSE, trim_ws = TRUE)
SerumDairy$Treatment<-as.factor(SerumDairy$Treatment)
SerumDairy$Treatment<-factor(SerumDairy$Treatment, 
                             levels=c("1","2", "3","4","5","6"))
print(levels(SerumDairy$Treatment))
SerumDairy$Treatment<-factor(SerumDairy$Treatment, levels(SerumDairy$Treatment)[c(2:6,1)])
SerumDairy$Treatment<-factor(SerumDairy$Treatment, ordered=TRUE)
SerumDairy$Treatment_cont<-as.character(SerumDairy$Treatment)
SerumDairy$sample<-NULL
SerumDairy$collar<-NULL
SerumDairy$Zn.ppm <- gsub(",", "", SerumDairy$Zn.ppm) 
SerumDairy$Cu.ppm <- gsub(",", "", SerumDairy$Cu.ppm)
SerumDairy$Zn.ppm<-as.numeric(SerumDairy$Zn.ppm)
SerumDairy$Cu.ppm<-as.numeric(SerumDairy$Cu.ppm)
head(SerumDairy)
class(SerumDairy$date)
SerumDairy$date
SerumDairy$Daydiff<-dmy(SerumDairy$date)
SerumDairy$Daydiff<-SerumDairy$Daydiff-SerumDairy$Daydiff[1]
SerumDairy<-SerumDairy[order(SerumDairy$Cow),]
SerumDairy$Daydiff<-as.numeric(SerumDairy$Daydiff)
SerumDairyCompl<-SerumDairy[complete.cases(SerumDairy),]
SerumMelt<-melt(SerumDairy, id.vars=c("Day", "Daydiff", "Cow","Block", "Treatment"), 
                measure.vars=c("Zn.ppm", "Cu.ppm"))
SerumMelt$value <- gsub(",", "", SerumMelt$value) 
SerumMelt$value<-as.numeric(SerumMelt$value)

#Summarising data tabular
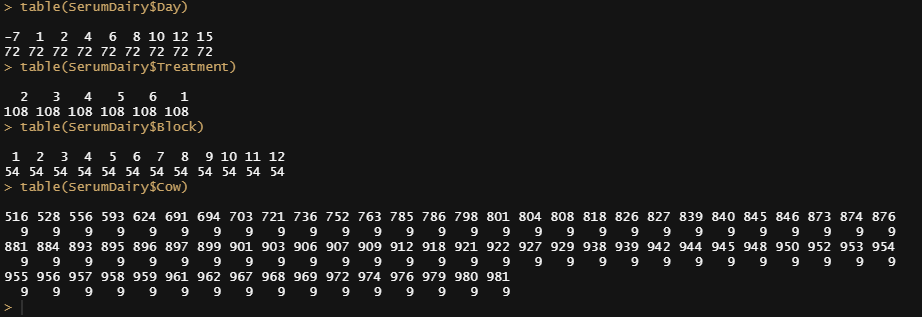
table(SerumDairy$Day)
table(SerumDairy$Treatment) 
table(SerumDairy$Block) 
table(SerumDairy$Cow)

As you can see, we have multiple measurements per day per cow per block. This was indeed a Randomized Complete Block Design.

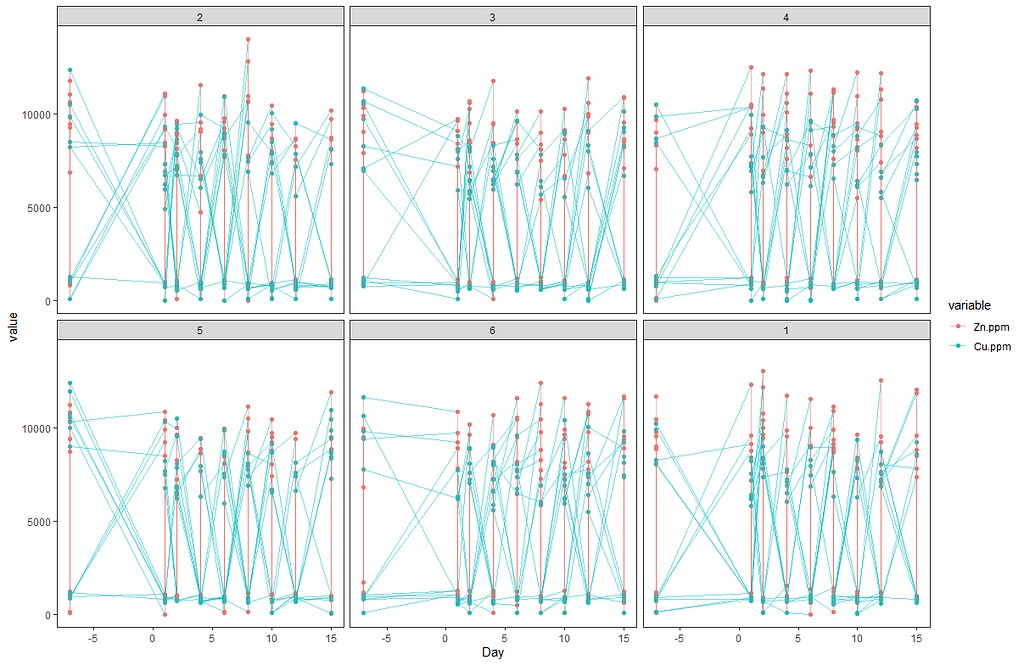
Off to the plots.

ggplot(SerumMelt, aes(x=Day, y=value, color=variable,group=Cow)) + 
  geom_point() + 
  geom_line(alpha=0.5)+
  theme_bw() +
  facet_wrap(~Treatment) + 
  theme(panel.grid.major = element_blank(), panel.grid.minor = element_blank()) +
  guides(linetype=F, size=F)

That is quite some funky data. The problem here is that I I modeled between treatments, but not blocks, which makes the data a little weird. Then again, it keeps going up and down, so I want to look closer at what it is that I am seeing.

# Plotting data 
dev.off()
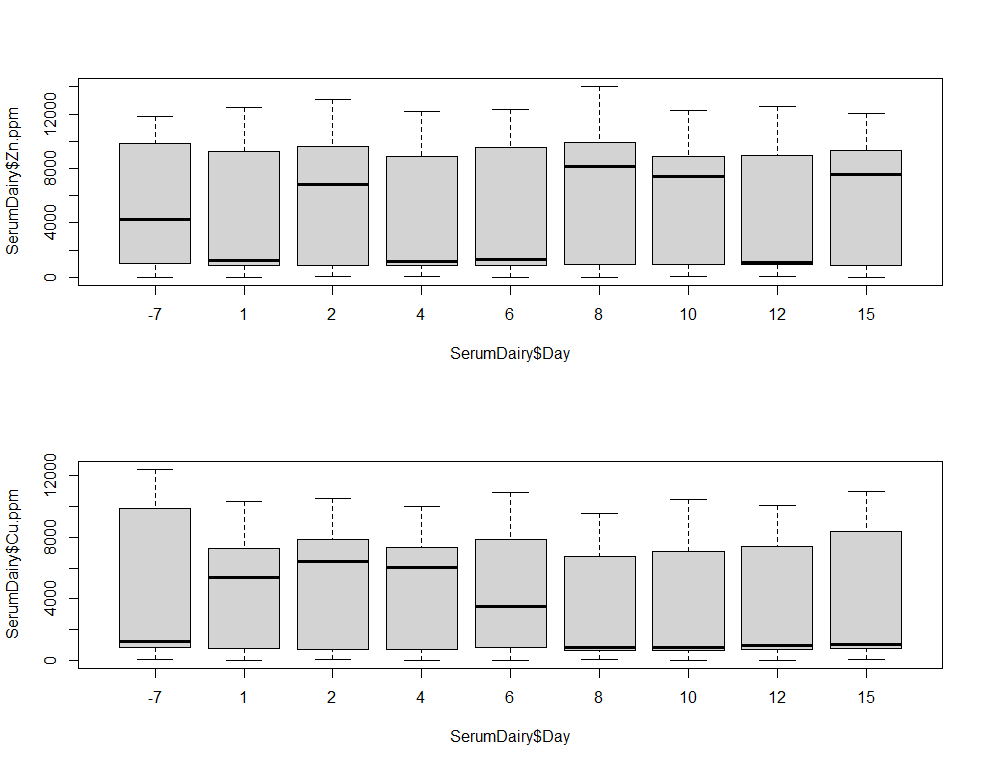
par(mfrow=c(2,1))
boxplot(SerumDairy$Zn.ppm~SerumDairy$Day)
boxplot(SerumDairy$Cu.ppm~SerumDairy$Day)
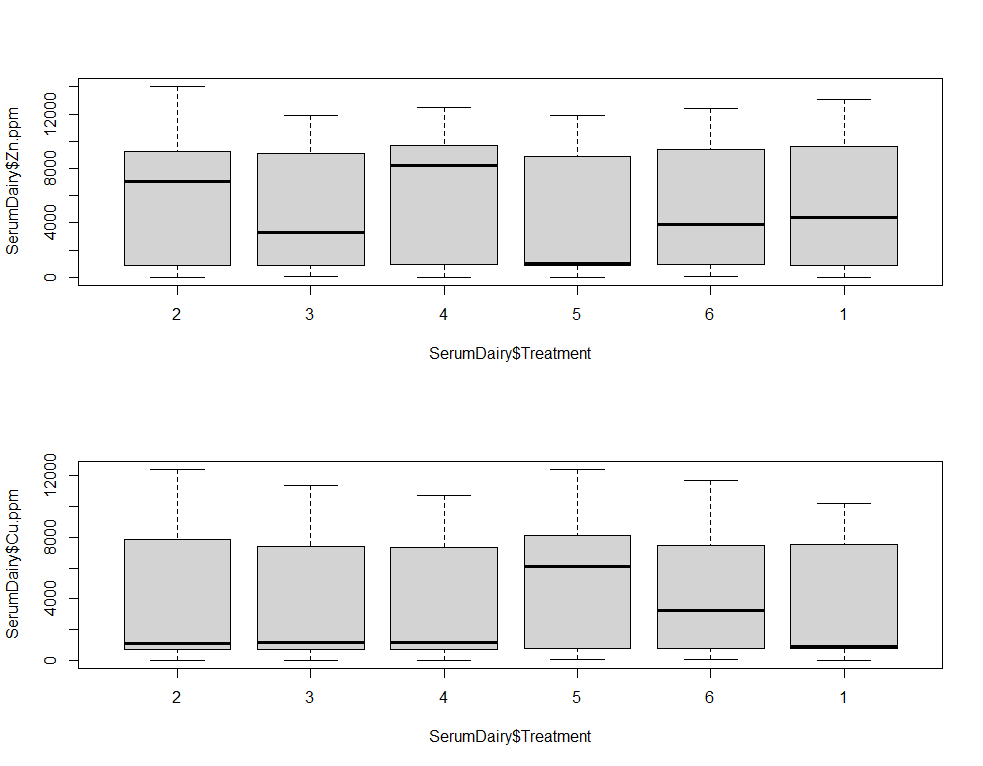
boxplot(SerumDairy$Zn.ppm~SerumDairy$Treatment)
boxplot(SerumDairy$Cu.ppm~SerumDairy$Treatment)
coplot(Zn.ppm~Day|Treatment, data=SerumDairy)
coplot(Zn.ppm~Day|Block, data=SerumDairy)
coplot(Cu.ppm~Day|Treatment, data=SerumDairy)
coplot(Cu.ppm~Day|Block, data=SerumDairy)

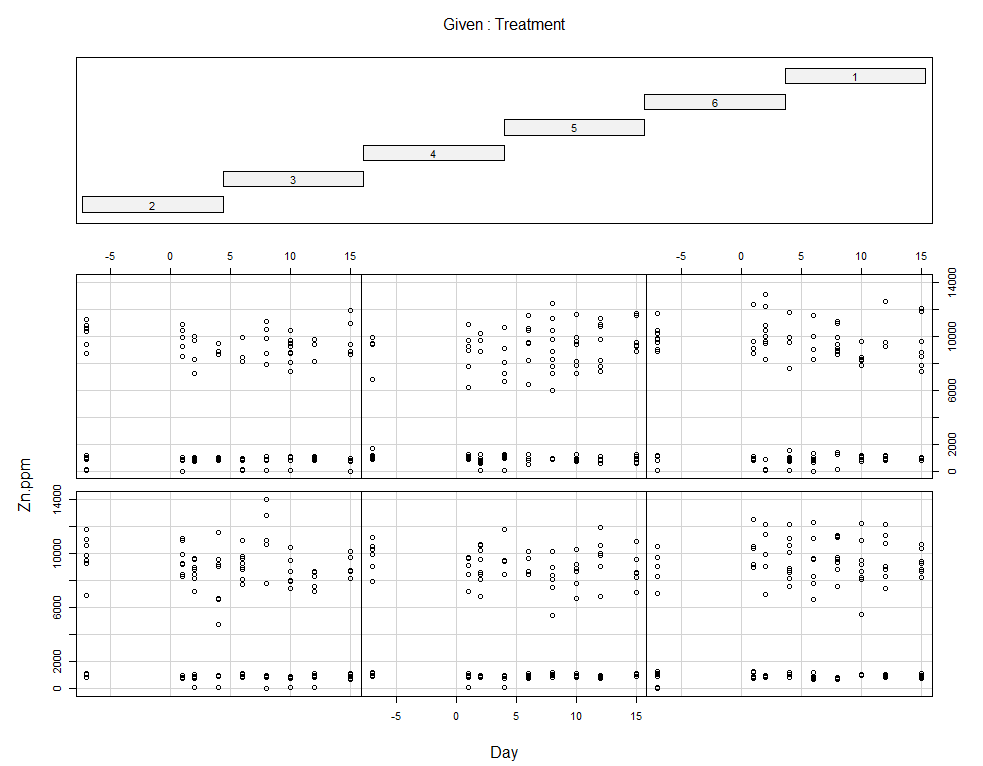
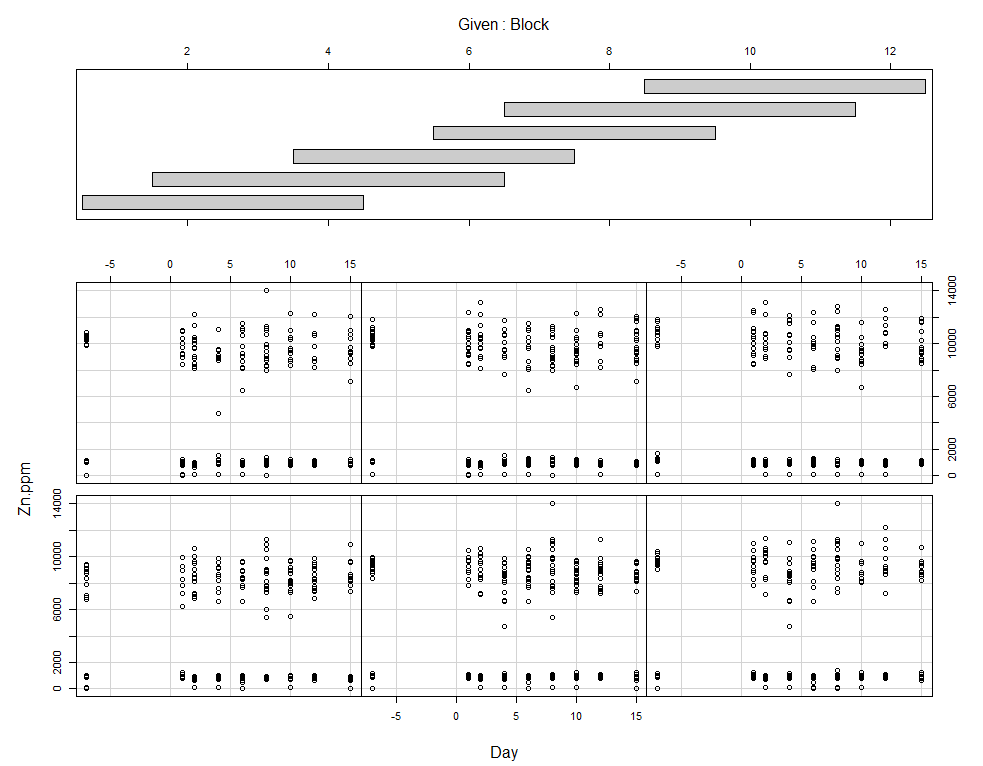
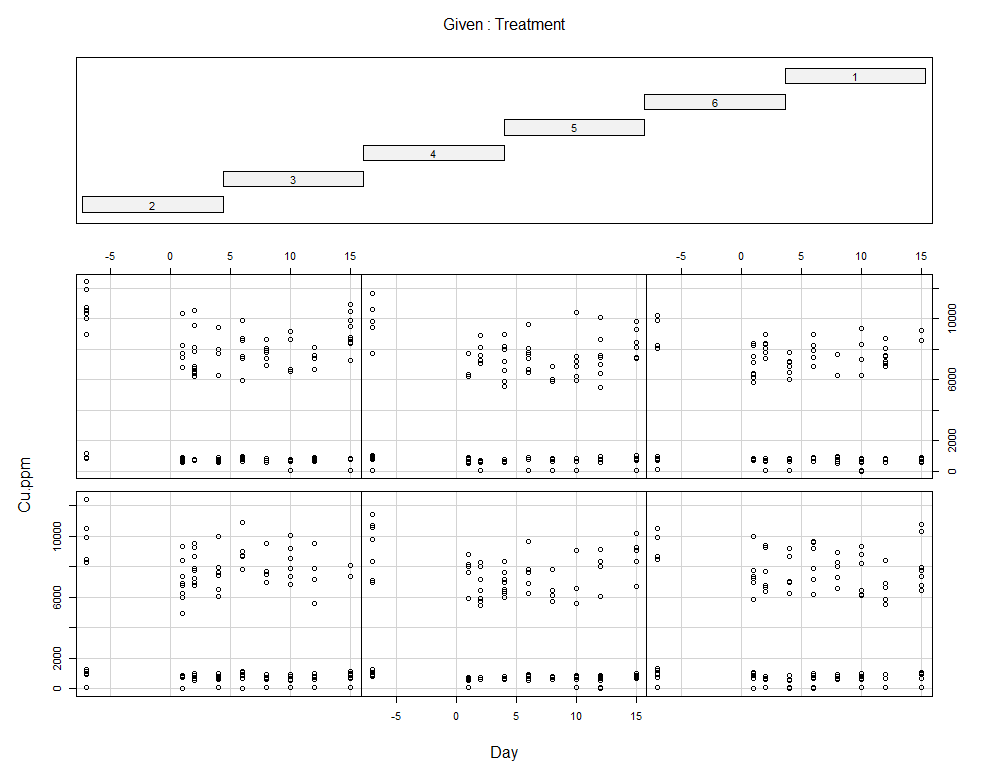
These plots help me get a better feeling about the individual parts of the data. I do not see any strange peaks.

Now, I want to plot some more to get a better even better idea. Remember, that first plot I made did not help at all.

# plotting Zn.ppm & Cu.ppm
ggplot(SerumMelt, aes(x=Day, y=value, group=Cow, color=variable)) + 
        geom_point(color="gray", shape=1)+ 
        geom_smooth(aes(group=variable, colour=variable), method="loess", size=1.5, se=F, span=0.5)+
        scale_y_continuous("Value") +
        scale_x_discrete("Days")+
        ggtitle(paste("Smoothed curves Zn.ppm & Cu.ppm"))+
        theme_bw()+
        facet_wrap(~Treatment)+
        theme(text=element_text(size=10), 
              axis.title.x = element_text(), 
              panel.grid.minor = element_blank())

ggplot(SerumMelt, aes(x=Day, y=value, fill=variable)) +
        geom_boxplot() +
        theme_bw()+
        theme(panel.grid.major = element_blank(), panel.grid.minor = element_blank())+
        ggtitle(paste("Boxplot of Zn.ppm & Cu.ppm by Days")) +
        scale_y_continuous("Value") +
        scale_x_discrete("Days") +
        facet_grid(~Treatment)+
theme(text=element_text(size=10), 
      axis.title.x = element_text(), 
      panel.grid.minor = element_blank())

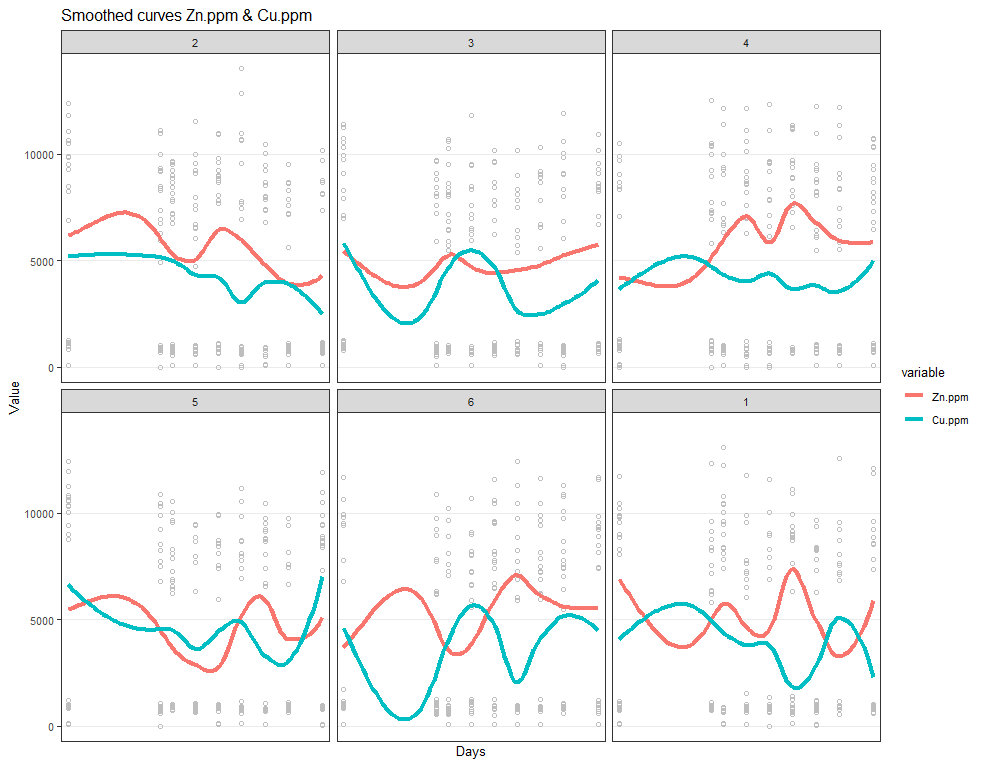
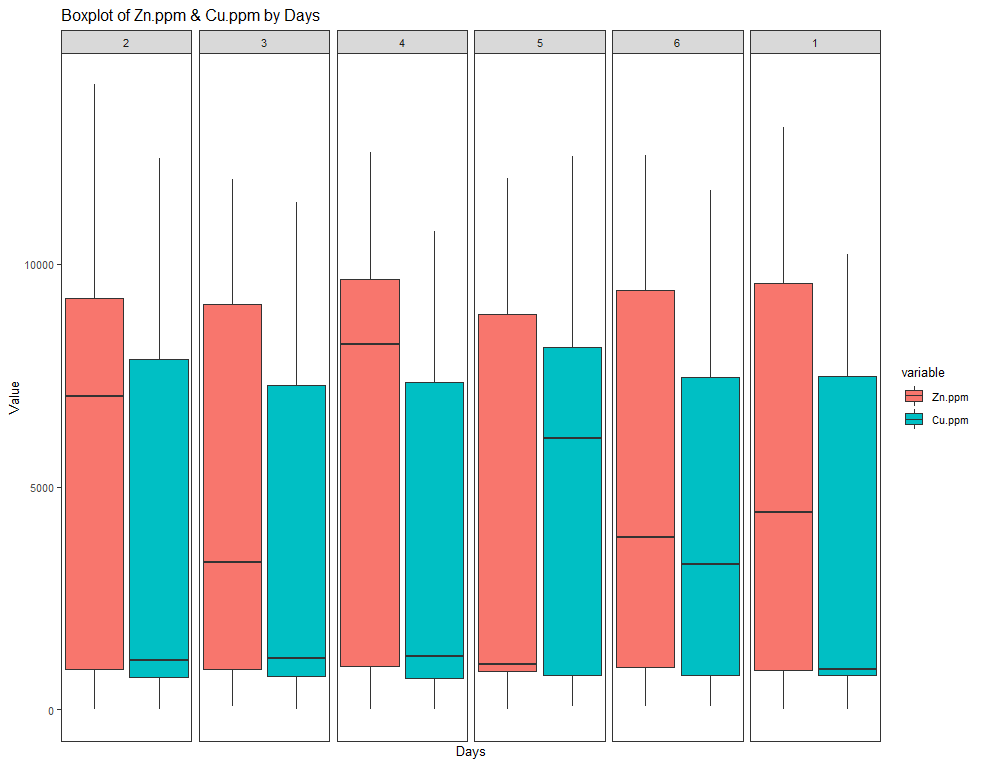
Although a LOESS smoother is always very cool looking, the box plot is much more informative in the sense that it shows an enormous amount of spread and a real gap in values that cannot be attained. This will make the analysis quite difficult, regardless of design.

Now, I want to look more closely at treatments.

# boxplot showing per treatment BW over time
ggplot(SerumDairy, aes(x=as.factor(Day), y=Zn.ppm, colour=as.factor(Treatment))) +
        geom_boxplot() +
        theme_bw() +
        ggtitle(paste("Boxplot of Zn.ppm by Days")) +
        scale_y_continuous("Zn.ppm") +
        scale_x_discrete("Days") +
        theme(text=element_text(size=10), 
              axis.title.x = element_text(), 
              panel.grid.minor = element_blank())

# line plot
ggplot(SerumDairy, aes(x=as.factor(Day), y=Zn.ppm, group=Cow)) + 
        geom_point(color="gray", shape=1) + 
        geom_smooth(aes(group=Treatment, colour=as.factor(Treatment)), method="loess", size=1.5, se=F, span=0.5) +
        scale_y_continuous("Zn.ppm") +
        scale_x_discrete("Days")+
        ggtitle(paste("Smoothed curve Zn.ppm"))+
        theme_bw()+
        facet_wrap(~Block)+
        theme(text=element_text(size=10), 
              axis.title.x = element_text(), 
              panel.grid.minor = element_blank())

ggplot(SerumDairy, aes(x=Daydiff, y=Zn.ppm, group=Cow, colour=Treatment)) + 
        geom_point(color="gray", shape=1) + 
        geom_smooth(aes(group=1), size=1.5, se=F, alpha=0.8, span=0.5) +
        facet_wrap(~Treatment)+
        theme_bw()

The middle plot shows the strange up-and-down pattern we saw in the first plot, which accumulates in the box plot to the left. Combined, those two plots show the uselessness of the LOESS graph to the right, and its dangerous if you would use it as the sole plot.

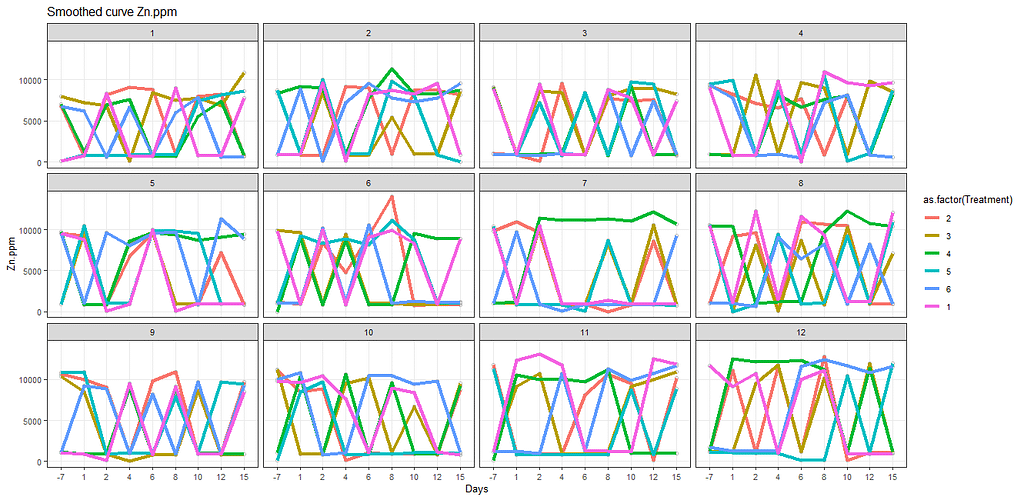
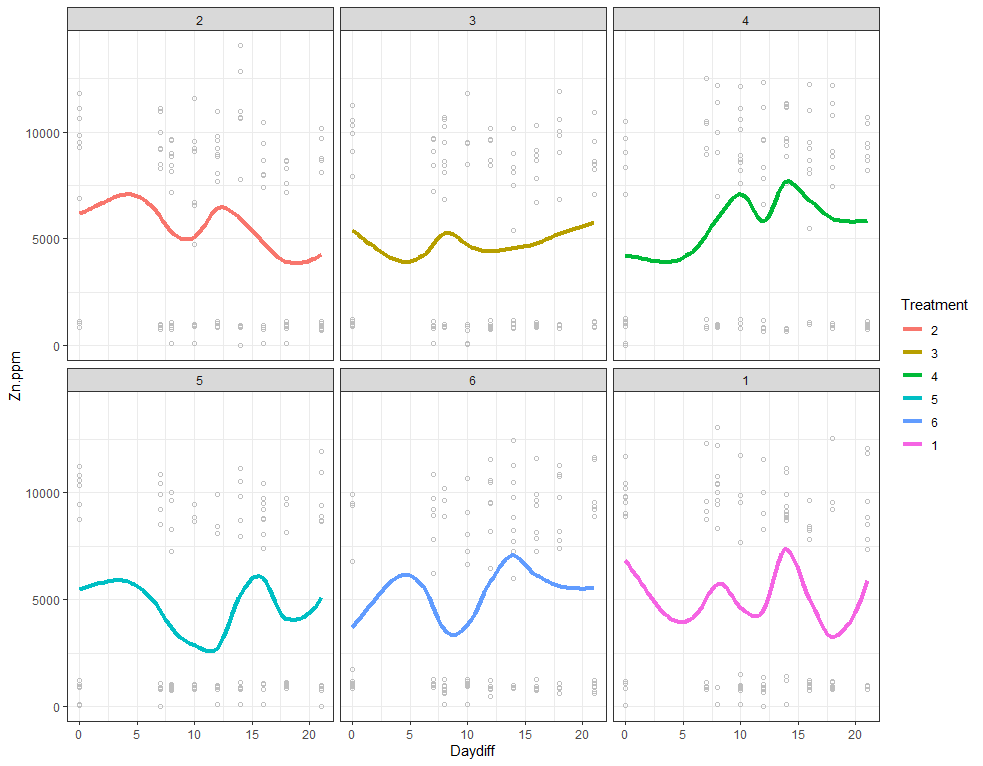
The next plots are perhaps the handiest for looking at the treatment data. Not because they try to picture the mean impact each treatment has, but also because they show the sheer level of variance already hinted at in the boxplots. Boxplots, for that matter, is perhaps the most inclusive plots to make.

# nicest line plot for Treatment
theme_set(theme_bw())
myx<-scale_x_continuous(breaks=c(0,7,8,10,12,14,16,18,21))
ggplot(SerumDairyCompl, aes(x=Daydiff, y=Zn.ppm, group=Cow))+
        myx+
        geom_line(colour="grey80") +
        facet_grid(~Treatment, margins=T)+
        stat_summary(aes(group=1), fun.y=mean, geom="point", size=3.5)+
        stat_summary(aes(group=1), fun.y=mean, geom="line", lwd=1.5)

theme_set(theme_bw())
myx<-scale_x_continuous(breaks=c(0,7,8,10,12,14,16,18,21))
ggplot(SerumDairyCompl, aes(x=Daydiff, y=Zn.ppm, group=Cow))+
        myx+
        geom_line(colour="grey80") +
        stat_summary(aes(group=Treatment, colour=Treatment), fun.y=mean, geom="point", size=3.5)+
        stat_summary(aes(group=Treatment, colour=Treatment), fun.y=mean, geom="line", lwd=1.5)

# nicest line plot for Block
theme_set(theme_bw())
myx<-scale_x_continuous(breaks=c(0,7,8,10,12,14,16,18,21))
ggplot(SerumDairyCompl, aes(x=Daydiff, y=Zn.ppm, group=Cow))+
        myx+
        geom_line(colour="grey80") +
        facet_grid(~Block, margins=T)+
        stat_summary(aes(group=1), fun.y=mean, geom="point", size=3.5)+
        stat_summary(aes(group=1), fun.y=mean, geom="line", lwd=1.5)

xyplot(SerumMelt$value~SerumMelt$Daydiff|SerumMelt$Treatment, type=c("p", "smooth"))
histogram(~SerumDairy$Zn.ppm|SerumDairy$Day+SerumDairy$Treatment)

Once again, the treatment data is very funky. It makes me wonder if the selected times were that helpful.

This plot clearly shows the variance in a pattern.

And, last and least, the smoothed curve which adds so little but tries so hard.

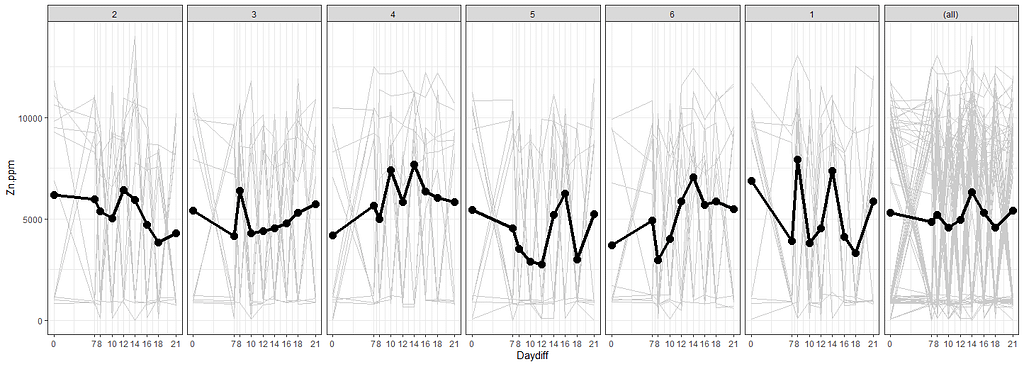
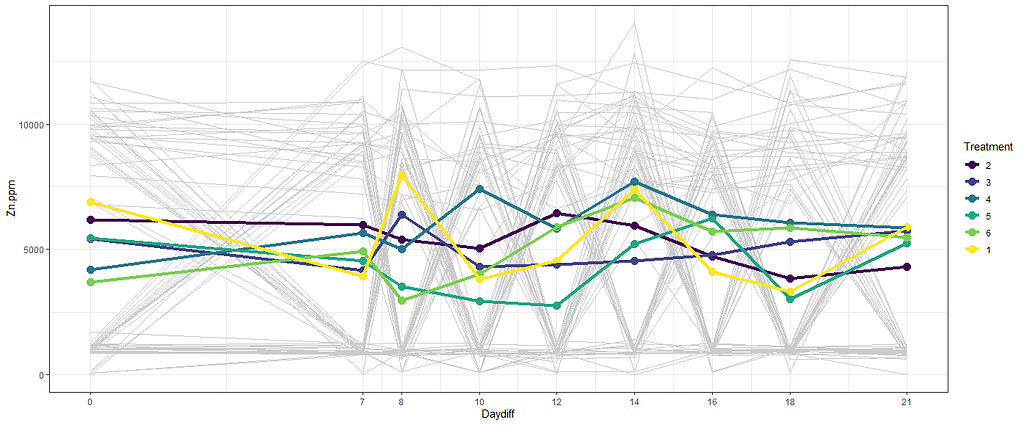
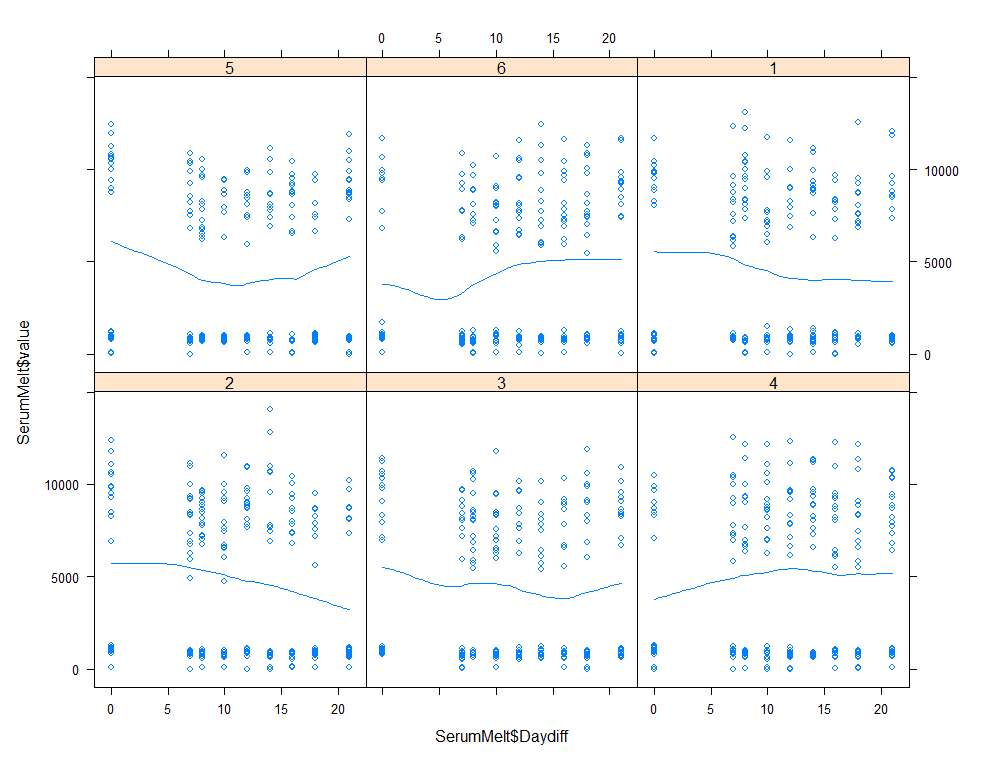
The time for graphs has come and I want to start modeling now, using Linear Mixed Models to take into account the correlated nature of the data via repeated measures.

First, some simple regression to get a better idea of how the models will deal with the different components of the design.

### Linear Mixed Models
## Zinc 
# Linear model for exploring data
SerumDairy$Daydiff<-as.numeric(as.character(SerumDairy$Daydiff))
class(SerumDairy$Daydiff)
SerumDairy$Treatment<-factor(SerumDairy$Treatment, ordered=FALSE)
summary(regr1<-lm(Zn.ppm~Daydiff, data=SerumDairy))
summary(regr2<-lm(Zn.ppm~Daydiff*Treatment, data=SerumDairy))
summary(regr3<-lm(Zn.ppm~Daydiff*Block, data=SerumDairy))
summary(regr4<-lm(Zn.ppm~Daydiff*Treatment*Block, data=SerumDairy))
plot(allEffects(regr1))
plot(allEffects(regr2))
plot(allEffects(regr3))
plot(allEffects(regr4))
anova(regr1, regr2, regr3, regr4)

Effect of day and treatment across blocks. If you look at the last post, you get a better feeling of the data and the variance that is inherent to it.

As you can see, all models are not statistically significant when compared to the first model which just includes day. Looking at the data, it makes sense, but we have not included the correlated structure yet.

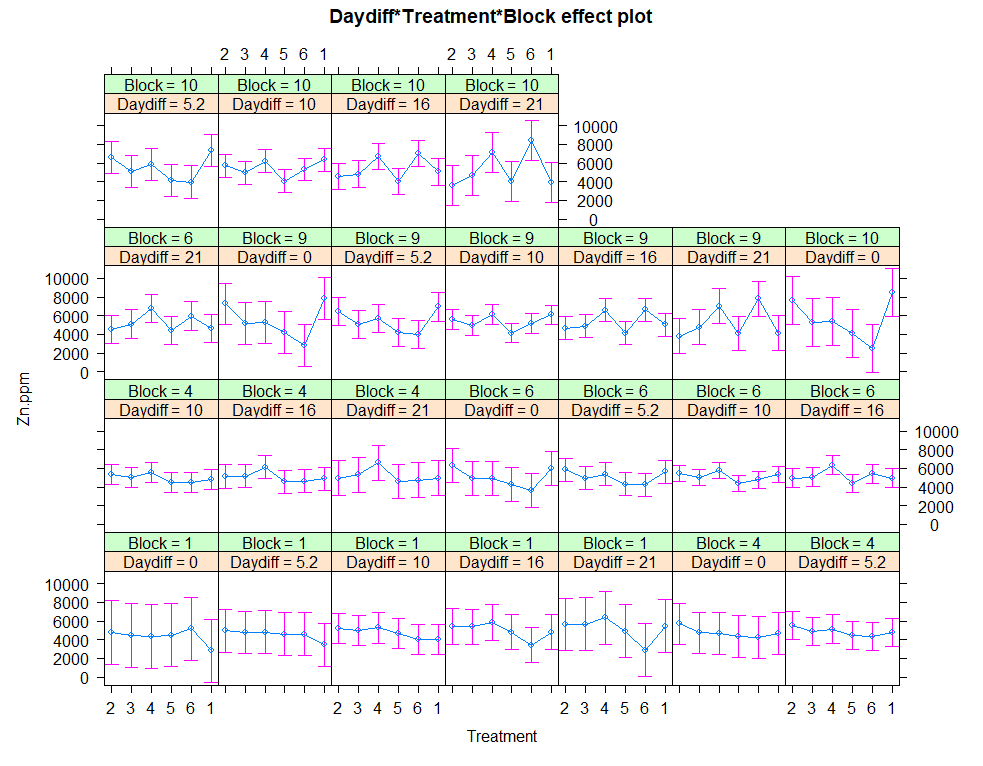
Let's continue and build unconditional growth models.

# Unconditional means model - intercept only model
model.i<-lmer(Zn.ppm~1 + (1|Cow), SerumDairy, REML=FALSE)

# Unconditional growth model - linear effect of time
model.l<-lmer(Zn.ppm~1 + Daydiff + (1|Cow), SerumDairyCompl, REML=FALSE) # random intercept + fixed time

# Unconditional polynomial growth model - quadratic effect of time
model.q<-lmer(Zn.ppm~1 + Daydiff + I(Daydiff^2) + (1|Cow), SerumDairy, REML=FALSE)

# comparing the unconditional mean model, the unconditional growth model, and the unconditional polynomial growth model
mynames<-c("I", "L", "Q")
myaicc<-as.data.frame(aictab(cand.set=list(model.i,model.l,model.q), modnames=mynames))[, -c(5,7)]
myaicc$eratio<-max(myaicc$AICcWt)/myaicc$AICcWt
data.frame(Model=myaicc[,1],round(myaicc[, 2:7],4))

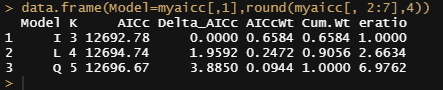
The first model, linear, seems to be the best.

I will then continue adding random slopes to the models.


model.l<-lmer(Zn.ppm~1 + Daydiff + (1|Cow), SerumDairyCompl, REML=FALSE) 
model.lr<-lmer(Zn.ppm~1 + Daydiff + (1+Daydiff|Cow), SerumDairyCompl, REML=FALSE) 
anova(model.l, model.lr) 
PBmodcomp(model.lr, model.l, nsim=1000, cl=cl)

plot_model(model.lr, facet.grid=F, sort.est="sort.all", y.offset=1.0)

plot_model(model.lr, type="est"); 
plot_modelr(model.4, type="std") 
plot_model(model.lr, type="eff") 
plot_model(model.lr, type="pred", facet.grid=F, vars=c("Daydiff", "Treatment"))

ranef(model.lr)
fixef(model.lr)

sam<-sample(SerumDairy$Cow, 15);sam
plot_model(model.lr, type="slope", facet.grid = F, sample.n=sam) # plotting random intercepts
plot_model(model.lr, type="resid", facet.grid = F, sample.n=sam) # plotting random intercepts but does not work?? 
plot_model(model.lr, type="diag")

The random slope component is not significant in a straightforward Likelihood Ratio Test, but it is when we due permutations of the data via bootstrapping. For now, it is perhaps best to keep the mixed model with the random intercept and the random slope.

The residuals are far from what you would like to see, although the random components do follow normality.

The residuals hint at a mismatched model, almost as if a mixture is needed.

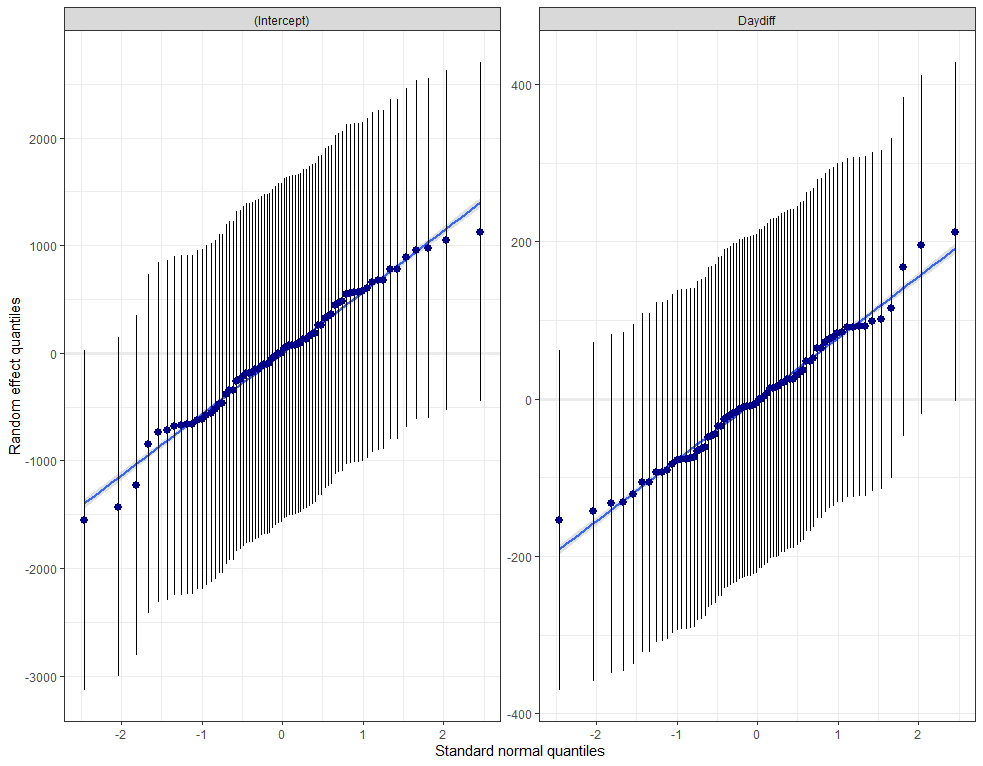
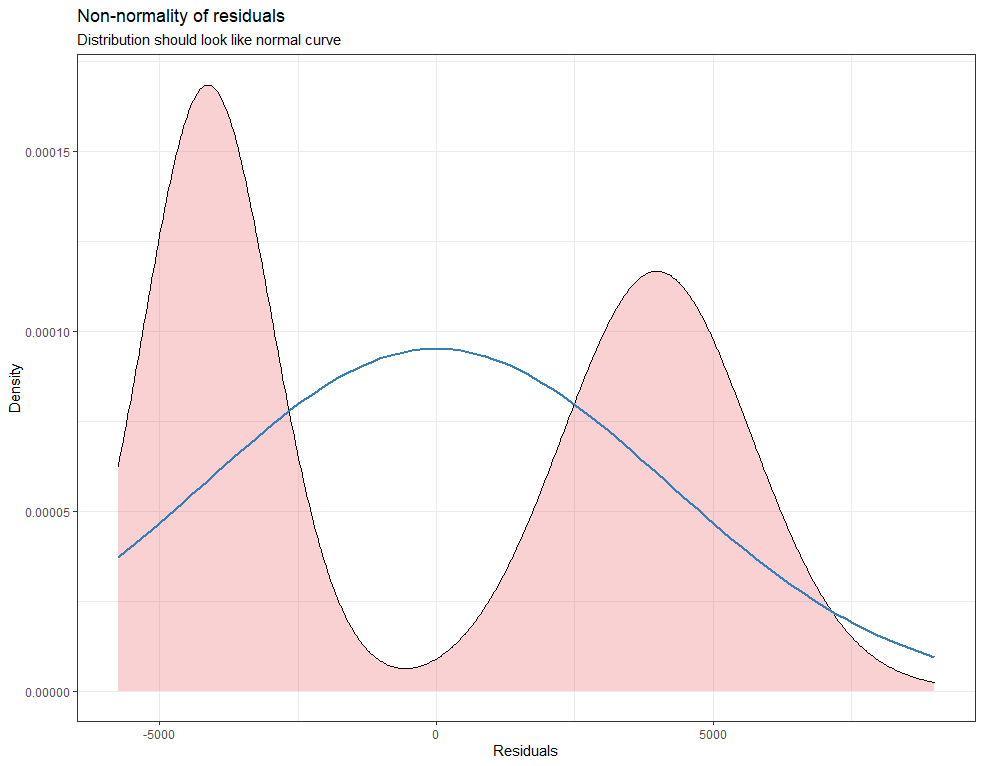
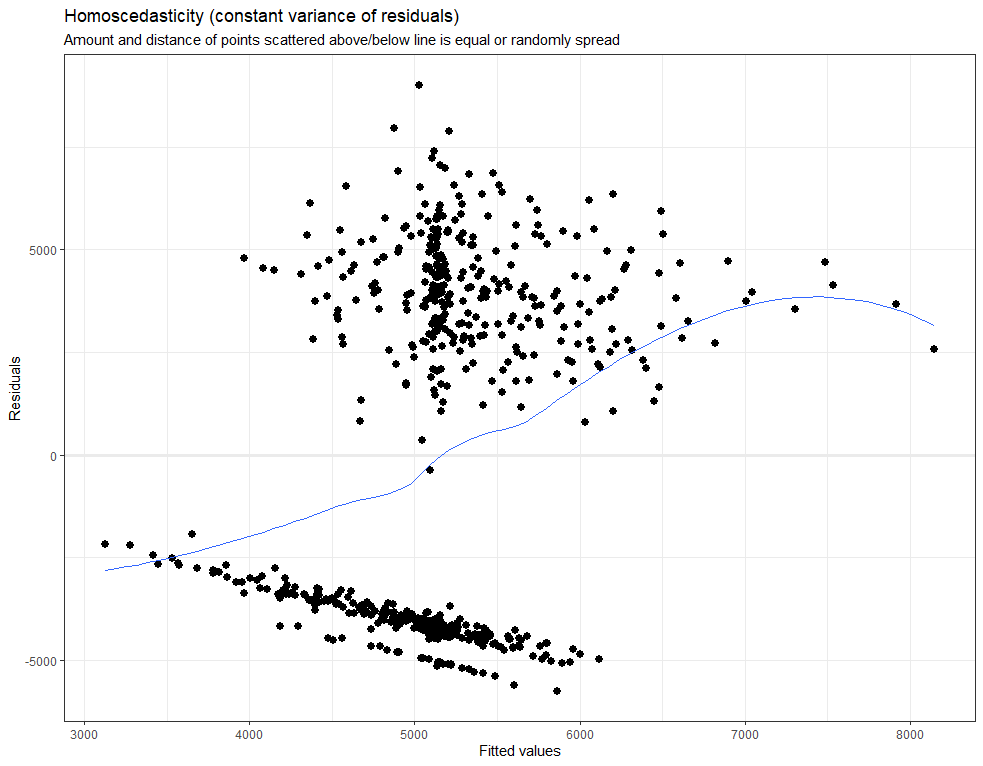
model.qr<-lmer(Zn.ppm~1 + Daydiff + I(Daydiff^2) + (1+Daydiff|Cow), SerumDairyCompl, REML=FALSE)
summary(model.qr) 
anova(model.l, model.q, model.lr, model.qr)

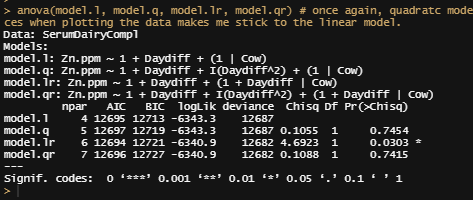
Well, the difference between models is microscopic. Best to apply Ocam’s razor.

I will now add the treatment effect

## Adding treatment effect
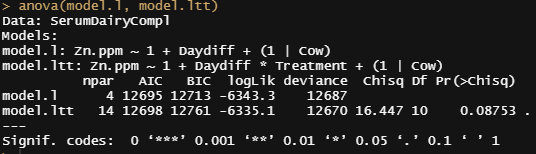
model.ltt<-lmer(Zn.ppm~1 + Daydiff*Treatment + (1|Cow), SerumDairyCompl, REML=FALSE)
summary(model.ltt)
anova(model.l, model.ltt)

Did not help one single bit. Although the p-value might hint at potential significance, the AIC barely changes.

# plotting time over treatments and blocks 
pd <- position_dodge(width = 0.2)
ggplot(SerumDairy, aes(x=Daydiff, y=Zn.ppm, group=Cow, color=Treatment))+ geom_point(position=pd) + geom_line(position=pd) + facet_grid(Treatment~Block)
ggplot(SerumDairy, aes(x=Daydiff, y=Zn.ppm, group=Cow, color=Treatment))+ geom_point(position=pd) + geom_line(position=pd) + facet_wrap(~Block)
plot(allEffects(model.5))
eff.model.5<-allEffects(model.5)
regr<-lm(Zn.ppm~Daydiff+Treatment+Block, data=SerumDairyCompl)
plot(allEffects(regr)) # smaller confidence intervals then multilevel model

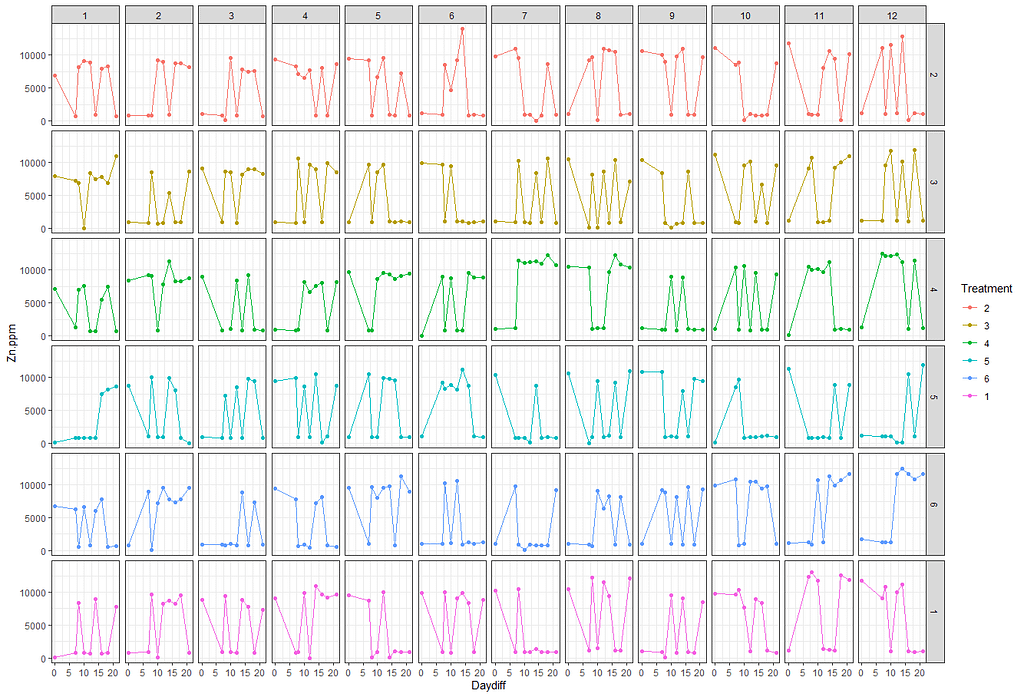
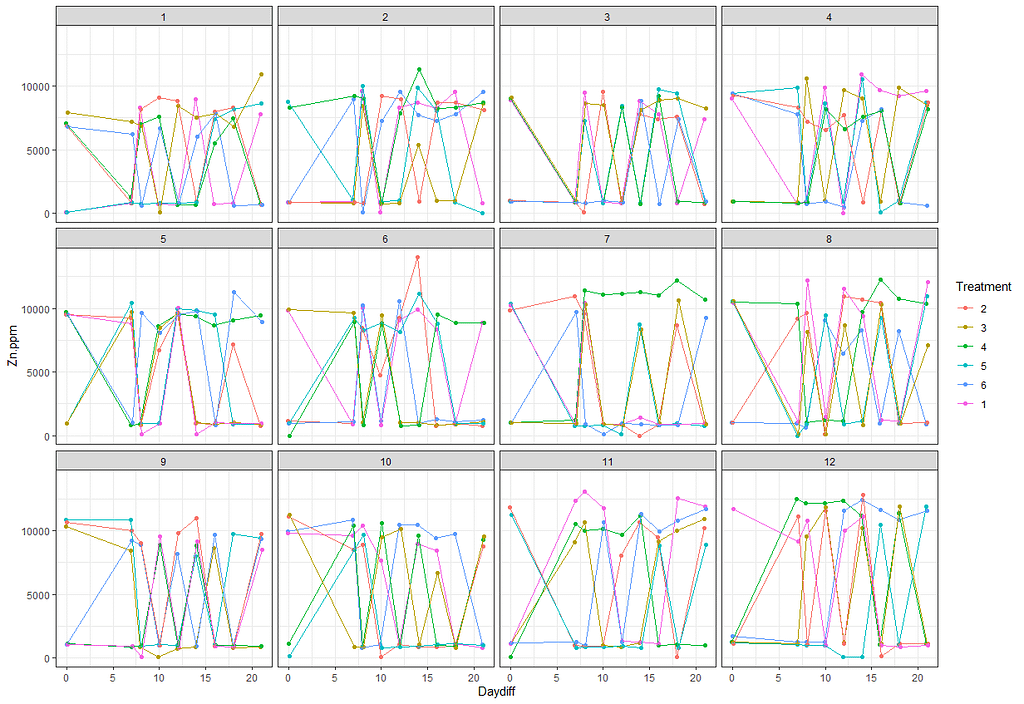
Once again, seeing these plots, the results are not really surprising.

Next up I will extend the model using the block effect.

## Adding block effect
SerumDairy$Block<-as.integer(SerumDairy$Block)
model.l<-lmer(Zn.ppm~1 + Daydiff + (1|Cow), SerumDairyCompl, REML=FALSE) # random intercept + fixed slope
model.lttb<-lmer(Zn.ppm~1 + Daydiff+Treatment++(1|Cow), SerumDairyCompl, REML=FALSE)
summary(model.lttb)
model.lttbr<-lmer(Zn.ppm~1 + Daydiff+Treatment+Block+(1|Cow) + (1|Block), SerumDairyCompl, REML=FALSE)
summary(model.lttbr)
anova(model.lttb, model.lttbr)
model.lttbri<-lmer(Zn.ppm~1 + Daydiff*Treatment*Block + (1|Block/Cow), SerumDairyCompl, REML=FALSE) # (1|Block/Cow) is the same as (1|Cow) & (1|Block)
summary(model.lttbri)
anova(model.l,model.ltt,model.lttbri)

Once again, the single model of a day difference slope and a random intercept performs best.

Then I will look for the interaction effect. At this point, I already got a feeling how a direct comparison will end up in the results.

# Interaction effects or just fixed effects?
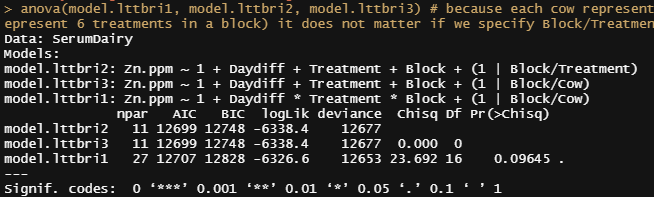
model.lttbri1<-lmer(Zn.ppm~1 + Daydiff*Treatment*Block + (1|Block/Cow), SerumDairy, REML=FALSE) # (1|Block/Cow) is the same as (1|Cow) & (1|Block)
model.lttbri2<-lmer(Zn.ppm~1 + Daydiff+Treatment+Block + (1|Block/Treatment), SerumDairy, REML=FALSE) 
model.lttbri3<-lmer(Zn.ppm~1 + Daydiff+Treatment+Block + (1|Block/Cow), SerumDairy, REML=FALSE) 
anova(model.lttbri1, model.lttbri2, model.lttbri3) # because each cow represent the treatment in a block (6 cows to represent 6 treatments in a block) it does not matter if we specify Block/Treatment or Block/CoW

Interaction effects does not add anything.

Time to compare the most likely models even deeper.


model.1<-lme4::lmer(Zn.ppm~1 + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

model.2<-lme4::lmer(Zn.ppm~Daydiff + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

model.3<-lme4::lmer(Zn.ppm~Daydiff + Treatment + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

model.4<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (1|Block), SerumDairyCompl, REML=FALSE)

model.5<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

model.6<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (Daydiff|Treatment) + (1|Block/Treatment), SerumDairyCompl, REML=FALSE) # is maximal model possible, random slopes + intercept by subjects, and random intercept of treatment, blocks and treatment within blocks. But Corr is NaN which seems like overfitting the model or making it redundant

model.7<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (0+Block|Treatment), SerumDairyCompl, REML=FALSE) # experimental model, leaving the intercept alone, and thus only specifying the random slope. Do not fully understand that model yet.

model.8<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (1|Treatment) + (1|Block), SerumDairyCompl, REML=FALSE) # shows varing intercepts by Block, not by Treatment. Is that even possible?
 
model.9<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (1|Cow), SerumDairyCompl, REML=FALSE
, SerumDairyCompl, REML=FALSE)

model.10<-lme4::lmer(Zn.ppm~Daydiff + I(Daydiff^2) + Treatment + Block + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

model.11<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (1|Block:Treatment), SerumDairyCompl, REML=FALSE)

model.11<-lme4::lmer(Zn.ppm~Daydiff + Treatment + (1|Block:Treatment), SerumDairyCompl, REML=FALSE)

model.12<-lme4::lmer(Zn.ppm~1+(1|Block:Treatment:Daydiff), SerumDairyCompl, REML=FALSE) # Error: number of levels of each grouping factor must be < number of observations

model.13<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (1|Block) + (1|Block:Treatment), SerumDairyCompl, REML=FALSE) # exact same as model.5

model.14<-lme4::lmer(Zn.ppm~Daydiff + Block + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

model.15<-lme4::lmer(Zn.ppm~Daydiff + Block + (1|Block), SerumDairyCompl, REML=FALSE)

model.16<-lme4::lmer(Zn.ppm~poly(Daydiff,3) + Treatment + Block + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

A lot of models that we can easily compare using the jtools package.

jtools::plot_summs(model.2,
                   model.3,
                   model.4, 
                   model.5,
                   model.6,
                   model.7,
                   model.8,robust = "HC3",
                   model.names = c("+Daydiff",
                                   "+Treatment",
                                   "only (1|Block)",
                                   "(1|Block/Treatment)",
                                   "(1|Daydiff/Treatment)",
                                   "(0+Block|Treatment)",
                                   "(1|Treatment) + (1|Block)"))

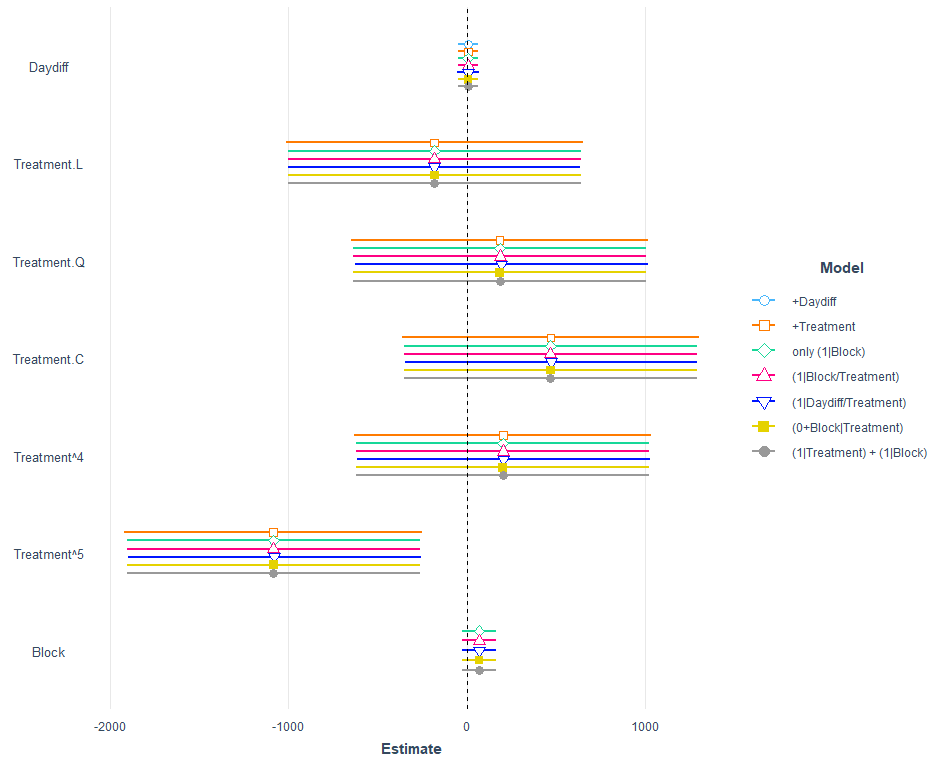
They all kind of show the same effect estimates. In that case, pick the easiest model.

Let's see how the other models perform.

jtools::plot_summs(model.10,
                   model.11,
                   model.13,
                   model.14,
                   model.15,
                   model.16,
                   robust = "HC3",
                   model.names = c("+I(Daydiff^2)",
                                   "+(1|Block:Treatment)",
                                   "(1|Block) + (1|Block:Treatment)",
                                   "(1|Block/Treatment)",
                                   "(1|Block)",
                                   "poly(Daydiff,3)"))

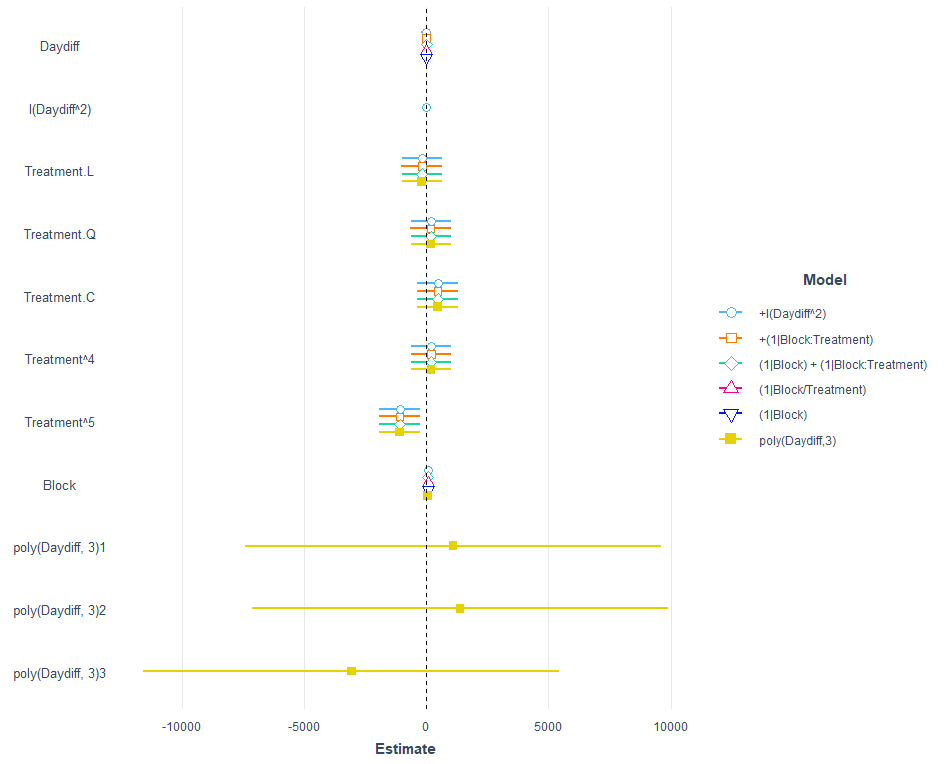
I am going to pick a model now, model.5, because it makes the most sense given the design set-up. Given the data, though, it would very well be a good idea to jus pick the simplest model showing just an effect of time.

# diagnostic plots model.5
plot(allEffects(model.11))
plot(model.11, type=c("p", "smooth"))
plot(model.11, sqrt(abs(resid(.)))~fitted(.), type=c("p", "smooth"))
qqmath(model.11, id=0.05)

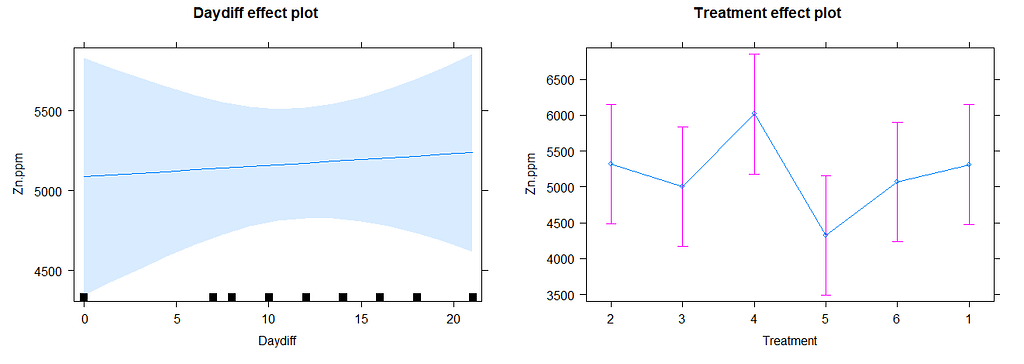
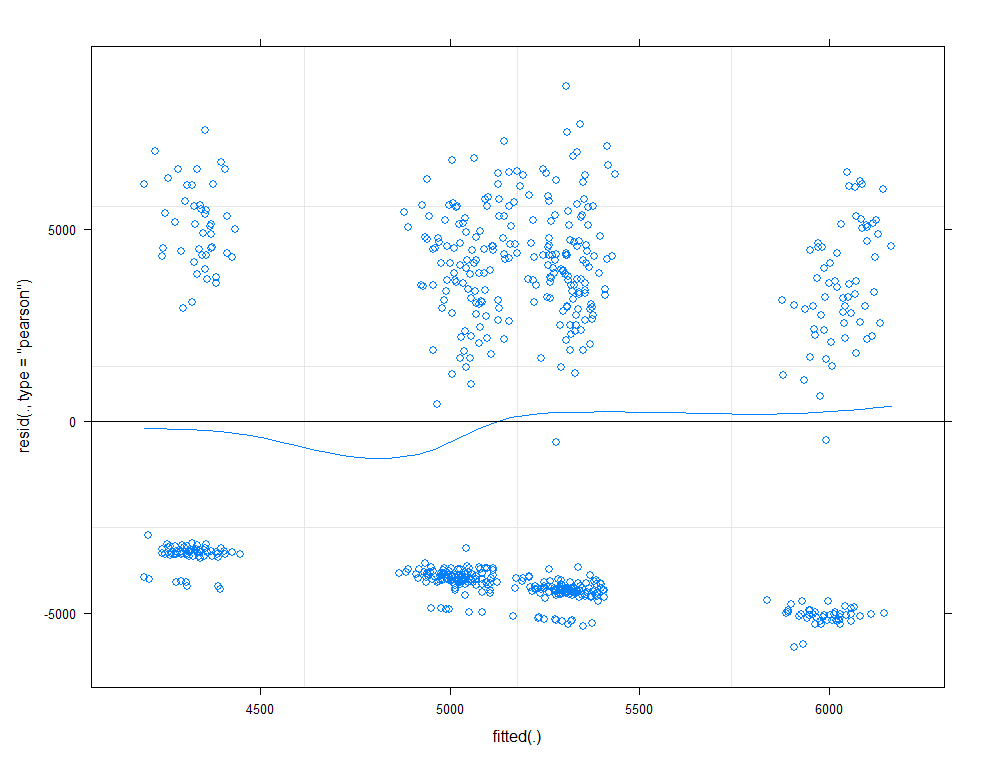
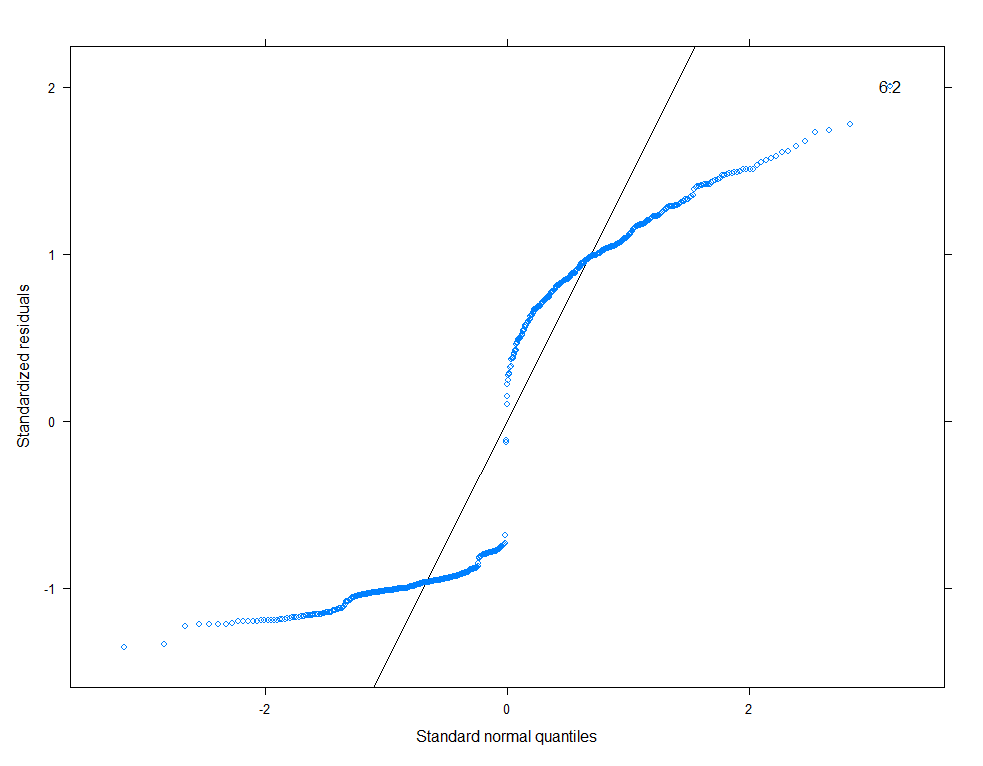
As you caan the diagnostics opf the model are not good.

There is a nice package, called HLMdiag, that will let you venture deeper into the residuals of the models do diagnostics on various levels.

model.l<-lmer(Zn.ppm~1 + Daydiff + (1|Cow), SerumDairyCompl, REML=FALSE)
model.q<-lmer(Zn.ppm~1 + Daydiff + I(Daydiff^2) + (1|Cow), SerumDairy, REML=FALSE)
model.q3<-lmer(Zn.ppm~1 + Daydiff + I(Daydiff^2) + I(Daydiff^3) + (1|Cow), SerumDairy, REML=FALSE) # cubic model
model.qr<-lmer(Zn.ppm~1 + Daydiff + I(Daydiff^2) + (Daydiff|Cow), SerumDairy, REML=FALSE)

model.l.resid <- hlm_resid(model.l, standardize = TRUE, include.ls = TRUE, level=1)
ggplot(data = model.l.resid, aes(x = Daydiff, y = .std.ls.resid)) + 
  geom_point(alpha = 0.2) +
  geom_smooth(method = "loess", se = FALSE) + 
  labs(y = "LS level-1 residuals", title = "LS residuals against Day Difference")

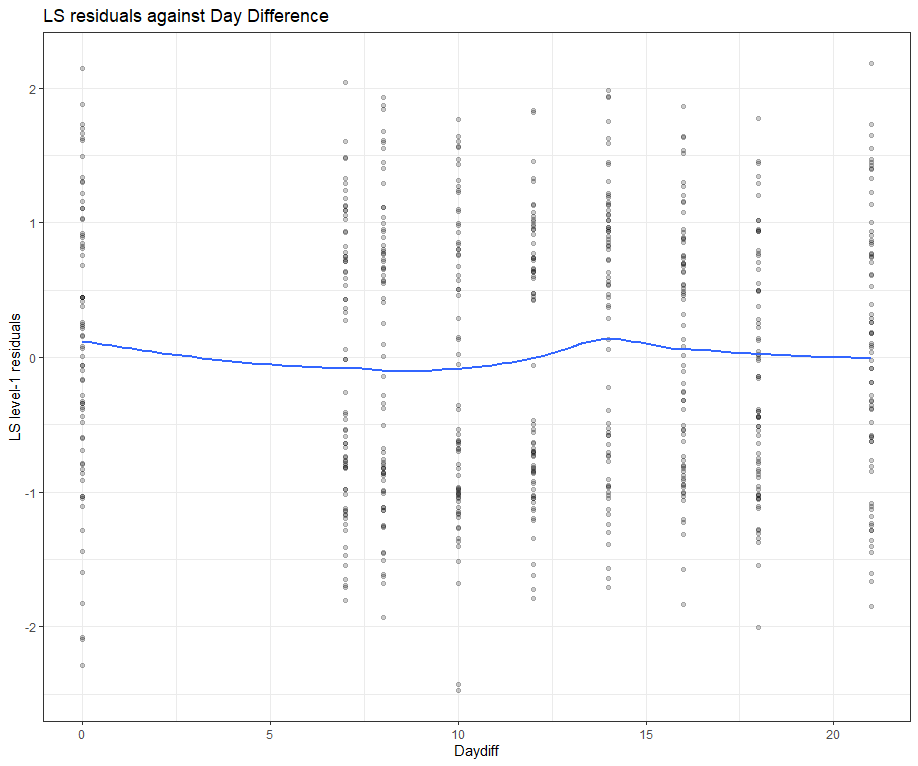
The residuals of the most straightforward model, which look good to me.

Then, I want to look at influencers and will do so by looking at the first level of the data, which is the observation. Below you can see that there are for sure some influential observations, but that does not mean that they require deletion. When you find influencers or outliers, they show you a hint for real-life mechanisms. You should cherish them if you find them. If the model cannot handle them, the model shows its limitations.

All of the above is applicable when the observations labeled outliers are not BAD data. They should not be mistakes.

model.l.infl  <- hlm_influence(model.l, level = 1)
dotplot_diag(model.l.infl$cooksd, name = "cooks.distance", cutoff = "internal")
dotplot_diag(model.l.infl$cooksd, name = "mdffits", cutoff = "internal")
dotplot_diag(model.l.infl$cooksd, name = "covratio", cutoff = "internal")
dotplot_diag(model.l.infl$cooksd, name = "rvc", cutoff = "internal")

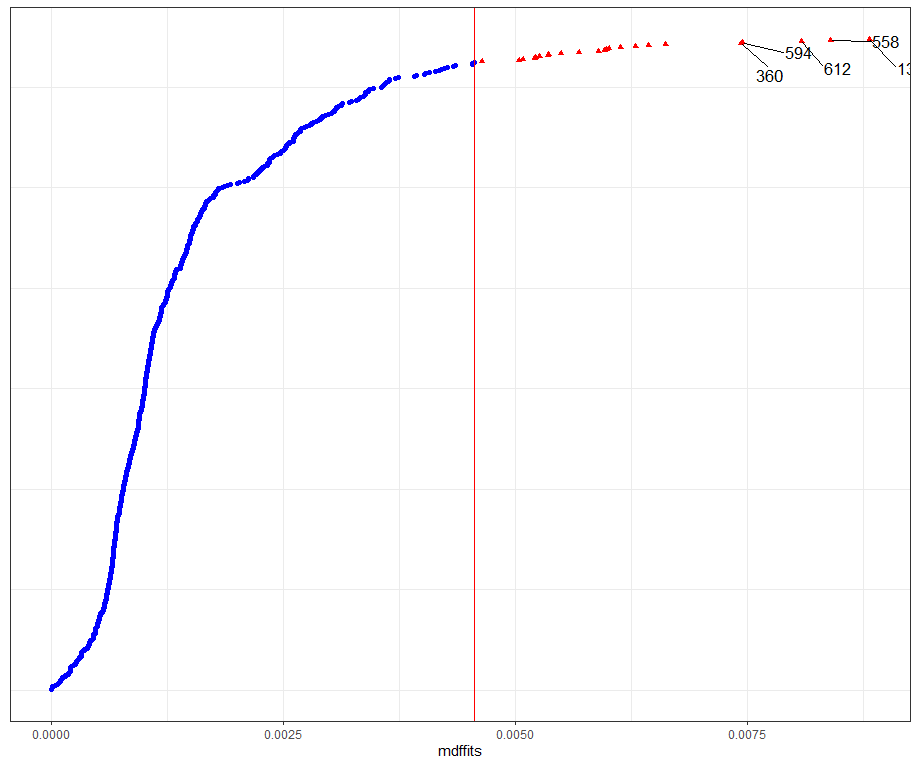
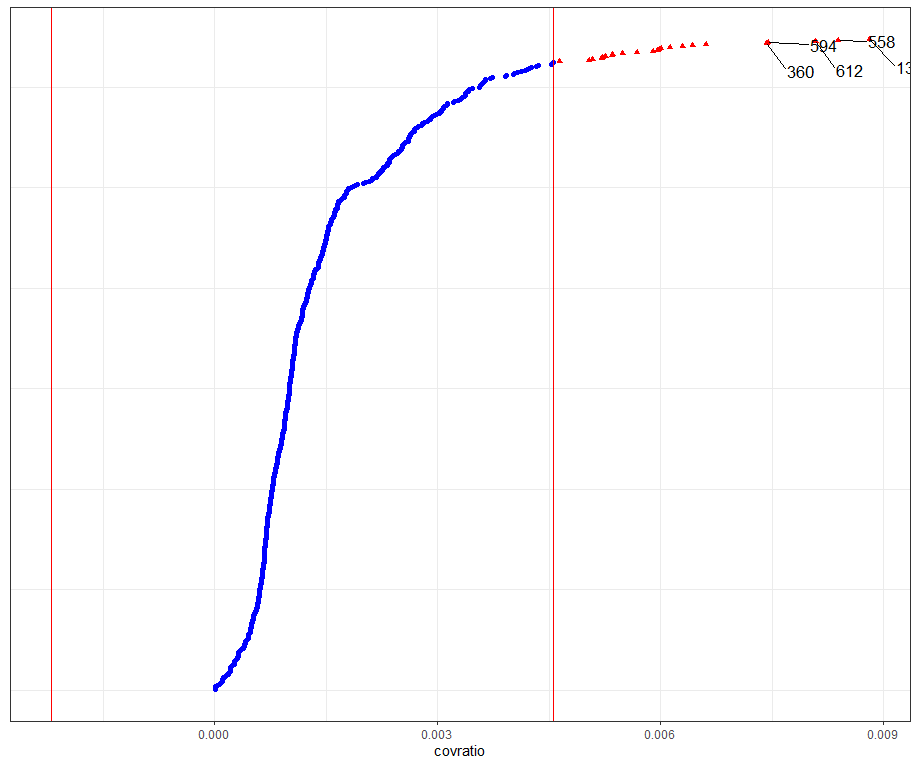
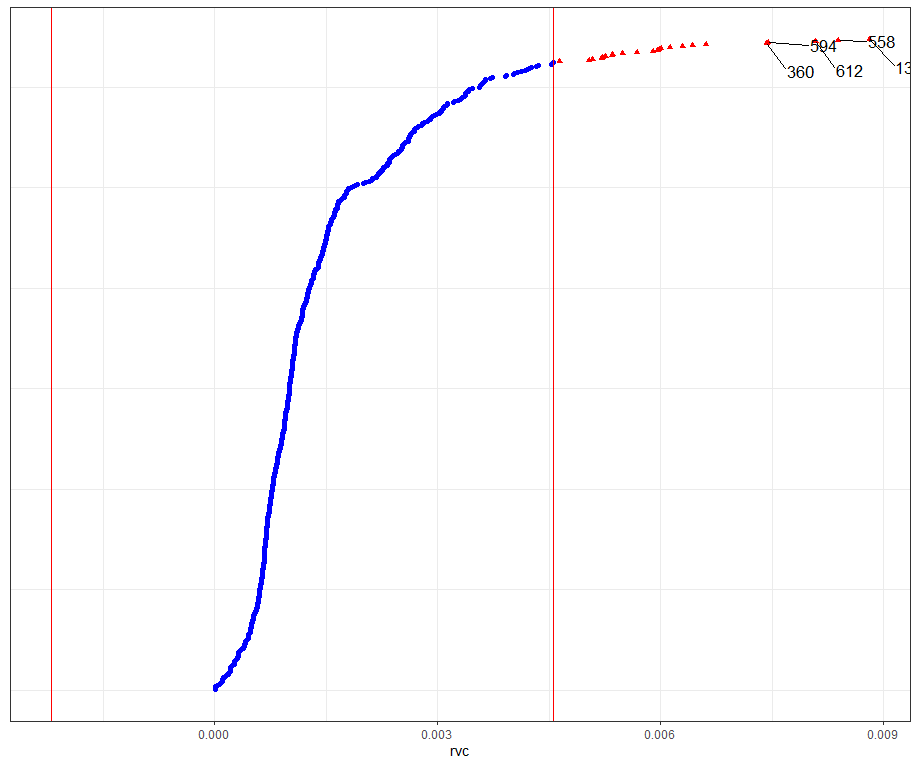
What if I start deleting cows entirely?

model.l.del<-case_delete(model.l, level="Cow", type="both")
model.l.del$fitted.delete<-as.data.frame( model.l.del$fitted.delete)
ggplot(data = model.l.del$fitted.delete, 
       aes(y = as.factor(deleted), 
           x= as.factor(Daydiff), 
           fill=fitted.x.)) + 
  geom_tile() +
  scale_fill_viridis_c(option="C")+
  theme_bw()+
  labs(y = "Deleted cow",
       x = "Day difference", 
       title = "Changes in Zn (ppm) by deletion of cows")

Not really a change. Once again, I would have expected this anyhow if you look at the earliest plots. There is variance all over the dataset.

Next up I want to take a look at the posterior predictive simulations coming from model 5. First, let's fit model 5.

model.5<-lme4::lmer(Zn.ppm~Daydiff + Treatment + Block + (1|Block/Treatment), SerumDairyCompl, REML=FALSE)

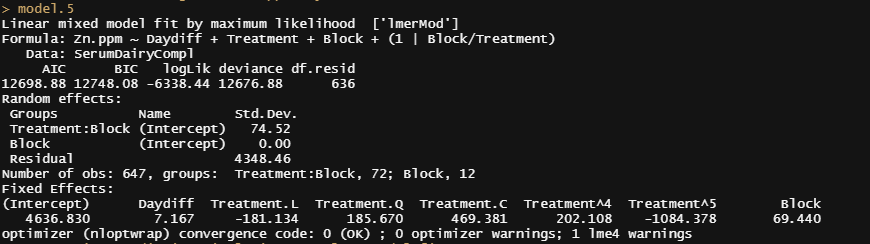
All looks well, except that the block variance does not do a single thing it seems.

Then the simulation work begins.

mySumm <- function(.) { s <- sigma(.)
c(beta =getME(., "beta"), sigma = s, sig01 = unname(s * getME(., "theta"))) }
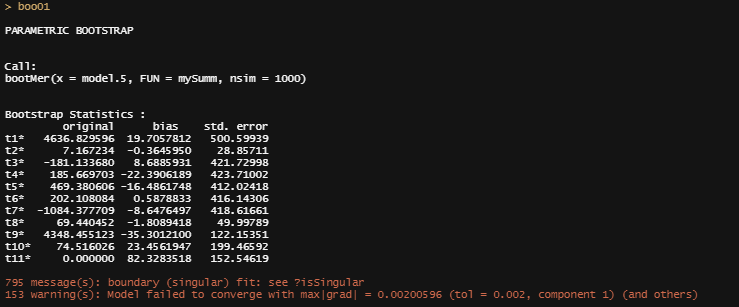
boo01<-bootMer(model.5, mySumm, nsim = 1000)
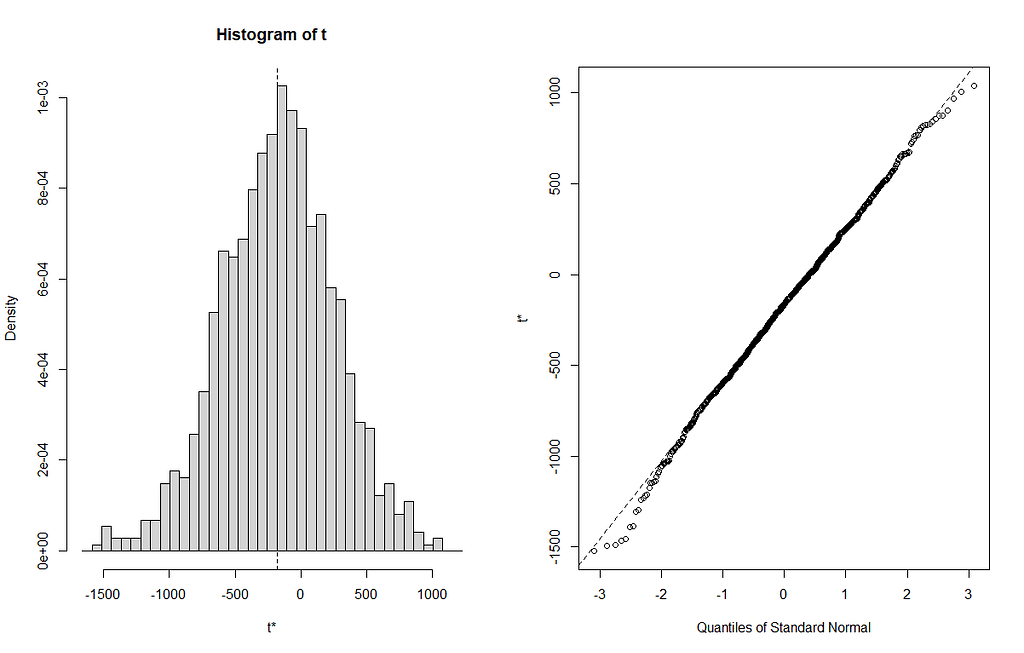
plot(boo01,index=3)

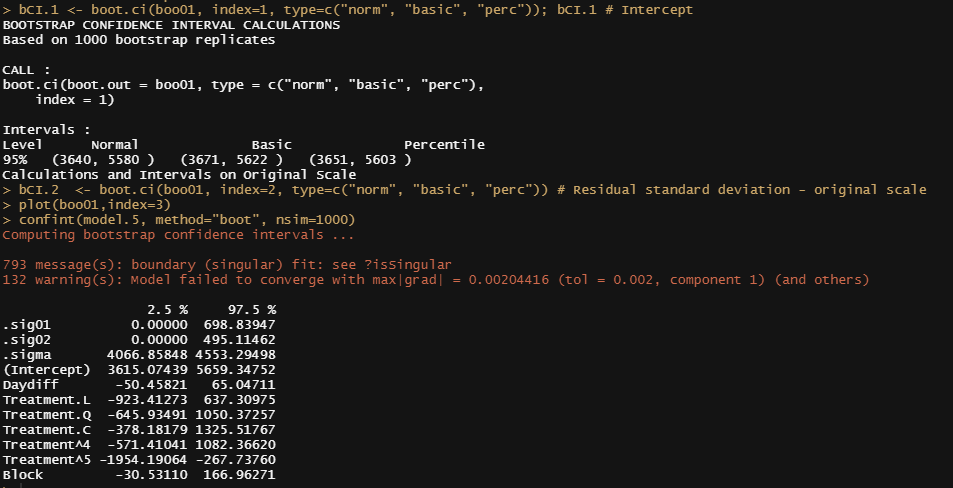
Here, you can see the values coming from the bootstrap. These 11 values represent the 11 variables measured in **model.5.** What you are looking for in such a simulation is not significant, but spread. How big is the bias and how big is the standard error? Large numbers hint at unstable datasets.

From the bootstrapped results I can extract particular kinds of confidence intervals at various levels, and plot them. Here, you see the distribution via a histogram and the qq-plot of the 3rd variable, t3. It coincides with Treatment.L. Hence, it shows the effect of Treatment.L compared to the reference treatment via resampling. The resampling shows what you want it to show — normal distribution like spread. For Treatment.L however, the no-effect now becomes blatantly clear.

From all of this, we can choose which kind of confidence to choose. They are not all the same. From the function, you can choose:

Normal. A matrix of intervals is calculated using the normal approximation. It will have 3 columns, the first being the level and the other two being the upper and lower endpoints of the intervals.
Basic. The intervals were calculated using the basic bootstrap method.
Student. The intervals were calculated using the studentized bootstrap method.
Percent. The intervals were calculated using the bootstrap percentile method.
BCA. The intervals were calculated using the adjusted bootstrap percentile (BCa) method.

## ------ Bootstrap-based confidence intervals ------------
bCI.1 <- boot.ci(boo01, index=1, type=c("norm", "basic", "perc")); bCI.1 # Intercept
bCI.2  <- boot.ci(boo01, index=2, type=c("norm", "basic", "perc")) # Residual standard deviation - original scale
plot(boo01,index=3)
confint(model.5, method="boot", nsim=1000)

I am requesting the normal, basic, and percent confidence intervals for t1. As you can see they differ.

Like I said before, R has a way of doing the same thing in many different ways via different packages. Below I show the prediction intervals coming from the merTools package and the lme4 bootMer function.


PI<-predictInterval(model.5, newdata=SerumDairyCompl, level=0.95, n.sims=1000, stat="median", type="linear.prediction", include.resid.var=T)
head(PI)

ggplot(aes(x=1:30, y=fit, ymin=lwr, ymax=upr), data=PI[1:30,])+geom_point()+geom_linerange()+labs(x="Index", y="Prediction w/95% PI") + theme_bw()

The linear prediction of the model via bootstrapping, hsowing the first 30 extractions

mySumm <- function(.) {
        predict(., newdata=SerumDairyCompl, re.form=NULL)
}

####Collapse bootstrap into median, 95% PI
sumBoot <- function(merBoot) {
        return(
                data.frame(fit = apply(merBoot$t, 2, function(x) as.numeric(quantile(x, probs=.5, na.rm=TRUE))),
                           lwr = apply(merBoot$t, 2, function(x) as.numeric(quantile(x, probs=.025, na.rm=TRUE))),
                           upr = apply(merBoot$t, 2, function(x) as.numeric(quantile(x, probs=.975, na.rm=TRUE)))))}

boot1 <- lme4::bootMer(model.5, mySumm, nsim=1000, use.u=FALSE, type="parametric")
PI.boot1 <- sumBoot(boot1)
ggplot(PI.boot1)+
  geom_density(aes(x=fit))+
  geom_density(aes(x=lwr, fill="red"),alpha=0.5)+
  geom_density(aes(x=upr, fill="red"),alpha=0.5)+
  theme_bw()+
  theme(legend.position = "none")

Now you can see them all — the fitted and lower and upper confidence intervals as distributions of themselves with places for overlap. The plot may look a bit strange but I am really interested in spread here. How good is my model performing?

What I will be doing is now is going back a little bit, looking at the interactions. I want to figure out what happened, and I will use the ANOVA models to take a closer look. Since the data is balanced, ANOVA will work just fine. Otherwise, I would have to use mixed models.

model.5.aov<-aov(Zn.ppm~Daydiff+Treatment*Block, data=SerumDairyCompl)
coef(model.5.aov)
summary(model.5.aov)
par(mfrow=c(2,1))
interaction.plot(SerumDairyCompl$Daydiff, SerumDairyCompl$Block, SerumDairyCompl$Zn.ppm, col=seq(1,12,1))
interaction.plot(SerumDairyCompl$Daydiff, SerumDairyCompl$Treatment, SerumDairyCompl$Zn.ppm, col=seq(1,6,1))

It looks like there is room for interaction, but these effects are truly day effects. Which is what every model keeps showing.

rr<-ranef(model.5)
dotplot(ranef(model.5, condVar=T))
qqmath(ranef(model.5)); abline(0,1)

Assessment of the random effects of the model. It is safe to say that it is good to not include any random effects. You would expect diverging lines, not similar mean values, and insane confidence intervals.

You can also use bootstrapping to compare models. Labour intensive for the pc so makes sure you run in parallel.

# parametric bootstrapping of confidence values when comparing models
(nc <- detectCores())
cl <- makeCluster(rep("localhost", nc))
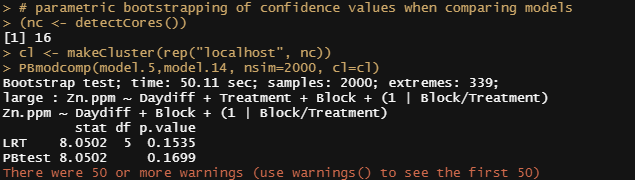
PBmodcomp(model.5,model.14, nsim=2000, cl=cl)

Let's look further at the models, using the MerTools package again. Via MerTools you simulate values of the fixed effects from the posterior using te function arm::sim. FEsim is a convenience wrapper to do this and provides an informative dataframe.

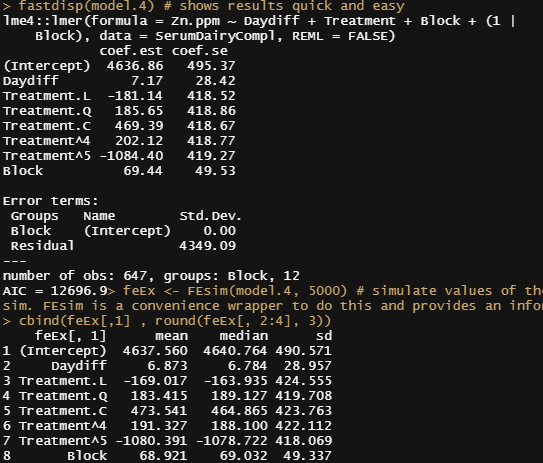
fastdisp(model.4) 
feEx <- FEsim(model.4, 5000) # simulate values of the fixed effects from the posterior using te function arm::sim. FEsim is a convenience wrapper to do this and provides an informative dataframe
cbind(feEx[,1] , round(feEx[, 2:4], 3))
library(ggplot2)
plotFEsim(feEx) + 
        theme_bw() + 
        labs(title = "Coefficient Plot of InstEval Model", x = "Median Effect Estimate", y = "Evaluation Rating") # The lighter bars represent grouping levels that are not distinguishable from 0 in the data.
reEx <- REsim(model.5, 5000); reEx
table(reEx$groupFctr)
table(reEx$term)
lattice::dotplot(ranef(model.5, condVar=TRUE))
p1 <- plotREsim(reEx); p1

Shows only a single treatment effect, and absolutely no need for random effects. Which we already knew.

plot(model.4)
plot_model(model.4, type="diag")

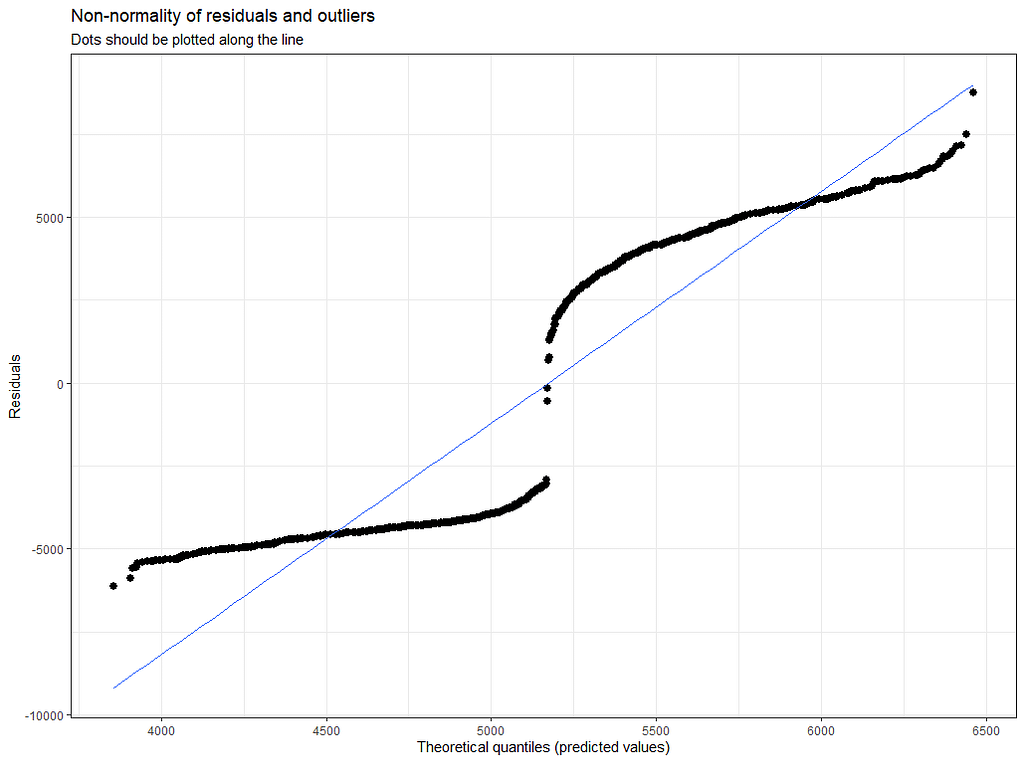
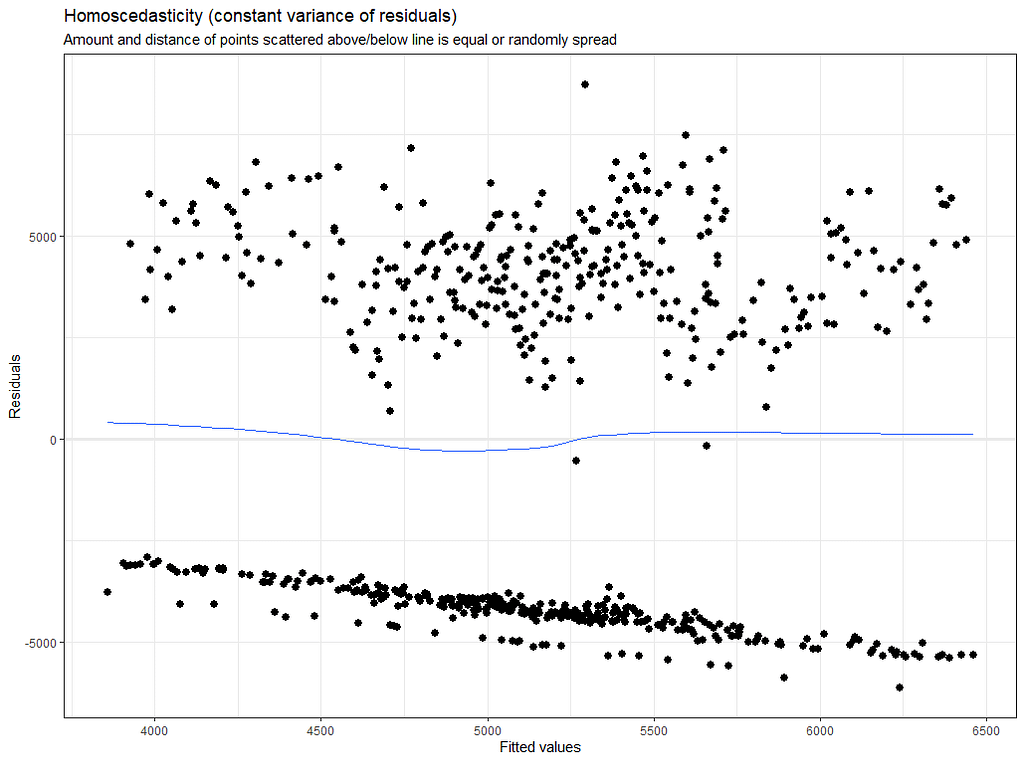
Last but not least, predicted vs observed to see model fit.

SerumDairyFitted<-broom.mixed::augment(model.4)
ggplot(SerumDairyFitted, aes(x=Zn.ppm, y=.fitted, colour=.resid, size=Block))+
  geom_point()+
  geom_abline(slope=1, lty=2)+
  scale_color_viridis_c(option="C")+
  facet_wrap(~Treatment, scales="free")+
  labs(title="Fitted vs Observed from Mixed Model 4",
       x="Observed Zn (ppm)",
       y="Predicted Zn (ppm)")+
  theme_bw()

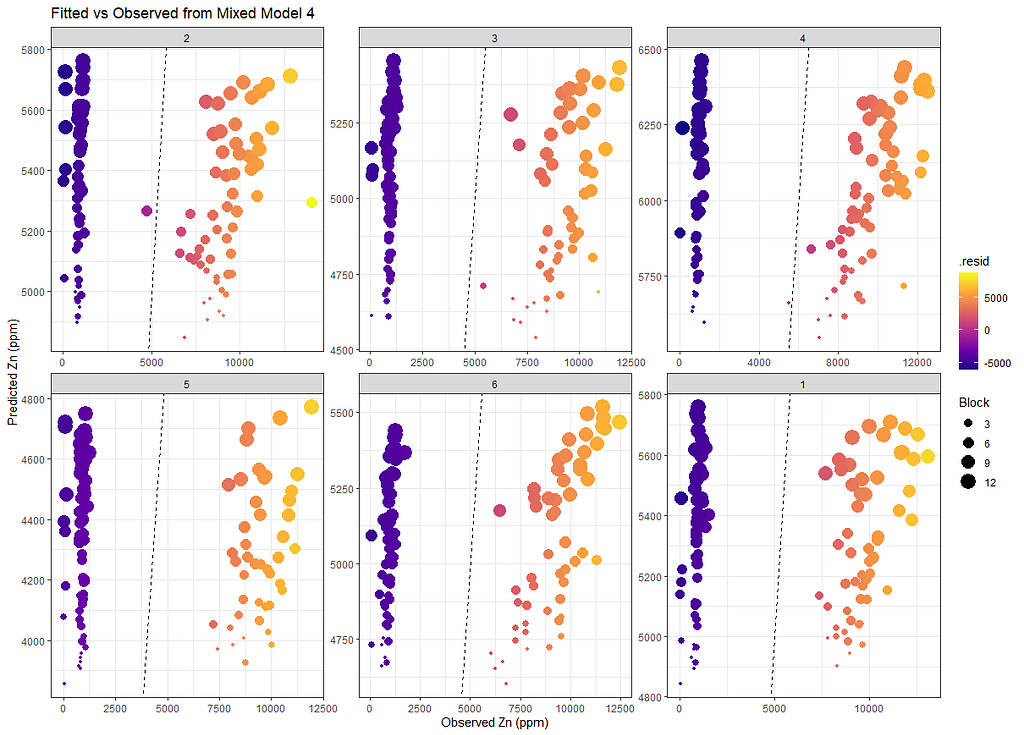
Sometimes, it is best to leave the data for what it is and do not model it. We already saw this from the graphs alone, but back then I could nog give it a rest. It is commercial data anyhow.

Don't make my mistakes!

Serum analysis was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI

Frequently Used, Contextual References

Resources

Publication

Author(s): Dr. Marc Jacobs

Data Analysis

Hunting for a mixed model in R

Towards AI Team

Feedback ↓ Cancel reply

Popular posts

Best Laptops for Deep Learning, Machine Learning (ML), and Data Science for 2023

Best Workstations for Deep Learning, Data Science, and Machine Learning (ML) for 2022

Descriptive Statistics for Data-driven Decision Making with Python

Best Machine Learning (ML) Books - Free and Paid - Editorial Recommendations for 2022

Best Data Science Books - Free and Paid - Editorial Recommendations for 2022

Updates

Recent Posts

Your Data is the New Currency: Are You Protecting It?

AI Agent Software: The Future of Coding Tools

Architecting Intelligent Multi-Agent AI Systems: A2A vs MCP

I Built an AI That Turns Side Projects Into Stories That Get You Hired

🧠 Building an AI Study Buddy: A Practical Guide to Developing a Simple Learning Companion

The World’s Leading AI and Technology Publication.

Company

CONTACT US

🔥 Recommended Articles 🔥

Cookie	Duration	Description
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.

Frequently Used, Contextual References

Resources

Publication

Serum analysis

Author(s): Dr. Marc Jacobs

Hunting for a mixed model in R

Towards AI Team

Related posts

Feedback ↓ Cancel reply

Popular posts

Updates

Recent Posts

The World’s Leading AI and Technology Publication.

Company

CONTACT US

GDPR CCPA Statement

Subscribe to our AI newsletter!

🔥 Recommended Articles 🔥