Manager, use this to plan the smart working days for your team!

Author(s): Alberto Prospero

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Optimization

A mathematical optimization tool to schedule smart working days and plan returns to the office

Introduction

During covid-19 several teams were constrained to work from home entirely. Fortunately, the situation has partially improved during the last year and in many countries, teams are being allowed to partially return to the office. This project aims to provide a tool to all managers for better planning the return of employees to the office or the smart working days for the next weeks.

The article is organized as it follows:

• Motivation, expressing the reasons why an optimization algorithm can help in planning and scheduling.
• Optimization algorithm, providing an introduction to the main objects of the mathematical optimization.
• Modeling, detailing how part of the optimization modeling was performed. This is the most challenging section and can be skipped.
• Results, describing the results obtained from the algorithm.
• Conclusion, wrapping up.

In the article, I assume that you have some familiarity with concepts and ideas related to mathematical optimization. If this is not the case, I recommend having a look at this free course on Coursera. It is tough, but it is worth it!

You can find all the details and the code on my GitHub page.

Motivation

Planning the return of employees to the office can be a complicated task for humans. Choosing the best possible configuration can be incredibly challenging, especially if there are many constraints to take into account. For example, we might need to consider the return preferences of the employees, the available workstations, the maximum capacities of rooms, and social distances. Considering all of these at the same time might be hard for humans, especially if we are aiming to find the best possible configuration.

For these reasons, an optimization algorithm can help. It can take into account different factors, define hard constraints to prevent specified configurations, and mathematically be sure that the identified solution is the optimal one.

Optimization parameters

The optimization model is composed of three main objects: the decision variables, the objective function, and the constraints. Any of these can be fully customized within the code.

The decision variables
Each decision variable is a binary variable xᵢⱼ which represents whether the employee i comes back to the office on day j.

The objective function
The objective function is composed of different terms. Notice the weight assigned to each of these can be customized within the code so that terms can be excluded from the optimization process.

• Consecutive days. For an employee might be easier to come back on consecutive weekdays, so whenever this occurs the objective function is increased.
• Same team. Members of the same team prefer to come back on the same days, so whenever this occurs the objective function is increased.
• Target presence. Every employee should come back a minimum number of days, encouraging some equity in the returns to the office. So, whenever an employee does not reach a provided mean presence across the planning period, a penalty is added to the objective function.
• Single returns. Returns to the office should be encouraged, so whenever there is a presence in the office of any employee on any day the objective function is increased.

The constraints
We have two types of constraints:

• Maximum and minimum number of employees. There is a maximum and a minimum number of employees who can return to the office per day. The optimization algorithm prevents finding solutions that exceed these values.
• Preference days. The employees are allowed to choose what days they can and can not come back. The optimization algorithm finds solutions that agree with these preferences.

Modeling

To solve the optimization problem we need to express each element of the constraints and of the objective function in terms of the decision variables.

Since we are using binary variables, we are very flexible on what we can express. Assume we are trying to express the term consecutive days, which aims to promote the returns of employees on consecutive days.

Recall that each decision variable xᵢⱼ represents whether employee i comes to the office on day j. Now, let us focus on a single employee, and consider the related sequence x₁, x₂, .., xⱼ, …, xₙ of decision variables, where n is the number of days in the planning period.

If we considered n = 2 (i.e. we are planning for 2 days), then we would like to find a function 𝑓 of x₁, x₂ such that it is zero when x₁ = 0 or x₂ = 1 and one when x₁ = 1 and x₂ = 1:

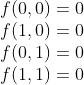
In so doing, when the employee comes to the office both on day 1 and day 2 (i.e. when x₁ =1 and x₂= 1) the consecutive-days term is 1 and the objective function is increased by 1. Instead, when this is not true, the term is 0 and the objective function is not increased.

Such a function 𝑓 can be easily expressed as:

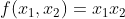
Now, assume n = 3 (i.e. planning for 3 days). Similarly, we would like to find a function 𝑓 of x₁, x₂, x₃ such that it is 2 when x₁ = 1, x₂ = 1 and x₃ = 1 (i.e. the employee comes back for all the three days), it is 1 when x₁ = 1 and x₂ = 1 or x₂ = 1 and x₃ = 1 (i.e. the employee comes back on the first day and on the second day or on the second day and on the third day), and it is 0 otherwise:

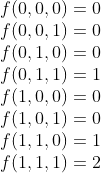
Such a function is an extension of the previous case, and can be expressed as:

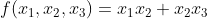
You can see the pattern. In general, for n days, the consecutive-days term can be expressed as:

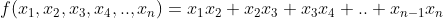
Linearization

There is one side note. You might have noticed that the derived term is not a linear term. When added to the objective function, it causes this to be non-linear, and in turn, this gives rise to some issues in finding the optimal solution. In fact, linear problems are guaranteed to mathematically find a unique and optimal solution. Also, almost all (free) solvers work just in the case of linear optimizations.

However, we can use an interesting strategy to make the terms linear, in the case of binary product decision variables. Specifically, for each binary product, we introduce a new binary variable z = xᵢ * xⱼ (where in this case xᵢ and xⱼ are two binary variables), and a set of constraints on z, which are given by:

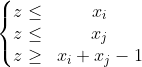
The variable z behaves as the binary product. When xᵢ = 0 or xⱼ = 0, z needs to be smaller than 0 and so it has to be zero. When xᵢ = 1 or xⱼ = 1, z needs to be greater than 1 and so it has to be one. Hence, we can lead back to the linear case.

Finally, notice that a similar process has to be repeated for each term of the objective function and of the constraints, in order to be able to specify the whole optimization problem.

Results

To run the code and get the results, we focused on a particular initial configuration, but it can be fully customized to adapt to your needs. In this scenario, we are going to assume the following setting:

• The number of employees is 13 (named as Italian foods 🙂 )
• There are 20 days (corresponding to 4 weeks, i.e. 1 month) to plan
• 4 minimum employees are allowed to return to the office on the same day. 6 maximum employees are allowed to return to the office on the same day.
• 8 days during the planning period (i.e. 2 days per week) is the target presence that every employee should reach or exceed.
• There are 4 employee sub-teams, defined as follows:
  – Employees number 1,2 3
  – Employees number 4,5,6
  – Employees number 8, 9, 10
  – Employees number 11, 12
  Note that one employee might be part of more sub-teams.

Finally, the employee preferences are reported below. Cells in light green represent the days when employees can not come back to the office and have to be avoided in the optimization solution. Cells in dark green represent the days when employees can come back to the office.

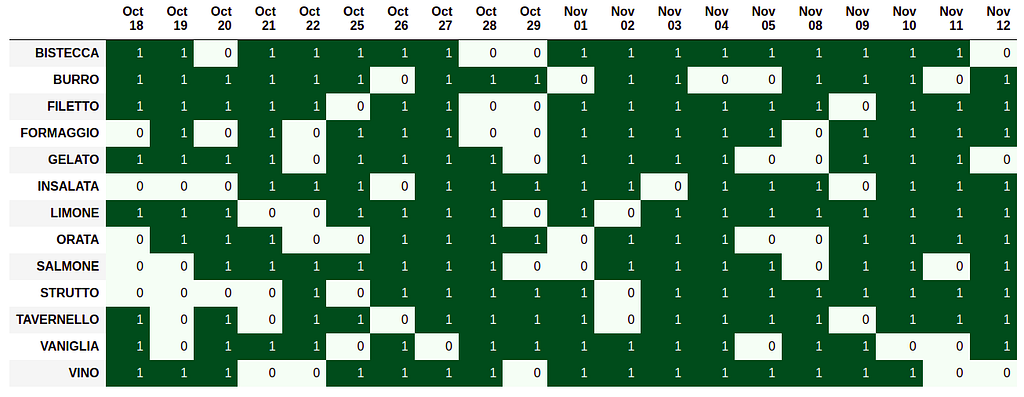
Now, it is time to run our Python notebook and get the results:

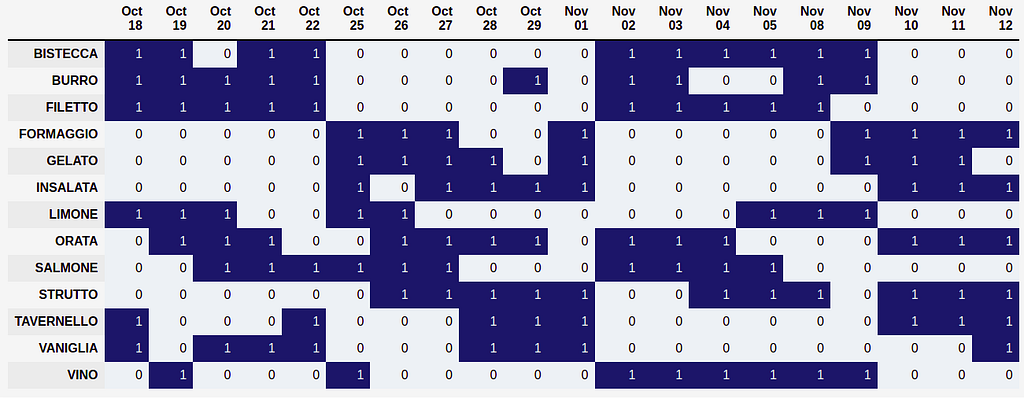
As you can see, the algorithm made tremendous work! The clusters formed by employees of the same sub-teams are clear in the plot, and employees do tend to come to the office on consecutive days. Also, notice that the number of employees on each day does not exceed the prescribed limits, and every employee comes back at least 8 days during the planned period!

Wow! Loving math!

Conclusions

In this article, we described a tool that allows identifying the best planning for teams returning to the office or in smart working. It is built using a mathematical algorithm taking into account different constraints and factors at the same time. We set up an initial configuration and showed the benefits of using such an algorithm.

Notice that there is a number of improvements that can be made to the algorithm, which ultimately depend on personal requirements and needs. For example, we might want that the presence of employees or teams would be more uniform across the planned period, or that some employees are not encouraged in returning on consecutive days.

Nevertheless, the use of such a tool can be extremely powerful in saving time and resources to managers needing to plan returns to offices or smart-working days for their teams.

Hope you enjoyed the post, please feel free to comment and give a thumbs up!
Stay gold!

---

Manager, use this to plan the smart working days for your team! was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI