DoRA Explained: Next Evolution of LoRA?

Author(s): Youssef Farag

Originally published on Towards AI.

Paper link: https://arxiv.org/abs/2402.09353

Code: https://github.com/NVlabs/DoRA

Released: 14th of February 2024

No one can deny how crucial Low-Rank Optimization (LoRA)[2] is for fine-tuning LLMs. It has become the primary solution for managing fine-tuning with limited hardware. LoRA, along with its quantized version (QLoRA)[3], has been dominating the field of fine-tuning since its release by Microsoft back in 2021.

Although LoRA and QLoRA remain widely used today due to their convenience and speed, they still fall short of full finetuning of LLMs. Several studies have attempted to address this gap [4,5], and one approach in particular stands out in my opinion.

Weight Decomposed Low-Rank Adaptation (or DoRA, for short)[1] has gained significant traction with its simple yet effective method of enhancing LoRA’s performance and narrowing the gap between partial and full finetuning. In this section, we will cover the most important key points of DoRA, explore why it stands out, and take a deeper look into its approach to solving this challenge.

DoRA [1], introduced in February 2024 by Liu et al., contributes to three main points:

1. Analyzing LoRA vs. full fine-tuning: By decomposing the weight matrix into magnitude and direction, the authors highlight key differences between LoRA and full fine-tuning.
2. Decoupled optimization of magnitude and direction: DoRA optimizes magnitude and direction separately, achieving results closer to full fine-tuning while retaining LoRA’s low resource requirements.
3. Extensive evaluation and combinations with other methods: DoRA is compared to LoRA across multiple tasks, and its integration with methods like VeRA and QLoRA is explored further.

Matrix Decomposition:

To understand DoRA, it is helpful first to briefly go over vector and matrix decomposition.

Fundamentally, DoRA is built on norm-based decomposition, which denotes that any vector can be separated into its magnitude and directional components. Magnitude is a scalar indicating the vector’s length, and direction indicating its orientation in space.

Where ||v|| is the scalar norm, and v^ is the directional unit vector

Similarly, we can also decompose a matrix A as such:

||A|| measures the magnitude/ size of a matrix, and A hat is a normalized matrix retaining the directional structure.

In the context of neural networks, this can be applied to our weight matrix W as such :

This decomposition allows us to separate scale from structure, further enabling us to understand more information and patterns about our training process. DoRA also, as we will later on cover, leverages this separation to train each component separately, allowing for better optimization and more efficient parameter adaptation.

LoRA vs Full FT:

Theoretically, if we have two models, M1​ and M2​, trained using two different approaches, producing weight matrices W1​ and W2. If these weight matrices exhibit different behaviors in how their scale and direction evolve during training, this would suggest that M1​ and M2 are inherently different in their learning processes.

This is exactly what the authors demonstrate by analyzing the differences between training with LoRA and full fine-tuning. By periodically examining the relationship between magnitude and direction throughout training, they observe distinct patterns: full fine-tuning shows a negative slope (an inverse relationship between magnitude and direction), while LoRA exhibits a positive slope (a direct proportionality). (As shown in Figure 1.)

In this paper, the authors also argue that it is natural for full fine-tuning to exhibit a negative slope, since the pre-trained model weights already contain extensive knowledge relevant to downstream tasks. As a result, significant changes in either magnitude or direction alone are often sufficient for effective adaptation. This is precisely what DoRA achieves as well (as shown in Figure 1), demonstrating behavior that more closely resembles full fine-tuning than LoRA.

DoRA, Simplified

Building on their earlier analysis of weight composition, the authors propose a novel approach that trains the magnitude and directional components of the weight matrix separately. Since the directional component remains relatively large, it can be optimized using the same method as LoRA, while the magnitude vector is trained independently. Because the magnitude vector is one-dimensional (1 x k, as we will discuss shortly), this approach increases the number of trainable parameters by only about 0.01% compared to LoRA.

The weight matrix of the pre-trained LLM can be decomposed as such :

where M is the magnitude vector, V is the directional matrix, and ||V||c is the vector-wise normalization. The training formula can be extended to encapsulate the new training matrix, using the pre-trained weight matrix W0 as such:

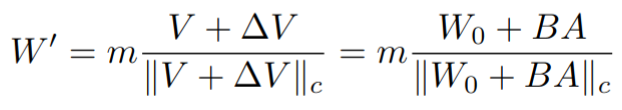
The new weight matrix after fine-tuning (W’) can be calculated by expanding V’ into two components: V (The frozen pre-trained directional component), and ∆V (The possible directional change post fine-tuning). ∆V can further be decomposed into two matrices, B and A. This follows LoRA [1], where the full fine-tuning matrix ∆V can be factorized into two simpler training matrices.

This decomposition leads to a smaller optimization target, controlled by the hyperparameter r. The smaller the rank, the smaller the fine-tuning matrix. This leads to faster training, but weaker learning ability.

Upon periodically calculating the magnitude and direction for DoRA during training, a negative correlation between magnitude and slope is observed (As seen in Figure 1), resembling the behavior of full fine-tuning. This suggests that DoRA indeed behaves more like full fine-tuning, supporting the authors’ argument that a substantial change in either magnitude or direction alone can be sufficient for effective adaptation.

Results & Key Findings:

When evaluated on 8 different reasoning datasets using 4 backbone models, DoRA consistently outperformed LoRA across all tasks. Notably, even with half the rank size (DoRA†) and therefore using half the number of trainable parameters, DoRA maintained its performance advantage over LoRA. Table 1 presents a condensed summary of these results, alongside the reported performance of ChatGPT 3.5 from the paper. On average, DoRA achieves accuracy levels that are close to, and in some cases exceed, those of ChatGPT 3.5. Note that the minor 0.01 increase in the params % of DoRA and LoRA is due to the new magnitude vector mentioned above.

One issue that [1] also discussed regarding LoRA is its sensitivity to the chosen rank during training. This requires careful tuning of the rank hyperparameter. When analyzing the performance of DoRA and LoRA across different rank sizes (seen in Figure 2), DoRA demonstrated greater stability with respect to rank variation. Furthermore, DoRA significantly outperforms LoRA at lower ranks, achieving a 22.4% and 37.2% improvement with ranks 4 and 8, respectively. This suggests that when reducing the number of trainable parameters is necessary, DoRA offers a superior alternative due to its robustness and effectiveness at lower ranks.

QDoRA and DVoRA:

All of this makes a strong case for DoRA, demonstrating its superiority over LoRA both in terms of accuracy and its closer alignment with full fine-tuning behavior. But a question still remains: how does DoRA perform when compared to more recent methods?

QLoRA and VeRA [3,4]are two novel methods recently starting to be more widely used for fine-tuning, offering even lighter weights and better performance than basic LoRA.

• QLoRA: Works by freezing and quantizing the pretrained model to 4 bits, and applying LoRA on top of the frozen model. By significantly reducing the number of trainable parameters, QLoRA enables more manageable training, particularly effective when fine-tuning huge models.
• VeRA: This method proposes freezing randomly selected low-rank matrices that are shared across various layers. As a result, it often requires even fewer trainable parameters than QLoRA for fine-tuning.

Although DoRA achieves higher accuracy than both VeRA and QLoRA (as shown in Table 2 for VeRA), both remain more versatile due to their smaller number of trainable parameters. However, the authors propose a solution to address this trade-off.

VeRA can be combined with DoRA by applying VeRA to the directional update component instead of LoRA, resulting in a method called DVoRA. While DVoRA requires slightly more parameters than VeRA, it delivers a notable improvement in accuracy when evaluated on MT-Bench( Table 2), achieving a score of 5.0 compared to VeRA’s 4.3, while adding only 0.02% more trainable parameters relative to the full model size.

Similarly, DoRA can also be combined with the quantization approach used in QLoRA. By quantizing the pretrained model and applying DoRA in place of LoRA, a method called QDoRA is introduced. When tested against QLoRA on Orca-Math, QDoRA demonstrates a substantial performance boost, outperforming QLoRA by 0.19 and 0.23 points on LLaMA2 7b and LLaMA3–8b, respectively, as seen in Table 3.

Conclusion

In this post, we have discussed DoRA[1], a fine-tuning method that builds on LoRA and improves upon it, while being closer in behavior to full fine-tuning. We have examined DoRA’s performance compared to LoRA and demonstrated that it consistently outperforms it across various tasks and model architectures. We also covered DoRA’s compatibility with other improvements over LoRA (QLoRA/VeRA).

In my opinion, DoRA proves to be a strong competitor to any LoRA-based fine-tuning method, guaranteeing better performance with fewer resources. Although DoRA is currently not as widely used as LoRA in various domains, I anticipate it will see broader adoption in the coming months.

For a more hands-on tutorial and a Python implementation of DoRA and LoRA, I recommend Sebastian Raschka’s blog post [here].

For an implementation of Quantized DoRA, I suggest checking out Answer.ai’s implementation [here].

References:

[1] S.-Y. Liu, C.-Y. Wang, H. Yin, P. Molchanov, Y.-C. F. Wang, K.-T. Cheng and M.-H. Chen, DoRA: Weight-Decomposed Low-Rank Adaptation (2024), arXiv preprint arXiv:2402.09353

[2] E. J. Hu, Y. Shen, P. Wallis, Z. Allen-Zhu, Y. Li, S. Wang, L. Wang and W. Chen, LoRA: Low-Rank Adaptation of Large Language Models (2021), arXiv preprint arXiv:2106.09685

[3] T. Dettmers, A. Pagnoni, A. Holtzman and L. Zettlemoyer, QLoRA: Efficient Finetuning of Quantized LLMs (2023), arXiv preprint arXiv:2305.14314
[4] D. J. Kopiczko, T. Blankevoort and Y. M. Asano, VeRA: Vector-based Random Matrix Adaptation (2023), arXiv preprint arXiv:2310.11454

[5] Q. Zhang, M. Chen, A. Bukharin, N. Karampatziakis, P. He, Y. Cheng, W. Chen and T. Zhao, AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning (2023), arXiv preprint arXiv:2303.10512

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI