Boost Your Fine-Tuning Performance with TPGM
Last Updated on July 17, 2023 by Editorial Team
Author(s): Denny Loevlie
Originally published on Towards AI.
Unveiling an Optimization Technique Without the Need for Extra Hyper-Parameters!
Background
At the recent CVPR 2023 conference in Vancouver, I had the privilege of exploring cutting-edge research in the field of transfer learning. Transfer learning is applicable to multiple domains, such as computer vision, natural language processing, and molecular modeling. Among the standout papers I encountered, one stood out for its innovative approach to fine-tuning and its potential to overcome existing limitations.
In the past several years, fine-tuning large models on a specific task has gained popularity due to the high accuracy that is achievable with less training and less data. It has been shown that the initial layers of the network tend to learn more general information, and the final layers are more “task specific”, therefore, we would like to retain that general information while targeting our own tasks.
Methods have been proposed based on this knowledge. For example, it would make sense to choose a different learning rate for each layer (using smaller learning rates for the first few layers and larger ones for the final ones). The downside to this is that it adds several new hyper-parameters to the problem, and thus it is not feasible when trying to train larger models on sizable datasets. This leads to a reliance on manual heuristics and time-consuming hyper-parameter searches to find optimal learning rates.
The Newly Proposed Method
In the paper “Trainable Projected Gradient Method for Robust Fine-tuning,” the authors address the issues explained above through an exciting solution termed Trainable Projected Gradient Method (TPGM) [1]. By formulating fine-tuning as a bi-level constrained optimization problem, TPGM automates the process of learning fine-grained constraints for each layer.
TPGM introduces a set of projection radii, representing distance constraints between the fine-tuned model and the pre-trained model, and enforces them using weight projections. What sets TPGM apart is its ability to “learn” these projection radii through a novel end-to-end bi-level optimization approach, eliminating the need for a manual search or slow non-derivative-based optimization techniques (e.g., grid searches). These radii are optimized based on the validation dataset, so it is important to make sure the rest of the parameters are frozen when conducting this portion of the optimization to avoid data leakage.
Normally, the loss can be described as:
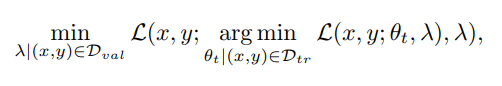
This represents the traditional way of tuning hyper-parameters in machine learning. In this case, the objective is to minimize the loss function on a validation set, where:
- (x, y) — represents a pair of input data
- L(·) — represents the task loss function
- θt — represents the trainable model weights
- λ — represents the hyper-parameters, such as the learning rate
- Dval and Dtr — represent the validation and training datasets respectively
The traditional process can be considered a bi-level optimization problem because it involves two steps. First, we adjust the hyper-parameters λ to reduce the error on the validation set, and then within this adjusted context, we tweak the model parameters θt to minimize the error on the training set.
The loss function presented in Tian et al. [1], extends this formulation for fine-tuning a pre-trained model by introducing an additional constraint. This new formulation not only minimizes the loss function as before but also ensures the distance between the fine-tuned model parameters (θt) and the pre-trained model parameters (θ0) does not exceed a predefined limit γ.
The additional parameters in this loss function include:
- γ — a scalar that represents the maximum allowed distance between the pre-trained model and the fine-tuned model
- θ0 — representing the weights of the pre-trained model
- θt-θ0 — represents the difference between the weights of the fine-tuned model and the pre-trained model, effectively measuring the ‘distance’ between them
The addition of the constraint U+007CU+007Cθt − θ0U+007CU+007C* ≤ γ aims to maintain the generalization and robustness of the fine-tuned model by ensuring it does not deviate too much from the pre-trained model (the amount of deviation allowed will be determined by the performance on the validation dataset). This forms a bi-level constrained minimization problem.
Conclusion
The authors’ experiments demonstrate that TPGM outperforms vanilla fine-tuning methods in terms of robustness to out-of-distribution (OOD) data while maintaining competitive performance on in-distribution (ID) data. For instance, when applied to datasets like DomainNetReal and ImageNet, TPGM showcases significant relative improvements in OOD performance.
To delve deeper, the unique aspects of TPGM and its implications can be better understood through the following key points:
- TPGM presents a transformative solution for fine-tuning in transfer learning.
- TPGM formulates fine-tuning as a bi-level constrained optimization problem, which aids in automating the learning of fine-grained constraints for each layer.
- TPGM alleviates the need for task specific heuristics and time consuming hyper-parameter searches.
- A key finding is that different layers require different levels of regularization. The results show that the lower layers of the neural network are more tightly constrained, indicating their closer proximity to the ideal model. This is consistent with the common understanding that lower layers tend to learn more general features.
As someone working in the field of deep learning, with previous research experience in optimization, I find this paper to be extremely impactful. The proposed method, TPGM, offers a significant leap forward in the world of transfer learning, potentially paving the way for more efficient, robust, and interpretable models in the future.
Citation
[1] Tian, J., Dai, X., Ma, C-Y., He, Z., Liu, Y-C., & Kira, Z. (2023). Trainable Projected Gradient Method for Robust Fine-tuning. In Proceedings of the Conference on Computer Vision and Pattern Recognition (pp. TBD). doi:10.48550/arXiv.2303.10720
Resources
Connect with Me!
I’m an aspiring deep-learning researcher currently working as a Computer Vision Engineer at KEF Robotics in Pittsburgh! Connect with me, and feel free to reach out to chat about anything ML related!
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Related posts
Popular posts
Updates
Recent Posts
