Be Confident in your Machine Learning Models with the help of Cross-Validation
Last Updated on August 1, 2023 by Editorial Team
Author(s): Shivamshinde
Originally published on Towards AI.
Cross-validation is a go-to tool to check if your machine-learning model is reliable enough to work on new data. This article will discuss cross-validation, from why it is needed to how to perform it on your data.
Overfitting
Evaluating the trained machine learning model on training data itself is fundamentally wrong. If done, the model will only return the values that it has learned during training. This evaluation will always give 100% accuracy and won’t give any insight into how good the trained model will be on the new data. There is a high chance that such a model will perform poorly on new data. Such a condition where the model works with high accuracy on trained data but very poorly on new data is known as overfitting.
Splitting of data into training data and testing data
Often, the data is split into two parts to counter the overfitting problem and to know the actual accuracy of the trained model. These two split parts are called training data and testing data. Testing data is smaller in size, about 10%-20 % of the original data.
The idea here is to train the data on training data and then evaluate the trained model on the testing data.
But in this approach also, there is a slight chance of overfitting. Let’s take an example of a linear support vector machine algorithm. The support vector machine algorithm has a parameter ‘C’ which is used for regularization (i.e., increasing or decreasing the constraints on the model). One can adjust the value of ‘C’ to get the high accuracy of the trained model on testing data. This, again could lead to the problem of overfitting. Such a model could work poorly in real-time after deployment into production since it has been tailored to achieve high performance on testing data in the experiment phase rather than actually improving the accuracy.
To better deal with the overfitting issue, we can split the data into three parts, namely training, validation, and test data.
Splitting the data into training, validation, and the test data
Splitting the data into three parts would prevent us from tuning the model to get high accuracy in the experimenting phase.
Training data will be the biggest part of the split (about 80% of the original data). Validation and test data will be about 10% each of the original data. Note that these percentages are just given for reference, and one can change them if they wish.
The machine learning model would be trained on the training data. The evaluation of the trained model will be performed using the validation data. And lastly, the prediction on test data will be our way to check how well the trained model will perform in real-time.
Even if one tries to tune the model so as to get high accuracy on validation data, we would know if the model trained is reliable or not with the help of its performance on testing data.
This approach also is not without disadvantages.
we are splitting the data into three parts leading to the reduction of data that could have been used for training purposes. By splitting the data, we are potentially losing 20% of the data.
Another disadvantage of this approach is that the accuracy of the model will differ based on splits that are made. It is possible that one of the splits would give very good accuracy while one of the other would give low accuracy.
The cross-validation method is used to deal with these two demerits to some extent.
Cross-validation
In cross-validation, we still need to have testing data but validation data is not needed.
First, we split the original data into training data and testing data. And then, the model is trained on training data as follows:
- Training data is split into ’n’ equal parts. Let’s name each of the splits from split 1 to split n.
- The model is trained on every group of ‘n-1’ splits possible. We will get n such groups.
- The trained model is evaluated using the remaining split for every group of (n-1) splits.
Let’s take one example to understand this more clearly.
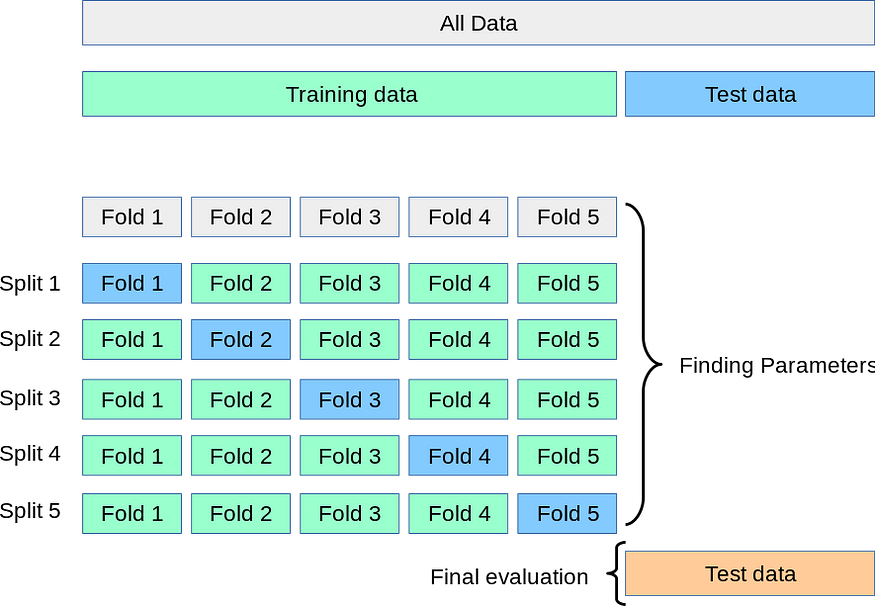
Let’s say we split the training data into 5 parts. Now, we will find out all the possible groups of 4 splits. These groups are shown in the above diagram in green color. And the last remaining split for every group of four splits is in blue color in the above diagram.
For split 1, the model is trained on the group (Fold2, Fold3, Fold4, Fold5). After training, the model is evaluated on Fold1.
For split 2, the model is trained on the group (Fold1, Fold3, Fold4, Fold5). After training, the model is evaluated on Fold2.
For split 3, the model is trained on the group (Fold1, Fold2, Fold4, Fold5). After training, the model is evaluated on Fold3.
For split 4, the model is trained on the group (Fold1, Fold2, Fold3, Fold5). After training, the model is evaluated on Fold4.
For split 5, the model is trained on the group (Fold1, Fold2, Fold3, Fold4). After training, the model is evaluated on Fold5.
Finally, we average the accuracy of all the splits to get the final accuracy. This average accuracy will be our validation performance. Since we get accuracy for each of the splits, we can obtain the standard deviation of these accuracies also.
We can then check the performance of the model trained on the parameters used in cross-validation using the test data for final evaluation. We call this accuracy test performance.
If the validation performance and the test performance of the model are good and comparable then we can consider our model reliable to use in real time.
Performing cross-validation on the data using scikit-learn’s cross_val_score method
Let’s use the iris flower dataset for the demonstration.
## Importing required libraries
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, cross_val_score, cross_val_predict
from sklearn.ensemble import RandomForestClassifier
## Performing loading
data = load_iris()
df = pd.DataFrame()
df[data.feature_names] = data.data
df['target'] = data.target
## Splitting the data into independent and dependent features
X, y = df.drop('target', axis=1), df['target']
## splitting the data into training data and testing data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
## evaluating the ranodm forest classifier model using cross validation
rfc = RandomForestClassifier(max_depth=3)
cross_validation_score = cross_val_score(rfc, X_train.values, y_train.values, cv=5, scoring = 'accuracy')
print(f"The cross validation score of the random forest classifier is {round(cross_validation_score.mean(), 2)} +/- {round(cross_validation_score.std(),2)}.")

Here, for ‘cv’ value is an integer. We can provide the value to the ‘cv’ parameter using cross-validation iterators such KFold, and StratifiedKFold.
## using cross validation iterator KFold
from sklearn.model_selection import KFold
rfc = RandomForestClassifier(max_depth=3)
kf = KFold(n_splits=5)
cross_validation_score = cross_val_score(rfc, X_train, y_train, cv=kf, scoring = 'accuracy')
print(f"The cross validation score of the random forest classifier is {round(cross_validation_score.mean(), 2)} +/- {round(cross_validation_score.std(),2)}.")

## using cross validation iterator StratifiedKFold
from sklearn.model_selection import StratifiedKFold
rfc = RandomForestClassifier(max_depth=3)
skf = StratifiedKFold(n_splits=5)
cross_validation_score = cross_val_score(rfc, X_train, y_train, cv=skf, scoring = 'accuracy')
print(f"The cross validation score of the random forest classifier is {round(cross_validation_score.mean(), 2)} +/- {round(cross_validation_score.std(),2)}.")

The data is split in equal ratios into training and testing data according to the target classes when we use the StratifiedKFold iterator.
We can even find out the predictions using the model trained while performing cross-validation.
## making predictions using cross_val_predict
from sklearn.model_selection import cross_val_predict
rfc = RandomForestClassifier(max_depth=3)
cv_predictions = cross_val_predict(rfc, X, y, cv=5)
print(f"The predictions on the test data are: {cv_predictions} (shape: {cv_predictions.shape})")

Using cross-validation with the scikit-learn pipelines
We will perform one preprocessing step on the data before training the model on the data. Let’s create a pipeline and then find the cross-validation score.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
pipe = Pipeline([
('standardization', StandardScaler()),
('model', RandomForestClassifier(max_depth=3))
])
cross_validation_score = cross_val_score(pipe, X_train, y_train, cv=5, scoring = 'accuracy')
print(f"The cross validation score of the random forest classifier is {round(cross_validation_score.mean(), 2)} +/- {round(cross_validation_score.std(),2)}.")

I hope you like the article. If you have any thoughts on the article then please let me know. Any constructive feedback is highly appreciated.
Connect with me on LinkedIn.
Have a great day!
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














