People Analytics

Author(s): Mishtert T

Originally published on Towards AI.

Better than your gut feeling

Performance Evaluation — Things to watch out for

This is a bit of a longer than usual article. If you are interested in people analytics, performance evaluation then, in my opinion, this would be worth your while.

People analytics is a data-driven approach to managing people at work. Business leaders can make decisions about their people based on an in-depth analysis of data rather than on traditional methods of personal relationships, experience-based decision-making, and risk-avoidance.

People analytics touches all people-­related issues in organizations like:

• Hiring / Assessment
• Retention
• Performance evaluation
• Learning and development
• Team composition, Etc.

Why Now?

It’s predominantly because of the technical progress that we’ve had in the last decade which has led to data availability, processing power, analytical tools, etc.

Not only the technology enablement but also there is a growing recognition of behavioral biases in the workplace and also increasingly, the recognition of the companies/firms that their greatest assets are people.

A growing recognition that greatest assets are people

Performance Evaluation

The performance evaluations predominantly exist for two reasons:

• Feedback
• Rewards/punishment

The primary challenge is that it is tough to compare employees if not in identical situations.

There is noise in the performance measures (i.e) outcomes are imperfectly related to employee effort. The challenge is to separate skill from luck.

To understand this better, let’s begin by assuming that all employees have equal skills/capability.

For any given level of effort, a range of outcomes can occur due to factors outside the employee’s control (Competitors, team members, her boss, etc)

The challenge is to separate skill from luck.

In some places, it’s easier to do this

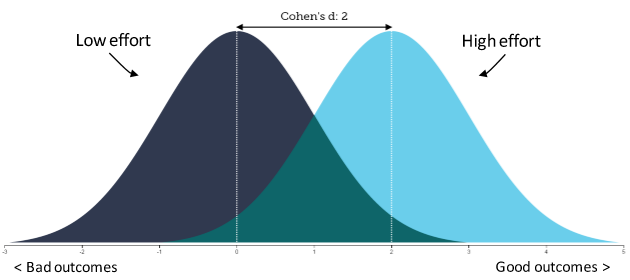
In some, it’s not so easy.

Simple Model

Now how can we understand if it’s performance or if it’s luck?

There are two components to performance, Real Ability + Luck, in other words, it can be expressed formally as y = x(true ability) + e (error) . error, randomly distributed around zero.

What does this mean for when we’re sampling extreme performance? What is the foundation of serious success and failure?

• Extreme success = f(x); x = (superior ability, positive error)
• Extreme failure = f(x); x = (inferior ability, negative error)

Extreme success suggests that the person might have a superior ability or tried very hard but also that they got lucky. (The error was positive.)

And, on the other hand, extreme failure may mean inferior ability, or that they did not try very hard, (the error was negative), or that they were unlucky.

So what are the consequences of that? There’s one very important consequence. That is, in subsequent periods, errors won’t be negative again. It will regress to the mean. You’d expect it to be zero.

Error is by definition zero. And if you’ve got a very positive error in one period, you would expect less error in the following period. This is a notion called regression to the mean and it’s one of the most important
notions in performance evaluation

Regression To Mean:

Anytime we sample based on extreme values of one attribute, any other attribute that is not perfectly related will tend to be closer to the mean value.

They can be:

• Performance at different points in time — E.g., stock returns year over year
• Different qualities within the same entity — E.g., a person’s cycling speed, and learning ability

Example (Points to Ponder)

There was a study a few years ago about mutual fund performance in the 1990s. There were 283 funds in this study. The study divided the 1990s into two parts, the first half to be 1990–1994 and then from1995–1999 the second half.

They looked at the top ten performing funds from the first half of the decade and their performance in the early 1990s. , these are only the top-10 performing funds. (Fig. A)

Then they went out and asked how would these funds perform in subsequent years,

So here are the predictions, the estimations, from the people that they asked.

We can see that they didn’t expect the firms to be as good, but they expected some regression to the mean. (Fig. B)

It was clear that those funds were not expected to remain in their current position but were estimated to move with an average ranking of 25.

Then they looked at what actually happened. What actually happened?

It ranged from 129th, 21st, 54th. Interestingly their rank average was 142.5.

What is the significance of 142.5? It’s half of the total number of firms in the study.

In other words, the average performance of the top 10 firms in the second half of the ’90s, was perfectly average for this sample. They regressed entirely.

If that’s the case, what does that say about how much skill versus luck was involved in how those firms did, in the first half of the ‘90s? The regression of the rank average to the mean in the second period, suggests that there was no skill.

Regression Toward the Mean: An Introduction with Examples

Regression to the mean is a common statistical phenomenon that can mislead us when we observe the world. Learning to…

fs.blog

Why is this regression-to-mean a hard concept to understand and to live by?

Outcome Bias:

Well, there are a few things that get in the way. Among others, we have this outcome bias.

We tend to believe that good things happen to people who worked hard. Bad things happen to people that worked badly. And on that basis, we draw an inference too powerful. We start to judge decisions and people by outcomes and not by process.

This is a real and significant problem and it gets in the way of our understanding of this concept, regression to the mean framework for the world.

Hindsight Bias:

Next is hindsight bias. Once we’ve seen something occur we have a hard time accepting to believe that that we did not expect it to happen. We, in fact, often misbelieve that we anticipated that that’s exactly what would happen.

We show hindsight bias and again, if that’s the way we reason about what happens, then we’re not gonna appreciate that what happens next could
possibly be just regression to the mean.

Narrative Seeking:

We want to make sense of the world, we want to connect the dots, we came to believe things better we can tell a causal story between what took place at time one and what took place at time two. And if we can tell a causal story, then we actually have great confidence in our ability to predict what happens next.

We seek stories. And that again gets in the way of our understanding of the statistical processes that actually drive what’s going on.

So, in short, we make sense of the past. We are sense-making animals and
we make sense of the past. And there’s not a lot of sense to be had for
mere regression to the mean, but it’s going to get in our way of
predicting what happens next.

We try to find stories that connect all the dots. And by doing so, we give too small a part to chance in those stories.

Sometimes, we connect the dots based on our knowledge gained over the years, and adding some experience to that knowledge helps us draw those lines, but sometimes we are inclined to overfit those lines and we turn what should be a pretty straight grid, pretty parsimonious connections into something that will probably replicate in the future.

It might be a very satisfying interpretation of the past but it is overfitting, and an overfit interpretation of the past is going to make very bad predictions about the future.

Sample Size

Let’s now talk about sample size and let’s begin with the psychology of sample size to motivate our use of data to increase samples and provide some caution on our use of small intuitive samples.

A quick example. This is from classic research where participants were asked the following.

Your organization has two plants, one small and one large, which manufactures a standard computer chip. The two plants are similar in all respects other than the quantity they produce. Under normal circumstances, this technology produces 1% defective items. A special note is made in the quality control log, whenever the number of defective items from a day’s production exceeds 2%. Which plant would you expect to have more flagged days in the quality control log at quarter-end?

Usually ~20% say the smaller plant, ~30% say it’s the larger plant, and then about half say the same. Because in fact, Since all the technologies are essentially the same, why would they be any different?

What’s the right answer? The right answer is, of course, the small plant. Because you get more variation from the small samples and what we’re talking about here is variation.

These are outcomes of production which fall outside the limits of expected quality control. Those are variations from expectations. Small samples often are more varied and people don’t appreciate that.

And this is a major problem for performance evaluation because we are inclined to draw a conclusion, too strong, from small samples.

Looking at this in more detail, the sample means converge to the population
means as the sample size increases (Central Limit Theorem).

An example question. What about hospitals? Where are you likely to see a dramatically higher proportion of boys born on any given day than girls, or vice versa? A small community hospital, maybe having 4–5 births a day? Or a large hospital in the town that could have 100 births a day. Where are you more likely to see the mean of the population vary in that daily sample?

Of course, the small hospital could see great variations. You might even have all-girls in a small hospital one day, all-boys another day. It’s highly unlikely you have that in a larger hospital.

We tend to believe that what is seen in a small sample is representative of the underlying population. We do not appreciate a small sample being able to bounce around quite a bit. And not, in fact, be representative of the population that it underlies.

This means that we should be very careful to not follow our intuition about what it means when we only have a small sample.

The law of small numbers literature acknowledges this bias. In fact, what makes the small numbers interesting is that there is no law, they bounce around.

People believe small samples share closely the properties of the underlying population, but in fact, they don’t. This means the population’s properties are too readily inferred, the average from the samples. The role of variability, the role of the chance, is neglected in these small samples.

The learning is, almost always get more data, get bigger samples, be careful about the inferences drawn from small numbers and know that we have a bias towards jumping too quickly based on the small samples.

Signal Independence:

Forecasts average of a large group reliably outperforms the average individual forecast.

An example. In historical county fairs, where you might have a large cow, in a pen. The weight of the cow can be guessed by everyone who comes to the fair. And the fascinating bit is that even though most peoples guesses are quite wrong, the average of their guesses is remarkably accurate.

And this has not been shown only in county fairs, but also in many other domains that the result of all these bets is that the idiosyncratic areas offset each other. I might guess a little bit high, you might guess a little bit low. If there’s enough of you and me making these guesses, then we tend to get very close to the truth.

Getting more inputs provides a way to get closer to the truth by getting more signals, getting more people involved, getting more judgments from more people. This is something that more firms should do more of.

But there’s one very important caveat.

The value of the crowd depends critically on how independent their opinions are.

So if, for example, in the county fair if everyone who takes a guess at the weight of the cow talked with each other before they made their guess, the value of the crowd would greatly diminish.

Those idiosyncratic errors would be a little bit less idiosyncratic. They’d be related to each other. One person who was loudly arguing that he knew because of what breed of a cow this was, or the last cow he saw, that this was a particular weight, he would influence everybody’s opinion.

Their opinions would no longer be independent and would wash away the value of these independent signals

So, it’s not only a crowd that you need. You need a crowd that independent of one another to a possible extent. Independent here means uncorrelated. If the opinions are correlated, then the value of each additional opinions quickly diminishes.

If you have the opinion of 100 people, if they’re highly correlated, then you might only have the opinion of 5 or 10.

Bob Clemen and Bob Winkler at Duke, 1985 did a study where they kind of worked out mathematically, the equivalent number of experts for a given number of experts and the degree to which those experts are correlated

Here’s what they found. If the correlation is 0, that is to say, if the experts are completely independent, then every expert you add creates equivalent new value.

When those expert opinions become correlated even at 0.2, we quickly lose the value of adding experts.

So for example, in the above chart, it shows that as you go from 0 experts to 9, if you have a correlation of 0.2, you never quite get above 4.

While we push towards more opinions, more assessments, we’ve got to simultaneously try to maintain the independence of those opinions.

Now, where does the correlation come from? How can we think about signal
independence in terms that we are familiar with with-in the organizations?

Well, the most obvious thing about that is, it happens when people discuss the issue together. When they’ve had conversations. When they’ve bounced their
ideas, opinions off of each other. As soon as that’s happened, they no longer have independent opinions.

It can happen when they just speak to the same people. They may not speak to each other but they both speak to the same third party. Or they share the same friends, or they went to dinner on different nights before. All of these things break independence, all of these things increase correlation.

It even happens when people have the same background. If they’re from the same place. If they’ve trained the same way. If they have the same advisors, mentors, teachers. If they have the same kind of experiences. All of these things tend to increase the correlation in their opinions.

Therefore, all of these things break down the independence and decrease the value of adding additional voices to whatever process we’re running.

Get more voices, as much as we can. Design processes to keep these voices as independent as possible.

Outcome vs. Process:

An organization or individual ought to consider a broader set of objectives than they typically consider for decision-making/evaluation.

So for example, perhaps most importantly, what effect did that employee have on other employees along the way of achieving any result? What impact did they have on others? Can we get that kind of information into the performance evaluation as well

We need to measure more things. This is validated by the research by Bond, Carlson, and Keeney. It was found that people considered too few objectives.

Generating Objectives: Can Decision Makers Articulate What They Want?

Objectives have long been considered a basis for sound decision making. This research examines the ability of decision…

pubsonline.informs.org

Summary of the research is that if you ask people what they’re trying to accomplish. They’ll list a few objectives. They ask a large group and then you share all the possible answers with people who originally listed objectives, they will go back and say, oh yeah, I forgot that. They had listed on their own only about half of all the objectives they ultimately recognize as relevant.

This study shows that we may not be good at focusing on the right measures or objectives to evaluate the performance or for decision making although we think we know what we want.

In general, the more the uncertainty in an environment, the less control an employee has over the exact outcomes, the more a firm should emphasize process over outcome.

So if there’s more noise, the less control the employee has on outcome, the more they should be evaluated on the process and not on outcome. We can try to overcome this by using analytics to find out which processes tend to produce the desired outcomes.

And what are you looking for here is the most fundamental driver of the outcome? It could be that only the last step in the process is measured when in fact, there are some intermediate steps that may be more important and fundamental, and they could provide additional performance measures.

A hockey example to illustrate the point in the discussion.

For a long time, teams & players were evaluated, based on goals and if you were trying to figure out whether a team was really good they’d look at the number of goals they had been scoring/scored. If they wanted to evaluate
if a player was weak or strong, the contribution of the player to the goals scored while he was on the ice was looked at.

But can we do better? It turns out there are not many goals scored in hockey. And sometimes goals are scored because they hit the pole and went left and goals were not scored because they hit the pole and went right.

There is a lot of noise between what actually happens and what a player can control.

And whenever there’s that noise we have to be careful about how much weight we put on it. It’s not giving us a very reliable signal for the true effort, or the true ability underneath it.

So what did they do? They determined that shots were a better predictor than goals through analytics. If you looked at how many shots that were hit, at the net. That was a better predictor and a more reliable measure.

And when you think about it, it’s more persistent across games and during a game. A player, or a team that looks good in one period on shots, is more likely to look good in the next period than a player who looks good on goals in the earlier period vs. the next. It’s a more persistent and more fundamental measure.

Subsequently, it was realized what really matters is possession, it’s not even shots. There’s again so much noise on shots that what the best measure they can find on team or player’s contribution to possession.

The teams that keep that puck, are the ones that are most likely to shoot. more the shoots, most likely the goals. But they had to figure that out going backward-looking for the more and more fundamental measure, and you can think of these as process measures. They had to get away from the noisy, outcome measure of a goal, to the more fundamental, process-oriented, and more reliable measure, possession.

Comparing this to our business world, can a sales organization come up with more fundamental measures than the traditional dollars booked? Can you, for example, consider the process that leads to those dollars booked?

Should the number of bids that a salesperson gets her organization into looked at? Or maybe before that, Is it the relationship-building he does to get offers to book the dollars? Or maybe even it’s earlier than that. It’s an earlier process yet. It’s the number of contacts generated, we have to determine exactly which of these would be most persistent.

It will vary by organization and by industry, but the idea is to take data to the problem and determine where in the process we might start adding assessments to get away from these relatively, rare noisy outcome measures at the very least to complement them with more fundamental drivers earlier in the process.

Summary:

We need to ask ourselves these questions that are below when we are doing performance evaluation and also need to understand a few of the key areas that we saw above.

How much is my environment, or how much is the environment of the employees that we’re evaluating, like a math problem, and how much of it is like a lottery?

We also need to understand that we’re biased. If we don’t understand regression to the mean, we’ll forecast too directly from things that have happened in the past. We generally assume that the outcomes reflect the underlying efforts or quality with this Outcome bias.

We tend to believe that we knew something was gonna happen before it happened, even though we didn’t, this is Hindsight bias.

And we have the habit of building narratives that make sense of all the events that we observe. All of these things limit our appreciation for the role that chance plays.

And finally, some critical questions.

1. Are the differences persistent or random?
2. How do we know that this isn’t just good or bad luck?
3. Are samples large enough to draw strong conclusions?
4. How can we make the sample larger?
5. How many different signals are we really looking at here?
6. How can we make samples, assessments, voices as independent as possible?
7. What else do we care about?
8. Are we measuring enough?
9. Is there a more fundamental measure that’s available than what we’re measuring right now?

The key is persistence, large samples, independent assessments, and more fundamental measures, more process measures. we can take these critical
questions to any evaluation and improve the decision-making process.

Inspired by lectures of The Wharton School on people analytics.

Published by Towards AI.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI