Make Art with Math. Become an Artist

Author(s): Mishtert T

Originally published on Towards AI.

Phyllotaxis

Not only Analysis… R can make beautiful things too…

“Mathematics is the science of patterns, and nature exploits just about every pattern that there is. ” (Ian Stewart)

Phyllotaxy

The arrangement of leaves on a plant stem is called phyllotaxis or phyllotaxy in botany. A distinctive class of patterns in nature are the phyllotactic spirals.

Let’s see how a nice example of how mathematics can create patterns in nature.

Nature & Pattern

Many natural facts can be described in mathematical terms.

Examples: Shape of snowflakes, the fractal geometry of romanesco broccoli or how self-similarity rules the growth of plants.

R is a tool for doing serious analysis, but R can be used to have fun and to do beautiful things. The graphical power of R can be used to produce artistic images too.

R Package: ggplot2

Warm-up: Points on a circle

For this illustration, we will use “ggplot 2” package from R to draw the flower.

We will work with geom_point()which plots points in two dimensions (Scatterplot). We’ll create a dataset with two variables, which will be called “x” and “y”.

We’ll draw a circle with a radius of 1 and 50 points on the circle.

The Pythagorean trigonometric identity which states that sin²(θ) + cos²(θ) = 1 for any real number θ will help us to achieve this.

Since we need every (x, y) point in the unit circle, it should follow x² + y² = 1.

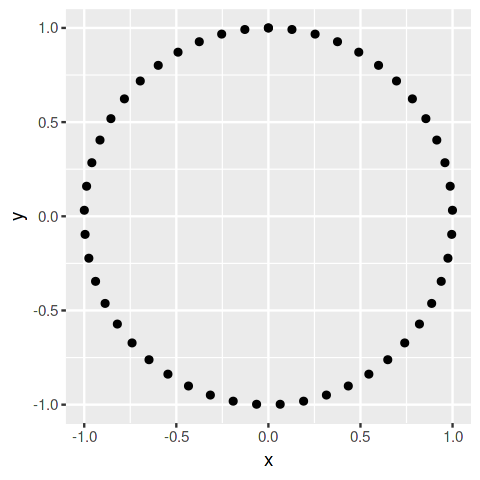
t <- seq(0, 2*pi, length.out = 50)
x <- sin(t)
y <- cos(t)
df <- data.frame(t, x, y)

# Make a scatter plot of points in a circle
p <- ggplot(df, aes(x, y))
p + geom_point()

Harmonization with Golden Angle

Arranging leaves in a spiral. A spiral is a curve which starts from the origin and moves away from this point as it revolves around it.

All points in the above plot are the same distance from the origin. To arrange them spirally, multiply x and y by a factor which increases for each point.

We will use Golden Angle to make it look much more harmonious.

Golden Angle = π(3 − √5)

This number is inspired by the Golden Ratio, one of the most famous numbers in the history of mathematics.

Imagine that you have a circumference and you break up it into two arcs with lengths a and b, with a and b (an arc is a portion of the circumference).

The angle that breaks the circle so that a/b=(a+b)/a is called the Golden Angle.

In other words: the Golden Angle breaks a circle so that the ratio of the big arc to the little arc is the Golden Ratio.

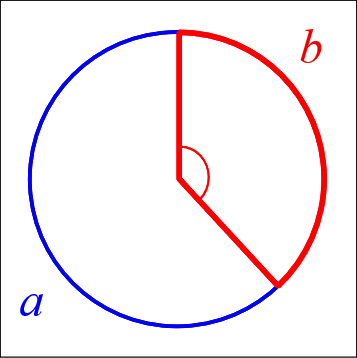
The angle subtended by the smaller (red) arc is called the Golden Angle.

In unexpected places in nature, both the Golden Angle and the Golden Ratio appear. Flower petals, leaves of trees and plants, heads of seeds, pine cones, seeds of sunflower, shells, hurricanes, etc.

Start Drawing Spirals

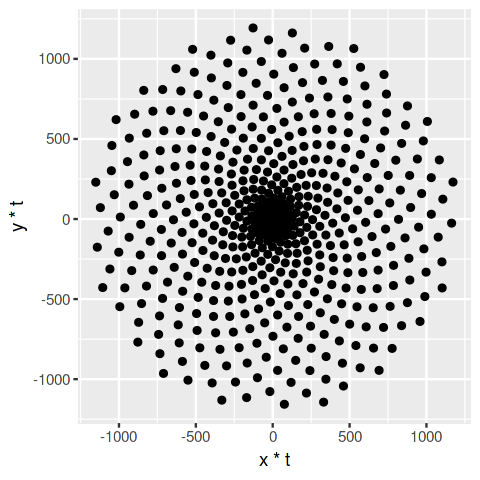
# Defining the number of points
points <- 500# Defining the Golden Angle
angle <- pi * (3 -sqrt(5))t <- (1:points) * angle
x <- sin(t)
y <-cos(t)
df <- data.frame(t, x, y)# Make a scatter plot of points in a spiral
p <- ggplot(df, aes(x*t, y*t))
p + geom_point()

Keeping it Simple

To get the plot to look artsier, let’s remove distracting items from the plot.

1. Background with grey color.
2. Grid of horizontal and vertical white lines.
3. Ticks along the axis.
4. Title on each axis.
5. Text along axes to label marks

df <- data.frame(t, x, y)# Make a scatter plot of points in a spiral
p <- ggplot(df, aes(x*t, y*t))p + geom_point() + theme(legend.position="none",panel.background = element_rect(fill = "white"),panel.grid=element_blank(),axis.ticks=element_blank(),axis.title=element_blank(),axis.text=element_blank())

Now that distractions have been removed, let’s try and get them to look a little beautiful.

Let’s see what happens when we change color, transparency (also called alpha, and size of the points.

# Modify the size, transparency, and color of the points
p <- ggplot(df, aes(x*t, y*t))
p + geom_point(size = 8, alpha = 0.5, color = "darkgreen") + theme(legend.position="none",panel.background = element_rect(fill = "white"),panel.grid=element_blank(),axis.ticks=element_blank(),axis.title=element_blank(),axis.text=element_blank())

Dandelion

If you notice, all the points have the same appearance. The size, color, shape, and alpha all are the same.

Sometimes you will want to make the appearance of the points dependent on a variable in your dataset.

Here, we will make the “size” variable. We will also change the shape of the points.

Are you reminded of a dandelion when you look at the below image?

p <- ggplot(df, aes(x*t, y*t))
p + geom_point(aes(size = t), shape = 8 ) +
theme(legend.position="none", panel.background = element_rect(fill = "white"),panel.grid=element_blank(),axis.ticks=element_blank(),axis.title=element_blank(),axis.text=element_blank())

Getting it all together: Sunflower

Not only do plants use the Golden Angle to arrange leaves. It is also used in the sunflower seed arrangement.

We just need to mix some of the stuff that we already know to create a sunflower.

p <- ggplot(df, aes(x*t, y*t))
p + geom_point(aes(size = t), shape = 17,color = "yellow" ) +
theme(legend.position="none",panel.background = element_rect(fill = "darkmagenta"),panel.grid=element_blank(),axis.ticks=element_blank(),axis.title=element_blank(),axis.text=element_blank())

Will something change if we modify the angle?

angle <- 2.0
points <- 1000t <- (1:points)*angle
x <- sin(t)
y <- cos(t)
df <- data.frame(t, x, y)# Copy the plotting code from Task 7
p <- ggplot(df, aes(x*t, y*t))
p + geom_point(aes(size = t), shape = 8,color = "yellow" ) +
theme(legend.position="none",panel.background = element_rect(fill = "darkmagenta"),panel.grid=element_blank(),axis.ticks=element_blank(),axis.title=element_blank(),axis.text=element_blank()

Where is the flower?

Now that we know how to play around with points, angles, and colors let’s see what we can create just by changing the shape and color

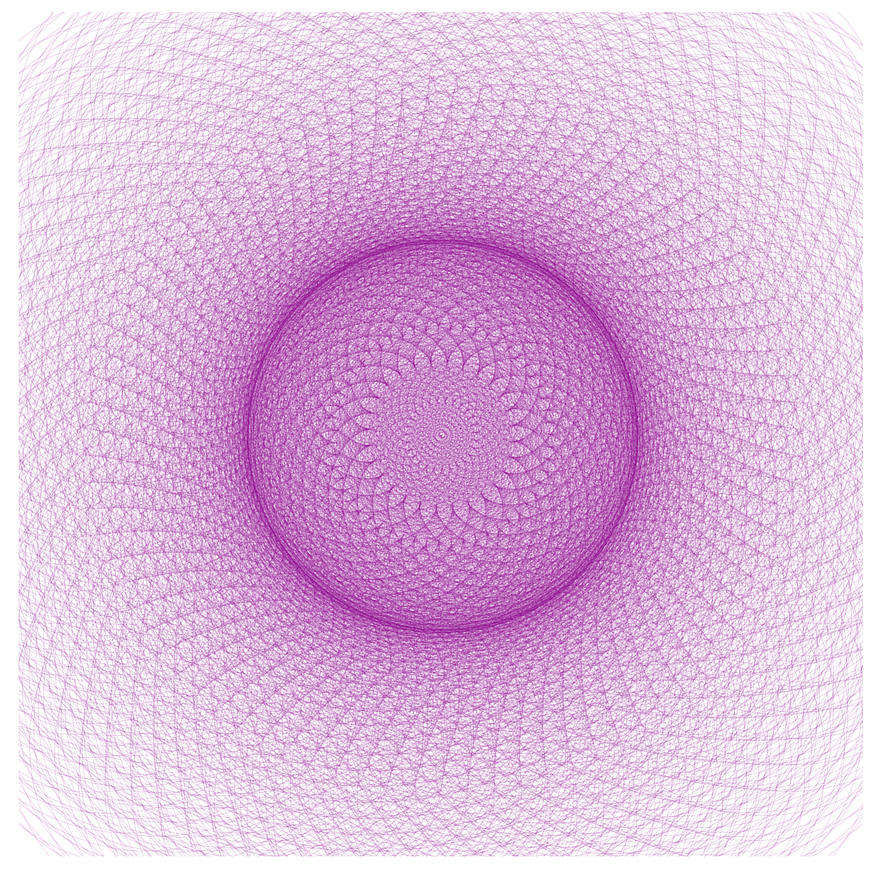
The picture on the left is a simple variant of the previous flower and is very similar to the first figure in which we plotted 50 points in a circle.

I hope you’ve enjoyed the journey between that simple circle and this beautiful flower

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI