Centroid Neural Network: An Efficient and Stable Clustering Algorithm
Last Updated on August 19, 2021 by Editorial Team
Author(s): LA Tran
Deep Learning
Let’s upraise potentials that are not paid much attention
Generally, clustering is grouping multi-dimensional datasets into closely related groups. Classical representatives of clustering algorithms are K-means Clustering and Self-Organizing Map (SOM). You can easily find numerous resources for those algorithm explanations. This time, let me introduce to all of you another efficient clustering algorithm but seemingly no many researchers pay attention: Centroid Neural Network for Unsupervised Competitive Learning. Please click here to have a closer looking at the original paper.

And now, let’s get started!
Centroid Neural Network (CentNN)
To avoid confusion with Convolution Neural Network, I would like to use the term “CentNN” in this post.
CentNN is an unsupervised competitive learning algorithm based on the classical k-means clustering algorithm that estimates centroids of the related cluster groups in training date. CentNN requires neither a predetermined schedule for learning coefficient nor a total number of iterations for clustering. In the paper, the simulation results on clustering problems and image compression problems show that CentNN converges much faster than conventional algorithms with compatible clustering quality while other algorithms may give unstable results depending on the initial values of the learning coefficient and the total number of iterations.

The above figure shows the CentNN algorithm. If you get bored when looking at all those mathematical equations, don’t worry, I am going to make it more understandable with a secondary-school-maths example.
Weight Update
The core of the algorithm is the weight update procedure: How to calculate efficiently the centroid of a group of data points when a single data point moves in or out?
For instance, we have 100 integers, it’s very simple to calculate the mean value by averaging all of them. Then what happens if we have one more integer? Do we need to average all 101 those ones again? The answer is NO!
Let’s say we have N and N+1 data points, the mean value w is calculated as follows:
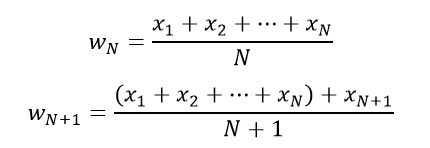
From the 2 above equations:
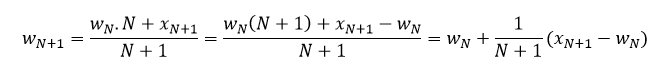
Now we can calculate the mean of 101 integers without averaging all of them again. It’s similar when we move out one integer to have 99 integers.
And the example above explains these equations in the paper:
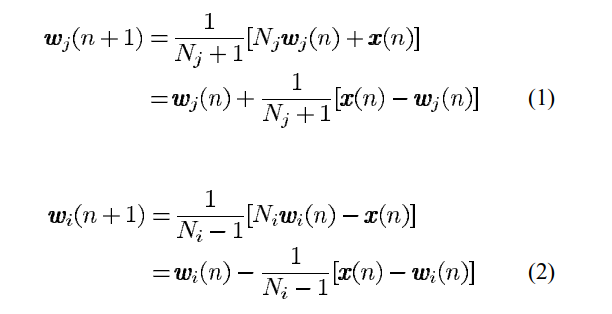
Visual Explanation Example
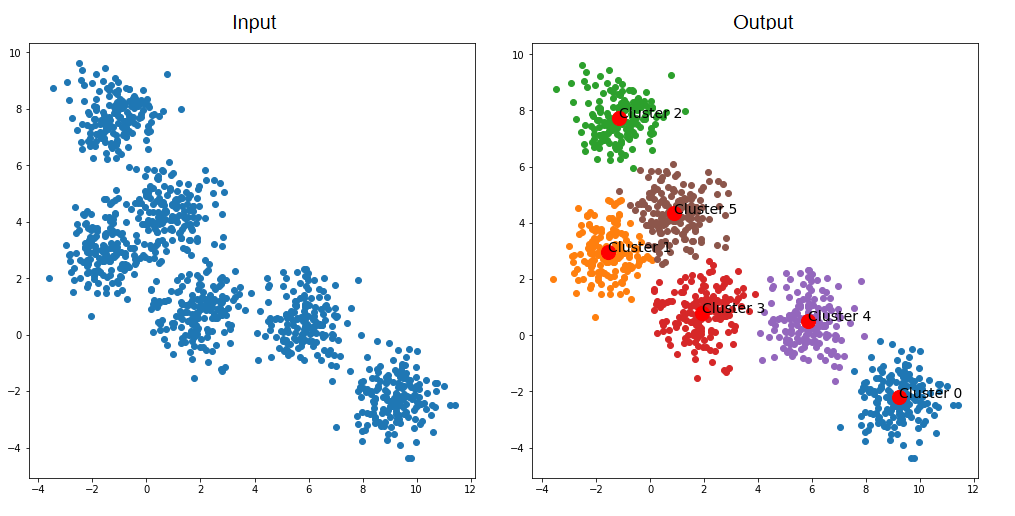
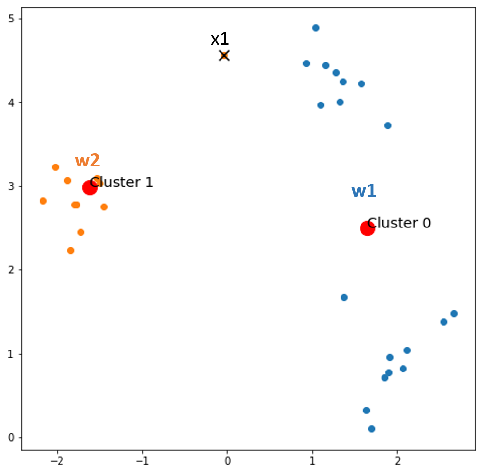
Given a dataset with 30 data points as the figure below, our aim is to cluster them into 3 clusters.
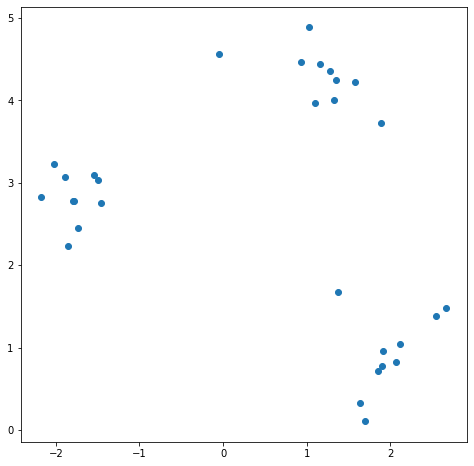
Epoch 0: Initialization
Find 1 centroid c for all data, then split c into 2 weights w1, w2 with a small Ɛ.
w1 = c + Ɛ, w2 = c — Ɛ (e.g. Ɛ = 0.05 )
Before going ahead, let’s talk about the term “winner neuron” and “loser neuron”.
- winner neuron: input a data x, the winner neuron is the weight (w) which is closest to x among all weights.
- loser neuron: input a data x at epoch n, if in epoch (n-1), w was the closest weight to x, but in epoch n, there is another weight w’ which is closer to x than w, then w is a loser neuron and w’ is a winner neuron for the data x at epoch n.
Find the winner neuron for each x in X.
- x1 comes, w1 wins → update w1
- x2 comes, w2 wins → update w2
- x3 comes, w1 wins → update w1
- …
- x30 comes, w1 wins → update w1
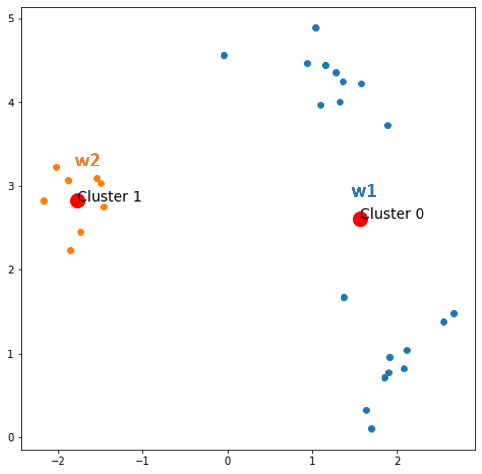
After epoch 0, we always have 2 centroids and information of clustered data points. Now, keep it here:
- x1 comes, w1 wins
- x2 comes, w2 wins
- x3 comes, w1 wins
- …
- x30 comes, w1 wins
Epoch 1:
Find the winner neuron for each x in X.
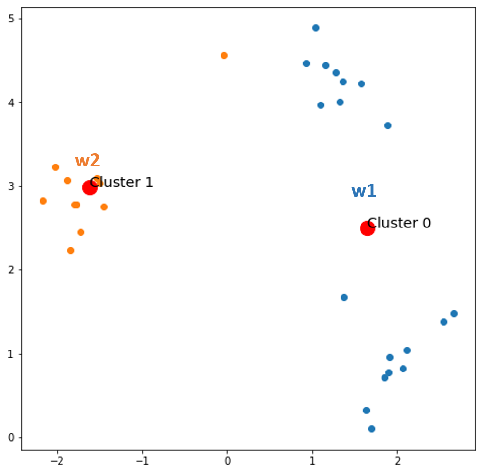
- x1 comes, w2 wins → w1 loses, loser += 1, update weights.
- x2 comes, w2 wins
- x3 comes, w1 wins
- …
- x30 comes, w1 wins
After epoch 1, we have 1 data whose cluster is updated, and the number of loser neurons increases by 1. By looking, we can still realize that x1 is closer to w2 rather than w1, but at epoch 0, x1 was clustered to w1, now it is updated correctly. Again, keep the information here:
- x1 comes, w2 wins
- x2 comes, w2 wins
- x3 comes, w1 wins
- …
- x30 comes, w1 wins
Epoch 2:
Keep finding the winner neuron for each x in X.
- x1 comes, w2 wins
- x2 comes, w2 wins
- x3 comes, w1 wins
- …
- x30 comes, w1 wins
Now, nothing changes. Let’s check if the number of clusters now reaches the desired number of not. The answer is NOT YET. Then we start splitting the centroid with the most error with a small Ɛ.
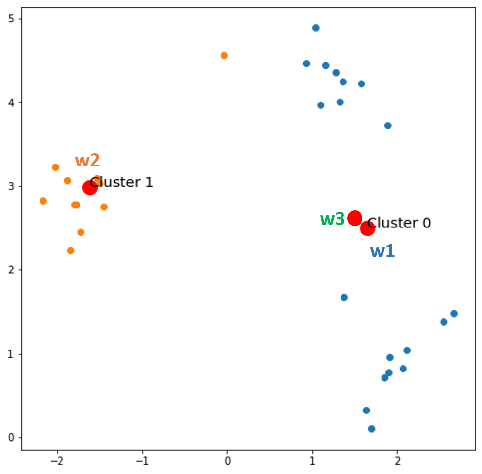
Now do the same procedure from epoch 1.
Epoch 3:
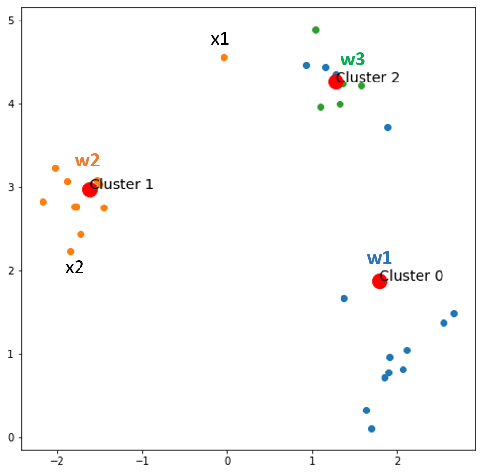
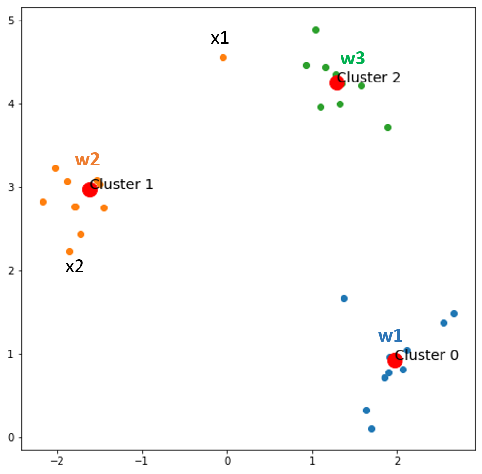
Epoch 4:
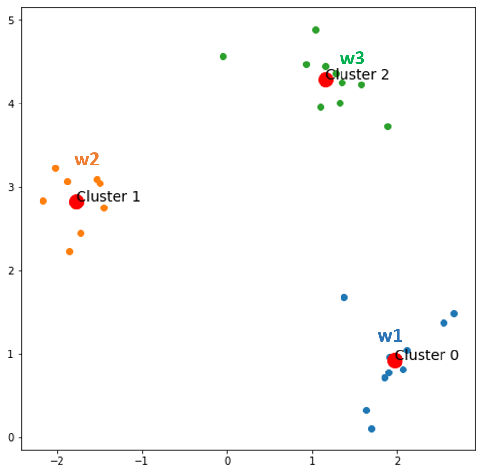
Epoch 5:

Now, nothing changes, and we also reach the desired num of clusters. Now, time to party!

Below is the comparison between the results of K-Means Clustering and CentNN in image compression. We can see that CentNN outperforms K-Means Clustering in terms of PSNR (peak signal-to-noise ratio), with PSNR 47.53 compared to PSNR 46.35, respectively. In the example, the image size is 128×128, the number of clusters is 48.

CentNN Implementation
You guys can find my implementation of CentNN in Python here. If you feel it helps, please do not hesitate to give it a star.
By the way, you are welcome to visit my Facebook page which is for sharing things regarding Machine Learning: Diving Into Machine Learning.
In this post, I have introduced to all of you Centroid Neural Network (CentNN), an efficient clustering algorithm. The main feature of CentNN is that it updates weights every time a single new data comes, while K-means Clustering updates centroids after every iteration.
In order to avoid the algorithm from getting stuck at an undesirable local minimum solution, CentNN starts with setting the number of groups to two and increases the number of groups one by one until it reaches the predetermined number of groups. The CentNN algorithm does not provide any guarantee of convergence to the global minimum solution like other unsupervised algorithms but does provide a guarantee of convergence to a local minimum.
Centroid Neural Network: An Efficient and Stable Clustering Algorithm was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.
Published via Towards AI

 Logo:
Logo:  Areas Served:
Areas Served: